2021-2022初中数学九年级上册期末测试卷（含答案） (3)

这是一份2021-2022初中数学九年级上册期末测试卷（含答案） (3)，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
答卷前，请考生务必将自己的姓名、准考证号、座号、考试科目涂写在答题卡上，并同时将考点、姓名、准考证号、座号填写在试卷规定的位置．考试结束后，将试卷、答题卡一并交回．本考试不允许使用计算器．
第I卷（选择题 共48分）
注意事项：
第Ⅰ卷为选择题，每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号．答案写在试卷上无效．
一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）
1．cs60°的值等于
A. B. C. D. 1
2．已知反比例函数y＝的图象经过点（2，－2），则k的值为
A．4 B．－4C．－2 D．－
3. 如图是将正方体切去一个角后形成的几何体，则该几何体的左视图为
3题图
4. 一个不透明的布袋中，放有3个白球，5个红球，它们除颜色外完全相同，从中随机摸取1个，摸到红球的概率是
A． B． C． D．
5. 关于x的一元二次方程 (m－1)x2－2x－1＝0有两个实数根，则实数m的取值范围是
A．m≥0 B．m≥0且m≠1 C．m＞0 D．m＞0且m≠1
6. 已知在Rt△ABC中，∠C=90°，sinA=，则tanB的值为
A． B． C． D．
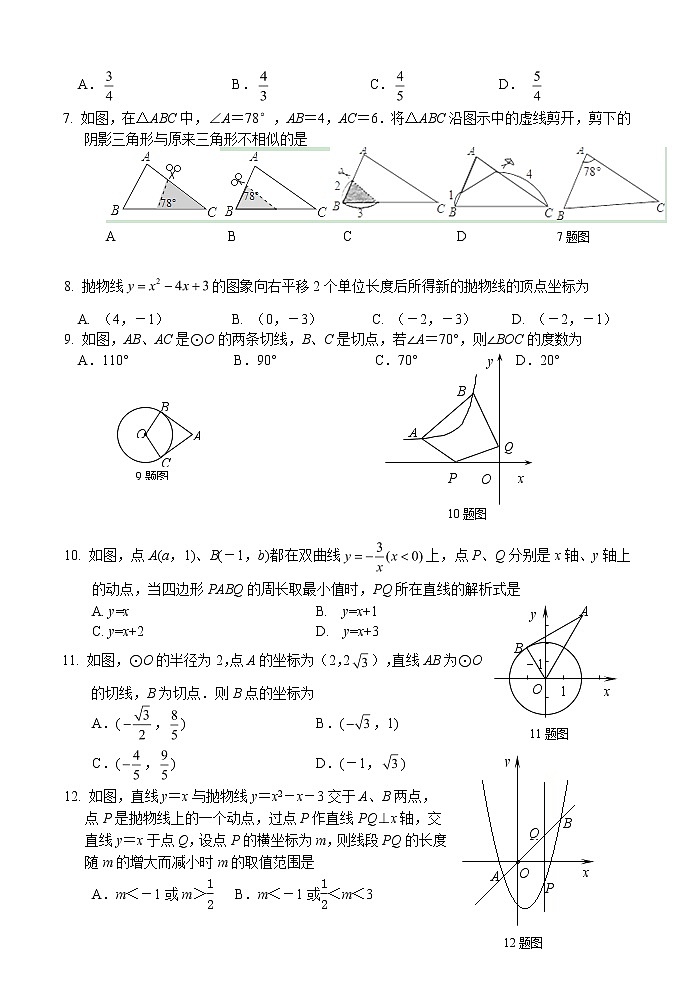
7. 如图，在△ABC中，∠A＝78°，AB＝4，AC＝6．将△ABC沿图示中的虚线剪开，剪下的阴影三角形与原来三角形不相似的是
A B C D 7题图
8. 抛物线的图象向右平移2个单位长度后所得新的抛物线的顶点坐标为
A. （4，－1） B. （0，－3） C. （－2，－3） D. （－2，－1）
9. 如图，AB、AC是⊙O的两条切线，B、C是切点，若∠A＝70°，则∠BOC的度数为
A
B
O
y
x
P
10题图
Q
A．110° B．90° C．70° D．20°
A
9题图
B
C
O
10. 如图，点A(a，1)、B(－1，b)都在双曲线上，点P、Q分别是x轴、y轴上的动点，当四边形PABQ的周长取最小值时，PQ所在直线的解析式是
x
y
O
1
－1
B
A
11题图
A. y=x B. y=x+1
C. y=x+2 D. y=x+3
11. 如图，⊙O的半径为2，点A的坐标为（2，2），直线AB为⊙O
的切线，B为切点．则B点的坐标为
A．(，) B．(，1)
A
B
y
x
O
P
Q
12题图
C．(，) D．(－1，)
12. 如图，直线y＝x与抛物线y＝x2－x－3交于A、B两点，
点P是抛物线上的一个动点，过点P作直线PQ⊥x轴，交
直线y＝x于点Q，设点P的横坐标为m，则线段PQ的长度
随m的增大而减小时m的取值范围是
A．m＜－1或m＞ EQ \F(1,2) B．m＜－1或 EQ \F(1,2)＜m＜3
C．m＜－1或m＞3 D．m＜－1或1＜m＜3
第Ⅱ卷（非选择题 共102分）
注意事项：
所有答案必须用0.5毫米的黑色签字笔(不得使用铅笔和圆珠笔)写在答题卡各题目指定区域内（超出方框无效），不能写在试卷上，不能使用涂改液、修正带等.
不按以上要求做答，答案无效.
二、填空题(本大题共6个小题．每小题4分，共24分．把答案填在答题卡的横线上.)
13．关于x的一元二次方程(k－1)x2+6x+k2－k=0的一个根是0，则k的值是 ．
14．如图所示，把一个长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置，若
∠EFB＝65°，则∠AED′等于 度.
15．如图，在平行四边形ABCD中，E为AD的中点，△DEF的面积为1，则△BCF的面
积为 .
E
D
B
C′
F
C
D′
A
14题图
A
B
C
D
E
F
G
P
16题图
A
B
C
D
E
F
15题图
16．如图，在菱形ABCD和菱形BEFG中，点A、B、E在同一直线上，P是线段DF的中点，
连接PG、PC．若∠ABC=∠BEF=60°，则的值为__________.
17．如图所示，△ABC的三个顶点的坐标分别为A(－1，3)、B (－2，－2)、C (4，－2)，则
△ABC外接圆半径的长度为 ．
x
y
O
A
B
C
18题图
D
A
B
C
O
x
17题图
y
18．如图，反比例函数y=的图象经过点（－1，－2），点A是该图象第一象限分支上一动点，连接AO并延长交另一分支于点B，以AB为斜边作等腰直角三角形ABC，顶点C在第四象限，AC与x轴交于点D.当时，则点C的坐标为 .
三、解答题(本大题共9个小题，共78分．解答应写出文字说明，证明过程或演算步骤.)
19．(本小题满分6分)
解方程：
20．(本小题满分6分)
如图，在⊙O中，OC⊥AB于点C，AB=4，OC=1，求⊙O的半径.
20题图
21．(本小题满分6分)
21题图
如图，在平面直角坐标系xOy中，一次函数y＝3x＋2的图象与y轴交于点A，与反比例函数y＝(k≠0)在第一象限内的图象交于点B，且点B的横坐标为1．过点A作AC⊥y轴交反比例函数y＝(k≠0)的图象于点C，连接BC．
(1)求反比例函数的表达式．
(2)求△ABC的面积．
22．(本小题满分8分)
设方程的两个根为x1、x2，令，，若点P的横坐标和纵坐标为x1、x2、m、n这四个数中任意两个数，则点P落在第二象限的概率是多少？
23．(本小题满分8分)
如图，正方形ABCD中，M为BC上一点，F是AM的中点，EF⊥AM，垂足为F，交AD的延长线于点E，交DC于点N．
(1)求证：△ABM∽△EFA；
(2)若AB=12，BM=5，求DE的长．
24．(本小题满分10分)
已知：如图，在△ABC中，AC=BC，以BC为直径的⊙O与边AB相交于点D，DE⊥AC，垂足为点E.
O
A
B
D
C
E
24题图
(1)求证：点D是AB的中点；
(2)求证：DE是⊙O的切线；
(3)若⊙O的直径为18，csB =，求DE的长.
25. (本小题满分10分)
(1)如图1，△ABC中，∠C=90°，∠ABC=30°，AC=m，延长CB至点D，使BD=AB.
①求∠D的度数；
②求tan75°的值.
(2)如图2，点M的坐标为(2，0)，直线MN与y轴的正半轴交于点N，∠OMN=75°.
x
O
M
N
25题图2
y
求直线MN的函数表达式.
A
B
C
D
25题图1
26．(本小题满分12分)
如图，点B的坐标是(4，4)，作BA⊥x轴于点A，作BC⊥y轴于点C，反比例函数(k＞0)的图象经过BC的中点E，与AB交于点F，分别连接OE、CF，OE与CF交于点M，连接AM.
(1)求反比例函数的函数解析式及点F的坐标；
(2)你认为线段OE与CF有何位置关系？请说明你的理由.
y
O
A
B
C
E
F
M
x
26题图
(3)求证：AM=AO.
27．(本小题满分12分)
已知一次函数与抛物线交于A(0，1)，B两点，B点纵坐标为10，抛物线的顶点为C.
(1)求b，c的值；
(2)判断△ABC的形状并说明理由；
(3)点D、E分别为线段AB、BC上任意一点，连接CD，取CD的中点F，连接AF，EF.当四边形ADEF为平行四边形时，求平行四边形ADEF的周长.
B
A
O
C
D
E
F
x
y
27题图
九年级数学试题参考答案与评分标准
一、选择题：
二、填空题：
13. 0 14. 50 15. 4 16. 17. 18. (2，－)
三、解答题：
19.解:∵，
∴2x2－7x+3=01分
∴a=2，b=－7，c=32分
∴b2－4ac=253分
∴4分
∴6分
20.解：⑴连接OA，2分
∵OC⊥AB于点C，AB=4，
∴AC=BC=2，4分
在Rt△AOC中：
∵OC=1 ，AC =2
由勾股定理得：6分
21. 解：(1)∵点B在一次函数y＝3x＋2的图象上，且点B的横坐标为1，
∴y＝3×1＋2＝5，
∴点B的坐标为(1，5)．1分
∵点B在反比例函数的图象上，
∴，
∴k＝5，
∴反比例函数的表达式为．2分
（2）∵一次函数y＝3x＋2的图象与y轴交于点A，
∴当x＝0时y＝2，
∴点A的坐标为(0，2)．3分
∵AC⊥y轴，
∴点C的纵坐标为2，
∵点C在反比例函数的图象上，
∴当y＝2时，，x＝，
∴AC＝．4分
过点B作BD⊥AC于点D，
∴BD＝yB－yC＝5－2＝3，5分
∴S△ABC＝＝＝．6分
22.解：，
，，1分
∴，2分
，3分
将点P可能的坐标情况列表如下
6分
点P落在第二象限内共有（－1，3）（，3）（，3）三种情况，7分
∴点P（落在第二象限）==.8分
23. (1)证明：∵四边形ABCD是正方形，
∴AB=AD，∠B=90°，AD∥BC，1分
∴∠AMB=∠EAF，2分
又∵EF⊥AM，
∴∠AFE=90°，
∴∠B=∠AFE，3分
∴△ABM∽△EFA；4分
(2)解：∵∠B=90°，AB=12，BM=5，
∴AM==13，AD=12，5分
∵F是AM的中点，
∴AF=AM=6.5，
∵△ABM∽△EFA，
∴,即6分
∴AE=16.9，7分
∴DE=AE－AD=4.9．8分
24. (1)证明：连接CD
则CD，1分
又∵AC = BC，
∴AD = BD，
∴点D是AB的中点．2分
(2)证明：连接OD3分
则DO是△ABC的中位线
∴DO∥AC4分
又∵DE
∴DE
即DE是⊙O的切线.5分
(3)∵AC = BC，
∴∠B =∠A， 6分
∴cs∠B = cs∠A =，7分
∵ cs∠B =，BC = 18，
∴BD = 6，
∴AD = 6，8分
∵ cs∠A =，
∴AE = 2，9分
在Rt△AED中，DE=10分
25. (1)①∵BD=AB，
∴∠D=∠BAD，1分
∴∠ABC=∠D+∠BAD=2∠D=30°，2分
∴∠D=15°.3分
②∵∠C=90°，
∴∠CAD=90°－∠D=90°－15°=75°，4分
∵∠ABC=30°，AC=m，
∴BD=AB=2m，BC=， 5分
∴CD=CB+BD=，6分
∴tan∠CAD==2+，
∴tan75°=2+.7分
⑵∵点M的坐标为(2，0)，∠OMN=75°，∠MON=90°，
∴ON=OM·tan∠OMN =2×(2+)=，
∴点N的坐标为(0，)，8分
设直线MN的函数表达式为，
则9分
解得，
∴直线MN的函数表达式为.10分
26. 解：(1)∵BC⊥y轴，BA⊥x轴，∠AOB=90°，
∴四边形ABCO是矩形，1分
∵点B的坐标是(4，4)，点E是BC中点，
∴BC=BA=4，
∴点E的坐标为(2，4)，点F的横坐标为4，2分
∴将点E的坐标代入得：，
解得：，
即反比例函数的函数解析式为，3分
∴点F的坐标为(4，2).4分
(2)OE⊥CF.5分
由(1)知四边形ABCO是正方形，CE=2， BF=2，
∴BC=OC，∠B=∠OCE=90°，BF=CE，
∴△BCF≌△COE，6分
∴∠BCF=∠COE，7分
∴∠COE+∠OCM=∠BCF+∠OCM=∠OCE=90°，
∴OE⊥CF.8分
(3) 延长CF交x轴于点G，9分
∵∠B=∠FAG=90°，FB=FA，∠BFC=∠AFG，
∴△BFC≌△AFG，10分
∴BC=AG，
∴AG=AO，11分
∴MA是直角三角形OMG斜边上的中线，
∴AM=OG=AO.12分
27. 解：(1)把A（0，1），代入
得1分
将代入，得，
∴B点坐标为，2分
将B ，代入
得3分
(2)△ABC是直角三角形4分
∵
∴点C的坐标为(－3，－2)5分
分别作BG垂直于y轴，CH垂直于y轴6分
∵ ，
∴°
同理°
∴°
∴△ABC是直角三角形7分
27题图
O
A
B
C
D
E
F
G
H
y
x
(3)∵ ，
∴，
∵，
∴，8分
∵，
∴∥EF，
又∵，
∴，9分
即EF为△DBC的中位线，
∴
∵，
∴10分
在Rt△，
∴11分
∵，
∴
∴平行四边形ADEF周长为.12分
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
B
C
D
B
B
C
A
A
C
D
D
横坐标
纵坐标
－1
3
－1

（3，－1）
（，－1）
（，－1）
3
（－1，3）

（，3）
（，3）
（－1，）
（3，）

（，）
（－1，）
（3，）
（，）