2021-2022初中数学九年级上册期末测试卷（含答案） (6)

这是一份2021-2022初中数学九年级上册期末测试卷（含答案） (6)，共7页。试卷主要包含了01，答题必须用0，下列说法等内容，欢迎下载使用。
注意事项:
1.本试卷由填空题、选择题和解答题三大题组成，共28题，满分130分.考试用时120
分钟.
2.答题前，考生务必将学校、姓名、考场号、座位号、考试号填写在答题卷相应的位置上.
3.答题必须用0.5mm黑色墨水签字笔写在答题卷指定的位置上，不在答题区域内的答案
一律无效，不得用其他笔答题.
4.考生答题必须在答题卷上，答在试卷和草稿纸上一律无效.
一、选择题(本大题共10小题，每小题3分，共30分.请将下列各题唯一正确的选项代号填涂
在答题卡相应的位置上)
1.方程的解是( )
A. B. C. D.
2.数据1, 3, 3, 4, 5的众数和中位数分别为( )
A. 3和3 B. 3和3.5 C. 4和4 D. 5和3.5
3.己知⊙的半径为5cm，点是线段的中点，当=8cm时，点与⊙的位置关系
是( )
A.点在⊙外 B.点在⊙上 C.点在⊙内 D.不能确定
4.在中，，则的外接圆的半径为( )
A. 3 B. 6 C. 7.5 D. 15
5.在平面直角坐标系中，二次函数与坐标轴交点个数( )
A. 3个 B. 2个 C. 1个 D. 0个
6.下列说法:①三点确定一个圆;②任何三角形有且只有一个内切圆;③相等的圆心角所对的弧
相等;④正多边形一定是中心对称图形，其中真命题有( )
A. 1个 B. 2个 C. 3个 D. 4个
7.将抛物线先向上平移3个单位长度，再向右平移1个单位长度可得抛物线
( )
A. B.
C. D.
8. 中，，其内切圆半径为1，则的周长为( )
A. 15 B. 14 C. 13 D. 12
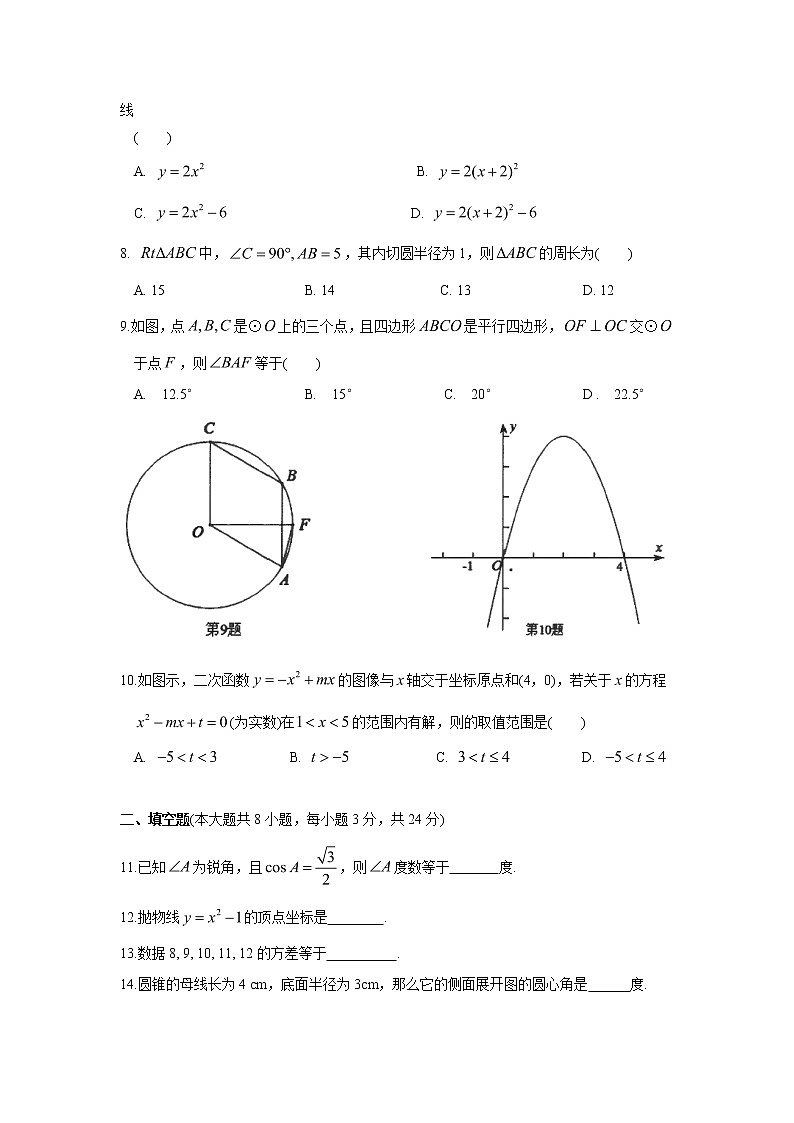
9.如图，点是⊙上的三个点，且四边形是平行四边形，交⊙
于点，则等于( )
A. 12.5° B. 15° C. 20° D . 22.5°
10.如图示，二次函数的图像与轴交于坐标原点和(4，0)，若关于的方程
(为实数)在的范围内有解，则的取值范围是( )
A. B. C. D.
二、填空题(本大题共8小题，每小题3分，共24分)
11.已知为锐角，且，则度数等于 度.
12.抛物线的顶点坐标是 .
13.数据8, 9, 10, 11, 12的方差等于 .
14.圆锥的母线长为4 cm，底面半径为3cm，那么它的侧面展开图的圆心角是 度.
15.已知二次函数的自变量与函数的部分对应值列表如下:
则关于的方程的解是 .
16.如图示，半圆的直径是半圆上的三等分点，点是的中点，则阴影部
分面积等于
17.如图示，在边长为1的小正方形网格中，点都在这些小正方形的顶点上，
和相交于点，则= .
18.如图示，在中，，点在内部，且
，连接，则的最小值等于 .
三、解答题(本大题共10小题，共76分.应写出必要的计算过程、推理步骤或文字说明)
19.计算(本题满分共8分，每小题4分)
(1) (2)

20.(本题满分5分) 解方程:
21.(本题满分5分)
如图示，在中，，求的面积.
22.(本题满分6分)快乐的寒假即将来临小明、小丽和小芳三名同学打算各自随机选择到A, B
两个书店做志愿者服务活动.
(1)求小明、小丽2名同学选择不同书店服务的概率;(请用列表法或树状图求解)
(2)求三名同学在同一书店参加志愿服务活动的概率.(请用列表法或树状图求解)
23.(本题满分6分)根据龙湾风景区
的旅游信息，某公司组织一批员
工到该风景区旅游，支付给旅行
社28000元.你能确定参加这次
旅游的人数吗?
24.(本题满分8分)己知函数(是常数)
(1)当=1时，该函数图像与直线有几个公共点?请说明理由;
(2)若函数图像与轴只有一公共点，求的值.
25.(本题满分8分)如图，利用135°的墙角修建一个梯形的储料场，其中,
并使，新建墙上预留一长为1米的门.如果新建墙总长为
15米，那么怎样修建才能使储料场的面积最大?最大面积多少平方米?
26.(本题满分8分)
(1)如图①，点在⊙上，点在⊙外，比较与的大小，并说明理由;
(2)如图②，点在⊙上，点在⊙内，比较与的大小，并说明理由;
(3)利用上述两题解答获得的经验，解决如下问题:
在平面直角坐标系中，如图③，已知点，点在轴上，试求当
度数最大时点的坐标.
27.(本题满分10分)如图示，是⊙的直径，点是半圆上的一动点(不与重合)，
弦平分，过点作交射线于点.
(1)求证: 与⊙相切:
(2)若，求长;
(3)若长记为,长记为，求与之间的函数关系式，并求出
的最大值.
28.(本题满分12分)如图示，在平面直角坐标系中，二次函数交轴于
，在轴上有一点，连接.
(1)求二次函数的表达式;
(2)点是第二象限内的点抛物线上一动点
①求面积最大值并写出此时点的坐标;
②若，求此时点坐标;
(3)连接，点是线段上的动点.连接，把线段绕着点顺时针旋转90°
至，点是点的对应点.当动点从点运动到点，则动点所经过的路
径长等于 (直接写出答案)