2021年中考一轮复习数学专题——反比例函数（Word版 含答案）

这是一份2021年中考一轮复习数学专题——反比例函数（Word版 含答案），共25页。试卷主要包含了单选题，四象限内，则点在，解答题等内容，欢迎下载使用。
2021年中考专题复习——反比例函数
一、单选题
1．如图过原点的直线与反比例函数图象交于M，N两点，则线段MN的长度的最小值为（ ）

A．2 B． C． D．5
2．反比例函数图象上有三个点，，，则，，的大小关系是（ ）
A． B． C． D．
3．反比例函数的图像在第二、四象限内，则点在（ ）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
4．反比例函数，当x＞0时，y随x的增大而减小，那么m的取值范围是（　　）
A．m＜3 B．m＞3 C．m＜﹣3 D．m＞﹣3
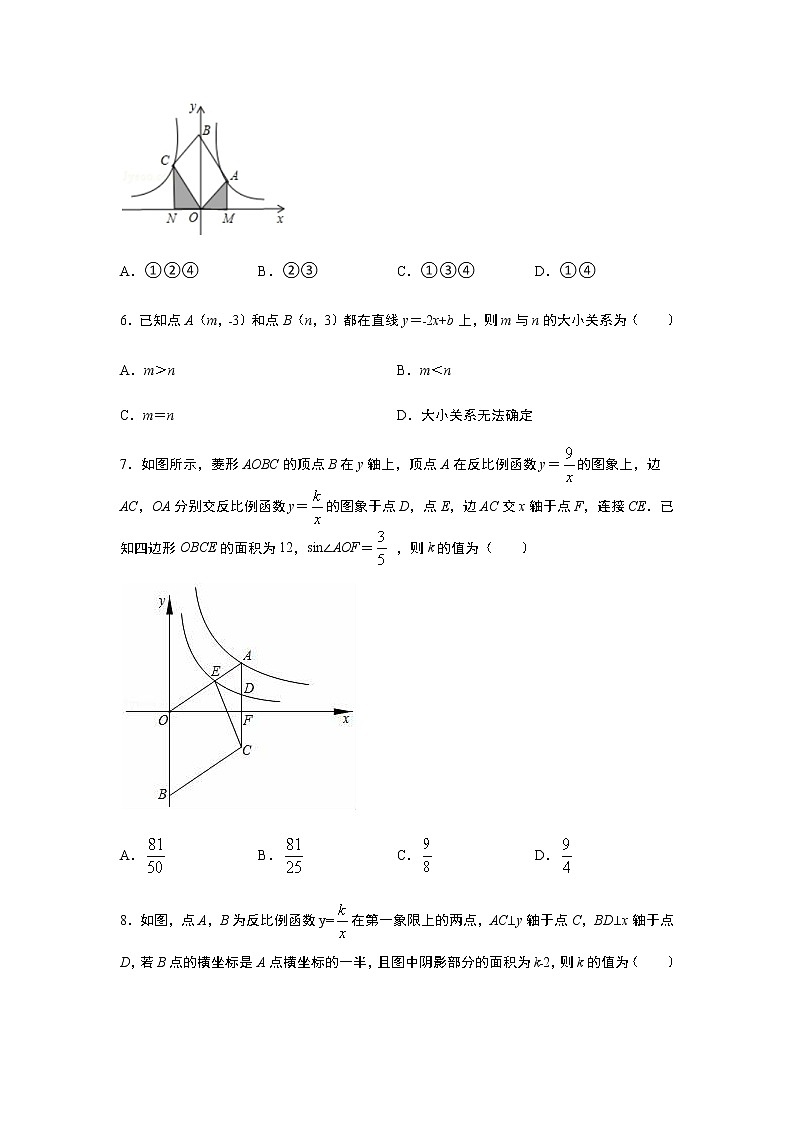
5．如图，四边形OABC是平行四边形，对角线OB在y轴上，位于第一象限的点A和第二象限的点C分别在双曲线y＝和y＝的一支上，分别过点A，C作x轴的垂线垂足分别为M和N，则有以下的结论：①ON＝OM；②△OMA≌△ONC；③阴影部分面积是（k1+k2）；④四边形OABC是菱形，则图中曲线关于y轴对称其中正确的结论是（ ）

A．①②④ B．②③ C．①③④ D．①④
6．已知点A（m，﹣3）和点B（n，3）都在直线y＝﹣2x+b上，则m与n的大小关系为（　　）
A．m＞n B．m＜n
C．m＝n D．大小关系无法确定
7．如图所示，菱形AOBC的顶点B在y轴上，顶点A在反比例函数y＝的图象上，边AC，OA分别交反比例函数y＝的图象于点D，点E，边AC交x轴于点F，连接CE．已知四边形OBCE的面积为12，sin∠AOF＝ ，则k的值为（　　）

A． B． C． D．
8．如图，点A，B为反比例函数y=在第一象限上的两点，AC⊥y轴于点C，BD⊥x轴于点D，若B点的横坐标是A点横坐标的一半，且图中阴影部分的面积为k﹣2，则k的值为（　　）

A． B． C． D．
9．如图，在平面直角坐标系中，函数y＝kx与的图象交于A，B两点，过A作y轴的垂线，交函数(x>0)的图象于点C，连接BC，则△ABC的面积为( )

A．1 B．2 C．3 D．4
10．如图，直角坐标系中，A是反比例函数y＝（x＞0）图象上一点，B是y轴正半轴上一点，以OA，AB为邻边作▱ABCO．若点C及BC中点D都在反比例函数y＝（k＜0，x＜0）图象上，则k的值为（　　）

A．﹣3 B．﹣4 C．﹣6 D．﹣8
二、填空题
11．反比例函数的图象经过点（﹣3，2），则k的值是_____．当x大于0时，y随x的增大而_____．（填增大或减小）
12．矩形的面积是，设它的一边长为（单位：），则矩形的另一边长（单位：）与的函数关系是__________．
13．如图，直线与轴交于点，与轴交于点，点在轴的正半轴上，，过点作轴交直线于点，若反比例函数的图象经过点，则的值为_________________．

14．如图，直角三角形的直角顶点在坐标原点，，若点在反比例函数的图象上，则经过点的反比例函数解析式为___；

15．如图，点A的坐标为（﹣1，0），AB⊥x轴，∠AOB＝60°，点B在双曲线l上，将△AOB绕点B顺时针旋转90°得到△CDB，则点D_____双曲线l上（填“在”或“不在”）．

16．已知点A（﹣1，y1），B（﹣2，y2）和C（3，y3）都在反比例函数y＝（k＜0）的图象上，则y1，y2，y3的大小关系为_____．（用“＜”连接）
17．已知正比例函数y＝2x的图象与反比例函数y＝（k≠0）的图象相交于A（2，m），B两点，则点B的坐标为_____．
18．如图，矩形OABC的边OA，OC分别在x轴、y轴上，点B在第一象限，点B的坐标为（12,6），反比例函数的图象分别交边BC、AB于点D、E，连结DE，ΔDEF与ΔDEB关于直线DE对称．当点F正好落在边OA上时，则k的值为________．

19．如图，已知点A在反比例函数 的图象上，作，边BC在x轴上，点D为斜边AC的中点，连结DB并延长交y轴于点E，若的面积为6，则k=___．

20．如图,已知…是轴上的点，且…，分别过点…作轴的垂线交反比例函数的图象于点…,过点作于点,过点作于点……记的面积为,的面积为……的面积为，则…等于_________．

三、解答题
21．如图，正比例函数的图象与反比例函数（k≠0）在第一象限的图象交于A点，过A点作x轴的垂线，垂足为M，已知△OAM的面积为1．
（1）求反比例函数的解析式；
（2）如果B为反比例函数在第一象限图象上的点，且B点的横坐标为1，在x轴上求一点P，使PA+PB最小．（只需在图中作出点B，P，保留痕迹，不必写出理由）

22．如图，在平面直角坐标系中，点A（0，4）、B（﹣3，0），将线段AB沿x轴正方向平移n个单位得到菱形ABCD．
（1）画出菱形ABCD，并直接写出n的值及点D的坐标；
（2）已知反比例函数y＝的图象经过点D，▱ABMN的顶点M在y轴上，N在y＝的图象上，求点M的坐标；
（3）若点A、C、D到某直线l的距离都相等，直接写出满足条件的直线解析式．

23．如图，直线y＝mx与反比例函数（x＞0）的图象交于Q点，点B（3，4）在反比例函数的图象上，过点B作PB∥x轴交OQ于点P，过点P作PA∥y轴交反比例函数图象于点A．
（1）若点A的纵坐标为，求反比例函数及直线OP的解析式；
（2）连接OB，在（1）的条件下，求sin∠BOP的值．

24．如图，直线AB经过A(，0)和B(0，1)，点C在反比例函数y＝的图象上，且AC＝BC＝AB．
(1)求直线AB和反比例函数的解析式；
(2)点D坐标为(2，0)过点D作PD⊥x轴，当△PAD与△OAB相似时，P点是否在(1)中反比例函数图象上？如果在，求出P点坐标；如果不在，请说明理由．

25．已知直线与直线y2＝kx+b关于原点O对称，若反比例函数的图象与直线y2＝kx+b交于A、B两点，点A横坐标为1，点B纵坐标为．
（1）求k，b的值；
（2）结合图象，当时，求自变量x的取值范围．
26．如图，可以自由转动的转盘被平均分成了三等分标有数字﹣2，3，﹣1的扇形区域转动转盘，待转盘自动停止后，指针指向一个扇形的内部，则该扇形内的数字即为转出的数字，此时，称为转动转盘一次（若指针指向两个扇形的交线，则不计转动的次数，重新转动转盘，直到指针指向一个扇形的内部为止）
（1）转动转盘一次，求转出的数字是3的概率；
（2）转动转盘两次，设第一次得到的数字为x，第二次得到的数字为y，点M的坐标为（x，y），请用树状图或列表法求点M在反比例函数y＝﹣的图象上的概率．

27．如图，正方形ABCD的边BC在y轴上，点D的坐标为（2，3），反比例函数y＝的图象经过点A，交边CD于点N，过点M（t，0），作直线EM垂直于x轴，交双曲线于点E，交直线AB于点F．
（1）求反比例函数的解析式；
（2）当t＝6时，求四边形ADFE的面积；
（3）当以A、D、E、F为顶点的四边形是平行四边形，求t的值．

28．如图，在平面直角坐标系xOy中，矩形OABC的顶点A在x轴上，顶点C在y轴上，D是BC的中点，过点D的反比例函数图象交AB于E点，连接DE，若OD＝5，OC＝3．
（1）求过点D的反比例函数的解析式及DE所在直线的函数解析式；
（2）设直线DE与x轴和y轴的交点分别为M、N，求△CMN的面积．

29．如图，一次函数的图象与y轴交于C(0，8)，且与反比例函数y=(x＞0)的图象在第一象限内交于A(3，a)，B(1，b)两点.
⑴求△AOC的面积；
⑵若=4，求反比例函数和一次函数的解析式.

30．如图，已知二次函数y=ax2+2x+c（a＞0）图象的顶点M在反比例函数上，且与x轴交于AB两点．
（1）若二次函数的对称轴为，试求a，c的值；
（2）在（1）的条件下求AB的长；
（3）若二次函数的对称轴与x轴的交点为N，当NO+MN取最小值时，试求二次函数的解析式．






答案
1．B
2．C
3．C
4．B
5．D
6．A
7．B
8．B
9．C
10．C
11．﹣6 增大
12．
13．24
14．
15．不在
16．y3＜y2＜y1
17．（﹣2，﹣4）
18．27； 对称的性质、相似三角形的判定与性质等知识点，解题的关键是求出F点的坐标.
19．12
20．
21．解：（1）设A点的坐标为（a，b），则由，得ab＝2＝k，
∴反比例函数的解析式为；
（2）由条件知：两函数的交点为，
解得：，
∴A点坐标为：（2，1），作出关于A点x轴对称点C点，连接BC，P点即是所求，
则点C（2，﹣1），
∵B（1，2），
设直线BC的解析式为：y＝kx+b，
，
解得：，
∴直线BC的解析式为：y＝﹣3x+5，
当y＝0时，x＝，
∴点P（，0）．

22．解：（1）如图，

∵点A（0，4）、B（﹣3，0），
∴AO＝4，BO＝3，
∴AB＝＝5，
∵四边形ABCD是菱形，
∴AB＝BC＝CD＝AD＝5，
∵将线段AB沿x轴正方向平移n个单位得到菱形ABCD，
∴n＝5，点C坐标为（2，0），点D坐标为（5，4）；
（2）∵反比例函数y＝的图象经过点D，
∴k＝4×5＝20，
∵N在y＝的图象上，
∴设点N（a，），
如图，过点N作NH⊥OA于点H，

∵四边形ABMN是平行四边形
∴AN＝BM，AN∥BM，
∴∠BMA＝∠NAM，
∴∠BMO＝∠NAH，且AN＝BM，∠BOM＝∠NHA＝90°，
∴△ANH≌△MBO（AAS），
∴HN＝BO＝3，MO＝AH，
∴HN＝a＝3，HO＝，
∴OM＝AH＝HO﹣AO＝，
∴点M（0，）；
（3）∵点A、C、D到某直线l的距离都相等，
∴直线l是△ACD的中位线所在直线，
如图所示：

若直线l过线段AC，CD中点，
∴直线l的解析式为：y＝2，
若直线l过线段AD，AC中点，即直线l过点（，4），点（1，2），
设直线l的解析式为：y＝mx+n
∴ ，
解得：m＝，n＝，
∴直线l的解析式为：y＝，
若直线l过线段AD，CD中点，即直线l过点（，4），点（，2），
设直线l解析式为：y＝kx+b
∴，
解得：k＝﹣2，b＝9，
∴直线l的解析式为：y＝﹣2x+9.
23．（1）∵B（3，4）在上的图象上，
∴
∴k＝12，
∴
当 时，
∴
∵PA∥y 轴，PB∥x 轴，
∴
将P点代入y＝mx，得
∴
∴
（2）如图，过 B 点作 BM⊥OP 于点 M，
∵B（3，4），
∴


在 Rt△BOM中，
又∵

∴

24．（1）设直线AB的解析式为y＝k'x+b，
将点A(，0)和B(0，1)代入y＝k'x+b中，得，
解得，，
∴直线AB的解析式为y＝﹣x+1，
∵A(，0)和B(0，1)，
∴OA＝，OB＝1，AB＝＝2，
∵AC＝AB＝2，
在Rt△AOB中，tan∠OAB＝，
∴∠OAB＝30°，
∵AC＝BC＝AB，
∴△ABC是等边三角形，
∴∠BAC＝60°，
∴∠OAC＝∠OAB+∠BAC＝90°，
∴AC⊥x轴，
∴C(，2)，
将点C坐标代入y＝中，得k＝2×＝2，
∴反比例函数解析式为y＝；
（2）由(1)知，OA＝，OB＝1，
∵点D坐标为(2，0)，
∴OD＝2，
∴AD＝OD﹣OA＝，
∵PD⊥x轴，
∴∠ADP＝90°＝∠AOB，
∵当△PAD与△OAB相似时，
∴①当△ADP∽△AOB时，，
∴，
∴DP＝1，
∴P(2，1)，
当x＝2时，y＝1，
∴点P(2，1)，在反比例函数解析式为y＝上；
②当△ADP∽△BOA时，
∴，
∴，
∴DP＝3，
∴P(2，3)，
当x＝2时，y＝1≠3，
∴点P(2，3)，不在反比例函数解析式为y＝上．
25．解：（1）∵，
∴当x＝0，解得，
∴当y＝0，解得x＝﹣5
∴与两坐标轴的交点为：，（﹣5，0），
∵与y2＝kx+b关于原点对称，
∴y2＝kx+b经过点：，（5，0），
∴得到方程组：，
解得：；
（2）∵点A、B在直线上
∴把x＝1代入上式解得y＝﹣2
∴A（1，﹣2）
∴把代入上式解得x＝4
∴，
∵经过点A、B，且图象关于原点成中心对称，
∴必经过点（﹣1，2）、,
且（﹣1，2）、两点即为与两个交点，

∴结合图象，当y＜y1时，x的取值范围的取值范围为：﹣4＜x＜﹣1或x＞0．
26．解：（1）转动一次有三种可能，出现数字3只有一种情况，
∴出现数字3的概率为；
（2）可能结果共9种，点M（x，y）在反比例函数y＝﹣的图象上，
只有（﹣2，3）、（3，﹣2）满足，
∴点M在反比例函数y＝﹣的图象上的概率为；

27．（1）∵正方形ABCD中，D（2，3），
∴CO＝3，CD＝AB＝2，
∵BC＝2，OB＝1，
∴A（2，1），
因为反比例函数：y＝，
∴k＝2 即y＝；
（2）t＝6时，y＝，
∴E的坐标是（6，），F的坐标是（6，1），
∴EF＝，AD＝2，
S＝×4×2+×4×＝；
（3）∵M（t，0）直线EM垂直于x轴，交双曲线于点E，交直线AB于点F，
∴E（t，），F（t，1），
∴EF＝1﹣或EF＝﹣1，
∵以A、D、E、F为顶点的四边形是平行四边形，
∴EF＝AD，即1﹣＝2 或﹣1＝2，
解得：t＝﹣2，或t＝．
28．（1）∵OD＝5，OC＝3，
∴由勾股定理得CD＝4，
∴D点的坐标为（4，3），C点的坐标为（0，3），
设过点D的反比例函数的解析式为y＝kx，代入D点坐标得k＝12，
∴y＝12x，
∵D是BC的中点，
∴点E的横坐标为8，
∵点E也在反比例函数图象上，
∴E点的坐标为（8，32），
设DE所在直线的函数解析式为y＝kx+b，代入D、E两点坐标得3=4k+b32=8k+b，
解得k=-38b=92，
∴y＝﹣38x+92；
（2）∵直线DE与x轴和y轴的交点分别为M、N，
∴M（12，0），N（0，92）
∴NC＝92﹣3＝32，OM＝12，
∴△CMN的面积＝12×32×12＝9．
29．解：(1)过点A作AD⊥y轴于点D，如图，

∵C(0,8)，A(3，a)，∴AD=3，OC=8.
∴S△AOC＝×OC×AD=×8×3＝12；
(2)∵A(3，a)，B(1，b)两点在反比例函数 (x＞0)的图象上，
∴3a＝b.
∵＝4，
∴|a－b|＝4.
∵由图象可知a＜b，
∴a－b＝－4.
∴，解得
∴A(3,2)，B(1,6) .
把A点的坐标代入(x＞0)得，，
∴k＝6.
∴反比例函数的解析式为 (x＞0)；
设一次函数的解析式为y＝mx＋n，
∵一次函数的图象经过点A，B，
∴.
解得.
∴一次函数的解析式为y＝－2x＋8.
30．解：（1）∵二次函数的对称轴为，
∴﹣=﹣，
解得a=2，
∵二次函数y=ax2+2x+c（a＞0）图象的顶点M在反比例函数上，
∴顶点为（﹣，c﹣），
∴（c﹣）=﹣3，
解得c=﹣，
∴二次函数的解析式为y=2x2+2x﹣；
（2）∵二次函数的解析式为y=2x2+2x﹣；
∴令y=0，2x2+2x﹣=0；
解得x=．
∴AB==2；
（3）根据对称轴x=﹣，当x=﹣时，y=﹣3a，
∴NO+MN=+3a≥2=2，当3a=时NO+MN最小，
即3a2=1时，a=，
∴此时二次函数的解析式为y=x2+2x+3．