





第8讲 一元一次不等式(组)及其应用-2021年中考数学一轮复习知识考点习题课件(19张)
展开1.(2020·杭州)若a>b,则( )
A.a-1≥b B.b+1≥a C.a+1>b-1 D.a-1>b+1
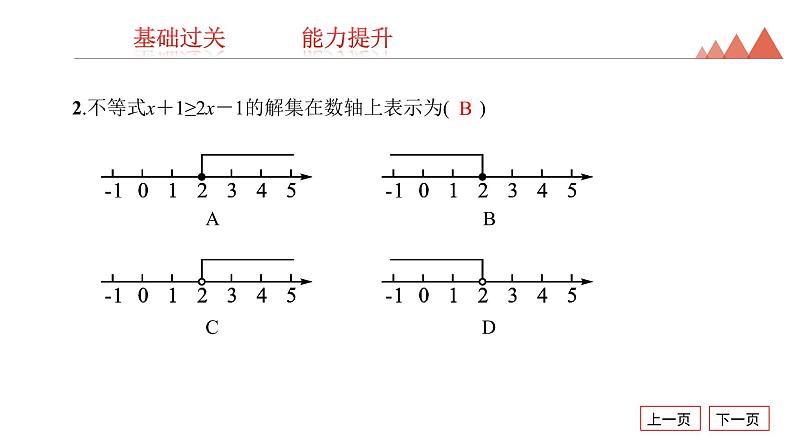
2.不等式x+1≥2x-1的解集在数轴上表示为( )
A B C D
3.(2020·广东)不等式组 的解集为( )
A.无解 B.x≤1 C.x≥-1 D.-1≤x≤1
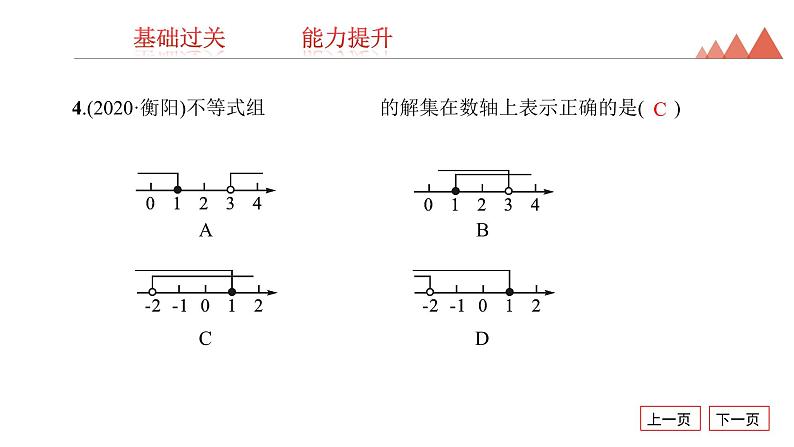
4.(2020·衡阳)不等式组 的解集在数轴上表示正确的是( )
5.(2020·德州)若关于x的不等式组 的解集是x<2,则a的取值范围是( )
A.a≥2 B.a<-2 C.a>2 D.a≤2
6.(2020·河南)已知关于x的不等式组 其中a,b在数轴上的对应点如图所示,则这个不等式组的解集为______________.
7.(2020·攀枝花)世纪公园的门票是每人5元,一次性购门票满40张,每张门票可少1元.若少于40人时,一个团队至少要有_________人进公园,买40张门票反而划算.
8.(2020·宁夏)《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某兴趣小组阅读四大名著的人数同时满足以下三个条件:
(1)阅读过《西游记》的人数多于阅读过《水浒传》的人数;(2)阅读过《水浒传》的人数多于阅读过《三国演义》的人数;(3)阅读过《三国演义》的人数的2倍多于阅读过《西游记》的人数. 若阅读过《三国演义》的人数为4,则阅读过《水浒传》的人数的最大值为______.
9.(2020·淮安)解不等式:
解:去分母,得2(2x-1)>3x-1.……(1)请完成上述解不等式的余下步骤;
解:去括号,得4x-2>3x-1.移项,得4x-3x>2-1.合并同类项,得x>1.
(2)解题回顾:本题“去分母”这一步的变形依据是______.(填“A”或“B”)
A.不等式两边都乘(或除以)同一个正数,不等号的方向不变B.不等式两边都乘(或除以)同一个负数,不等号的方向改变
10.(2020·枣庄)解不等式组 并求它的所有整数解的和.
11.仙桃是遂宁市某地的特色时令水果,仙桃一上市,水果店的老板用2 400元购进一批仙桃,很快售完;老板又用3 700元购进第二批仙桃,所购件数是第一批的 倍,但进价比第一批每件多了5元.
(1)第一批仙桃每件进价是多少元?
(2)老板以每件225元的价格销售第二批仙桃,售出80%后,为了尽快售完,剩下的决定打折促销.要使得第二批仙桃的销售利润不少于440元,剩余的仙桃每件售价至多打几折?(利润=售价-进价)
12.(2020·龙东)若关于x的一元一次不等式组 有2个整数解,则a的取值范围是_______________.
13.若x为实数,则[x]表示不大于x的最大整数,例如:[1.6]=1,[π]=3,[-2.82]=-3等.[x]+1是大于x的最小整数,对任意的实数x都满足不等式组[x]≤x<[x]+1.利用这个不等式组,求出满足[x]=2x-1的所有解,其所有解为____________________.
x1=0.5,x2=1
14.(2019·凉山)根据有理数乘法(除法)法则可知:
① 若 则 或②若 则 或下面求不等式(x-2)(x+3)>0的解集.
解:原不等式可化为① 或② 解不等式组①,得x>2.解不等式组②,得x<-3,∴原不等式的解集为x<-3或x>2.
请你运用所学知识,结合上述材料解答下列问题:(1)不等式x2-2x-3<0的解集为_____________;(2)不等式 的解集为________________________.
15.某市教育局对某镇实施“教育精准扶贫”,为该镇建立了中、小型两种图书馆.若建立3个中型图书馆和5个小型图书馆需要30万元,建立2个中型图书馆和3个小型图书馆需要19万元.
(1)建立一个中型图书馆和一个小型图书馆各需要多少万元?
2024中考数学一轮复习讲练测(全国通用)第08讲一元一次不等式(组)及其应用(课件): 这是一份2024中考数学一轮复习讲练测(全国通用)第08讲一元一次不等式(组)及其应用(课件),共50页。PPT课件主要包含了知识建构,考点精讲,考情分析,第一部分,第二部分,第三部分,不等式的性质,x≥5等内容,欢迎下载使用。
2024贵州中考数学一轮知识点复习 第8讲 分式方程及其应用(课件): 这是一份2024贵州中考数学一轮知识点复习 第8讲 分式方程及其应用(课件),共34页。PPT课件主要包含了分式方程及其应用,考点精讲,整式方程,――→,x=a,实际应用,一般步骤,常考类型及等量关系,分式方程及其实际应用,x-2等内容,欢迎下载使用。
2024贵州中考数学一轮知识点复习 第6讲 一次方程(组)及其应用(课件): 这是一份2024贵州中考数学一轮知识点复习 第6讲 一次方程(组)及其应用(课件),共31页。PPT课件主要包含了考点精讲,等式的性质,b±c,一元一次方程及其解法,解法步骤与注意事项,-2x-2=6x,二元一次方程组的解法,加减消元法,行程问题,追及问题等内容,欢迎下载使用。












