初中数学青岛版八年级下册10.6 一次函数的应用多媒体教学课件ppt

这是一份初中数学青岛版八年级下册10.6 一次函数的应用多媒体教学课件ppt，共30页。PPT课件主要包含了温故知新，练一练，热热身，试试身手，考考你，作业布置，课下拓展延伸等内容，欢迎下载使用。

1.一次函数图象的画法.
通常过 ， 两点画一条 ，就是函数y=kx+b（k≠0）的图象.
先设出表达式中的 ，再根据所给条件，利用 确定这些未知数.这种方法叫待定法.
3.一次函数的图象与性质.
图象：一次函数y=kx+b（k≠0）的图象是一条 ，通常叫做直线y=kx+b.
性质：对于一次函数y=kx+b，当 时，y随x的 而 ；当 时，y随x的 而 .
y x
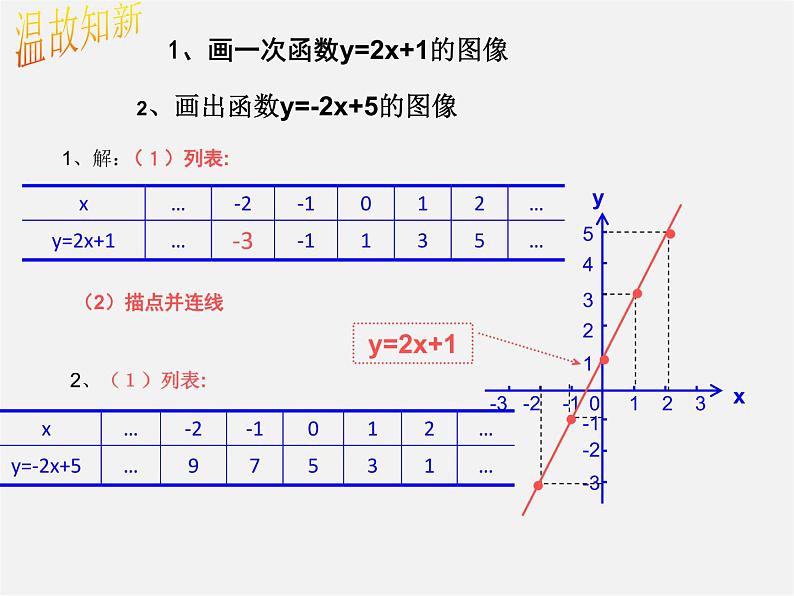
1、画一次函数y=2x+1的图像
2、画出函数y=-2x+5的图像
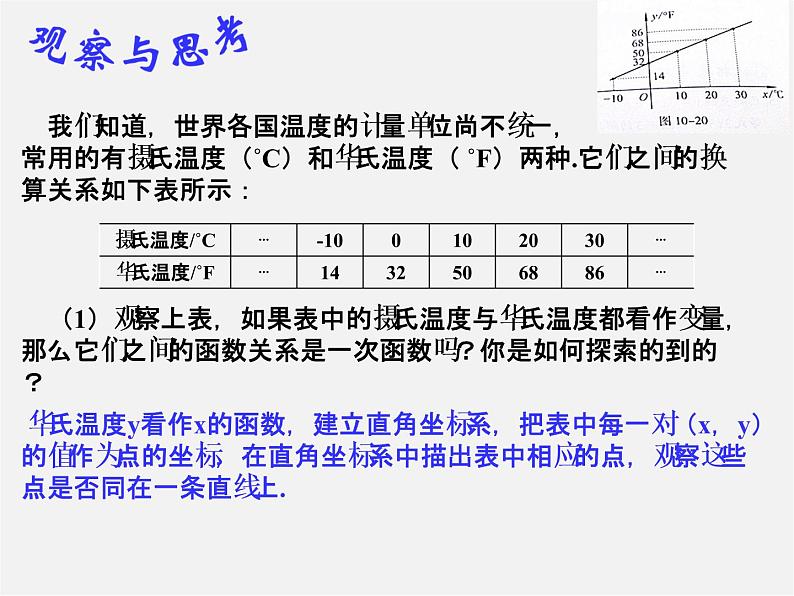
我们知道，世界各国温度的计量单位尚不统一，常用的有摄氏温度（˚C）和华氏温度（ ˚F）两种.它们之间的换算关系如下表所示：
（1）观察上表，如果表中的摄氏温度与华氏温度都看作变量，那么它们之间的函数关系是一次函数吗？你是如何探索的到的？
华氏温度y看作x的函数，建立直角坐标系，把表中每一对（x，y）的值作为点的坐标，在直角坐标系中描出表中相应的点，观察这些点是否同在一条直线上.
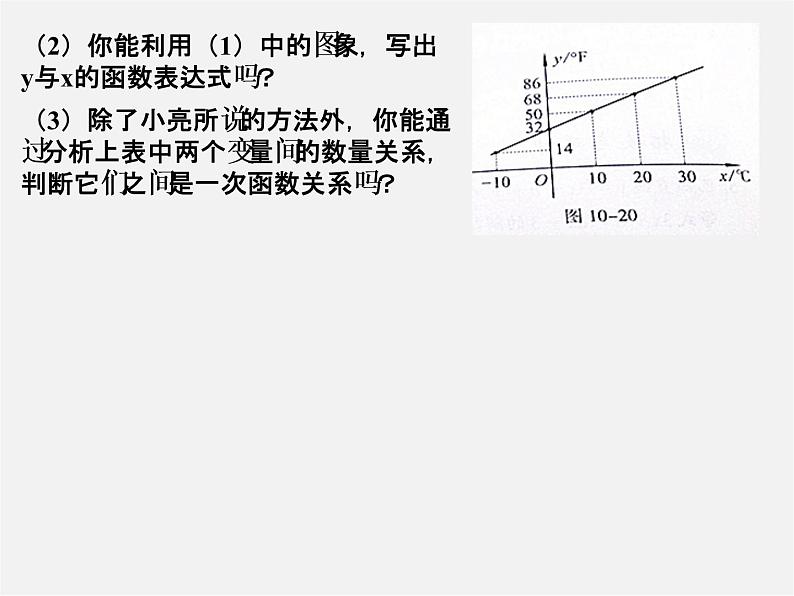
（2）你能利用（1）中的图象，写出y与x的函数表达式吗？
（3）除了小亮所说的方法外，你能通过分析上表中两个变量间的数量关系，判断它们之间是一次函数关系吗？
（4）你能求出华氏温度为0度（即0˚F ）时，摄氏温度是多少度？
当y=0时，0=1.8x+32，解得x= ，所以华氏温度为0 ˚F 时，摄氏温度是 ˚C.
（5）华氏温度的值与对应的摄氏温度的值有相等的可能吗？你会用哪几种方法解决这个问题？与同学交流.
有可能相等.当两值相等时 ，解得 .即当华氏温度为-40˚F时，摄氏温度为-40˚C ，温度值相等.
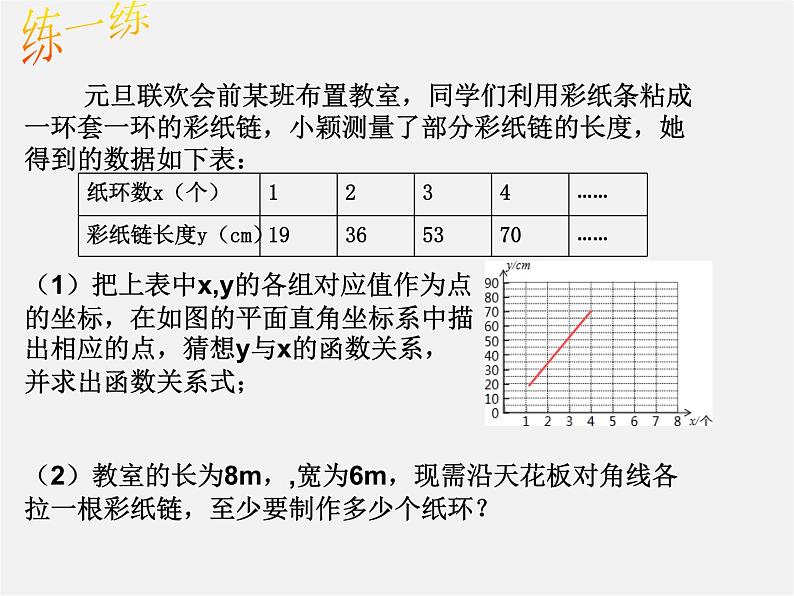
　　　元旦联欢会前某班布置教室，同学们利用彩纸条粘成一环套一环的彩纸链，小颖测量了部分彩纸链的长度，她得到的数据如下表：（1）把上表中x,y的各组对应值作为点的坐标，在如图的平面直角坐标系中描出相应的点，猜想y与x的函数关系，并求出函数关系式；（2）教室的长为8m，,宽为6m，现需沿天花板对角线各拉一根彩纸链，至少要制作多少个纸环？
为了迎接新学年的到来，时代中学计划开学前购买篮球和排球共20个，已知篮球每个80元，排球每个60元，设购买篮球x个，购买篮球和排球的总费用为y元.
（1）求y与x的函数表达式；
（2）如果要求篮球的个数不少于排球个数的3倍，应如何购买才能使总费用最少？最少费用是多少元？
山青林场计划购买甲、乙两种树苗共800株，甲种树苗每株24元，一种树苗每株30元.根据相关资料，甲、乙两种树苗的成活率分别是85%，90%.
（1）如果购买这两种树苗共用去21000元，甲、乙两种树苗各买了多少株？
（2）如果为了保证这批树苗的总成活率不低于88%，甲种树苗至多购买多少注？
（3）在（2）的条件下，应如何选购树苗，使购买树苗的费用最低？并求最低费用.
（1）设购买甲种树苗x株，乙种树苗y株，根据题意，得
经检验，方程组的解符合题意.所以购买甲种树苗500株，乙种树苗300株.
（2）设购买甲种树苗z株，乙种树苗（800-z）株，由题意得
0.85z+0.9×（800-z）≥0.88×800，
所以甲种树苗至多购买320株.
（3）设购买甲种树苗t株，购买树苗的费用为w元，由题意得
w=24t+30×（800-t）==-6t+24000，
所以w是t的一次函数，且由于k=-6<0，因此w随t增大而减小.由（2）知t≤320，因此，当t最大即t=320时，w最小.这是800-320=480，w=-6×320+24000=22080.
所以购买甲种树苗320株、乙种树苗480株，费用最低，最低费用为22080元.
某车间共有工人20名，已知每名工人每天可制造甲种零件6个或乙种零件5个，且每制造一个甲种零件可获利润150元，每制造一个乙种零件可获利润260元，车间每天安排x名工人制造甲种零件，其余工人制造乙种零件．（1）请写出此车间每天所获利润y（元）与x（名）之间的函数关系式；（2）若要使车间每天所获利润不低于24000元，你认为至少要派多少名工人去制造乙种零件才合适？
在例1 的解决过程中，是从现实生活中抽象出数学问题，用数学符号建立函数表达式，表示数学问题中变量之间的数量关系和变化规律.因此函数也是一种重要的数学模型.
1、取若干个形如图中的小梯形，按下图的方式排列，随着小梯形个数的增加，所拼得的四边形的周长也不断增加。
（2）你能探索L与n之间的函数解析式吗？这个函数是一次函数吗？试写出L与n的函数解析式。
（3）求n=20时L的值。
北京某厂和上海某厂同时制成电子计算机若干台，北京厂可支援外地10台，上海厂可支援外地4台，现在决定给重庆8台，汉口6台。假定每台计算机的运费如下表,求
（1）若总运费为8400元，上海运往汉口应是多少台？
（2）若要求总运费不超过8200元，共有几种调运方案？
（3）求出总运费最低的调运方案，最低总运费是多少元？
课本157页 习题10.6第2、3题
1、 如下图，L1反映了某公司产品的销售收入与销售量的 关系，L2反映该公司产品的销售成本与销售量的关系。
问1：这个图象与前一 节课所看到的图 象有何不同？
问2：你能说出这两 个函数代表的函数 的自变量与因变量分别指什么？
问3：你能说出x轴、y 轴分别表示什么量？
2、 如下图，L1反映了某公司产品的销售收入与销售量的 关系，L2反映该公司产品的销售成本与销售量的关系。
根据图象回答：1）当销售为2吨时，销售收入是 元。销售成本是 元。
2）当销售为6吨时，销售收入是 元。销售成本是 元。该公司赢利 元。
根据图象回答：3）当销售量为 时，销售收入等于销售成本。
4）当销售量 时， 该公司赢利。 （即收入大于成本）。当销售量 时， 该公司亏损 （即收入小于成本）。
3、如下图，L1反映了某公司产品的销售收入与销售量的 关系，L2反映该公司产品的销售成本与销售量的关系。
4、如下图，L1反映了某公司产品的销售收入与销售量的 关系，L2反映该公司产品的销售成本与销售量的关系。
5）L1对应的函数表达 式为 。 L2对应的函数表达 式是 。
5、如下图，L1反映了某公司产品的销售收入与销售量的 关系，L2反映该公司产品的销售成本与销售量的关系。
做了本题后你有什么体会或收获？（交流）
1、当同一直角坐标系中出 现多个函数图象时，一定 要注意对应的关系。2、根据函数的的图象的确定该函数的类型.
6、我边防局接到情报，近海处有一可疑船只A正向公海方向行使。边防局迅速派出快艇B追赶（如图（1）），图（2）中L1、L2分别表示两船相对海岸的距离S（海里）与追赶时间t（分）之间的关系。
我边防局接到情报，近海处有一可疑船只A正向公海方向行使。边防局迅速派出快艇B追赶（如图（1）），图（2）中L1，L2分别表示两船相对海岸的距离S（海里）与追赶时间t（分）之间的关系。
根据图象回答下列问题：1）哪条线表示B到海岸的距离与 追赶时间之间的关系？
2）A、B哪个速度快？3）15分钟内B能否追上A？
4）如果一直追上去，那么B能否 追上A？
5）当A逃到离海岸12海里的公海 时，B将无法对其进行检查。 照此速度，B能否在A逃入公 海前将其拦截？
根据图象回答下列问题：1）哪条线表示B到海岸的距离 与追赶时间之间的关系？ （交流）
2）A、B哪个速度快？
根据图象回答下列问题：1）哪条线表示B到海岸的距离与 追赶时间之间的关系？（交流）
3）15分钟内B能 否追上A？
2）A、B哪个速度快？ 3）15分钟内B能否追上A？
4）如果一直 追上去，那 么B能否追上 A？
4）如果一直追上去，那么B能否追上A？
5）当A逃到离海岸12海里 的公海时，B将 无法对其进行检 查。照此速度， B能否在A逃入 公海前将其拦截？
5）当A逃到离海岸12海里的公海时，B将无法对其进行检查。照此速度，B能否在A逃入公海前将其拦截？
7、你能求出两直线的表达式吗?