青岛版九年级上册3.3 圆周角备课ppt课件

这是一份青岛版九年级上册3.3 圆周角备课ppt课件，共13页。PPT课件主要包含了回顾旧知，观察与思考，定理的应用，课堂小结，当堂达标等内容，欢迎下载使用。

圆周角定理：圆周角等于它所对弧上的圆心角的一半．
推论１ ：圆周角的度数等于它所对弧的度数的一半．
推论２ ：同弧或等弧所对的圆周角相等；在同圆或等圆中，相等的圆周角所对的弧相等．
推论3 ：直径所对的圆周角是直角；９０°的圆周角所对的弦是直径．
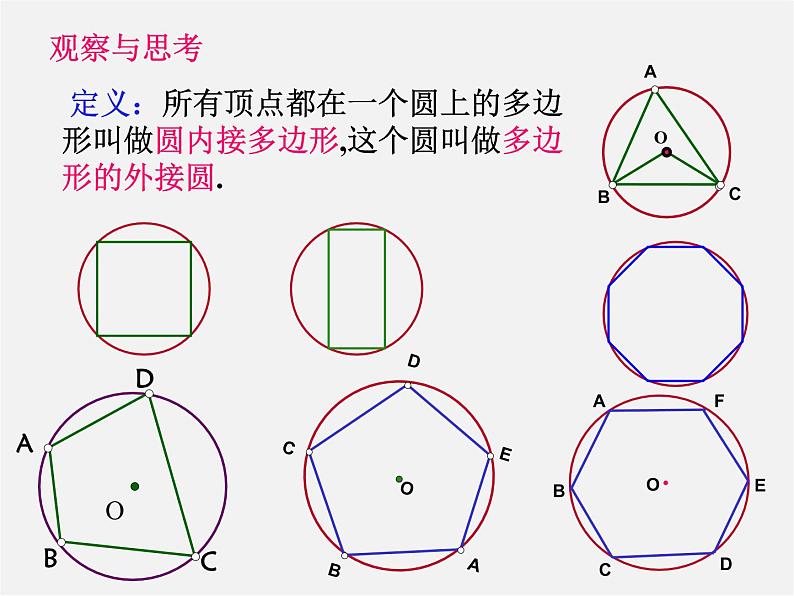
定义：所有顶点都在一个圆上的多边形叫做圆内接多边形,这个圆叫做多边形的外接圆.
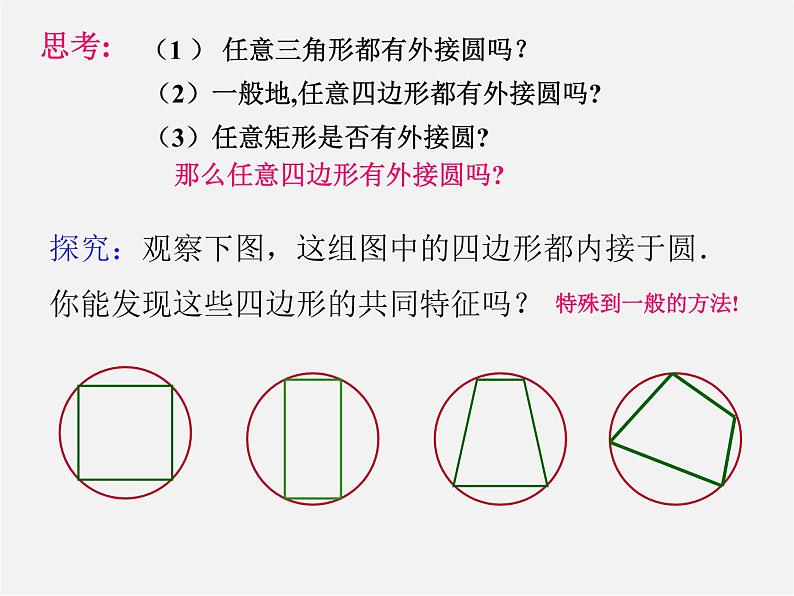
探究：观察下图，这组图中的四边形都内接于圆．你能发现这些四边形的共同特征吗？
（1 ） 任意三角形都有外接圆吗？
那么任意四边形有外接圆吗?
（3）任意矩形是否有外接圆?
（2）一般地,任意四边形都有外接圆吗?
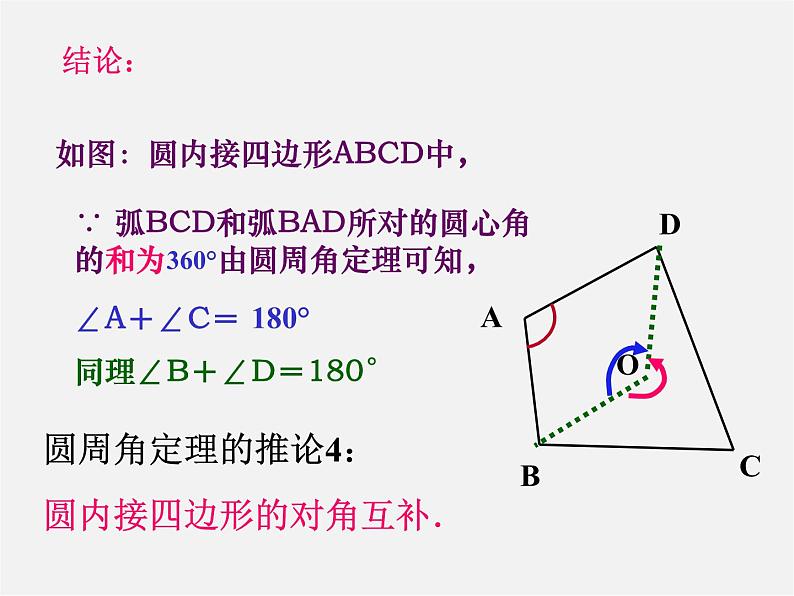
如图：圆内接四边形ABCD中，
∵ 弧BCD和弧BAD所对的圆心角的和为360°由圆周角定理可知，
∠A＋∠C＝ 180°
同理∠B＋∠D＝180°
圆周角定理的推论4：圆内接四边形的对角互补．
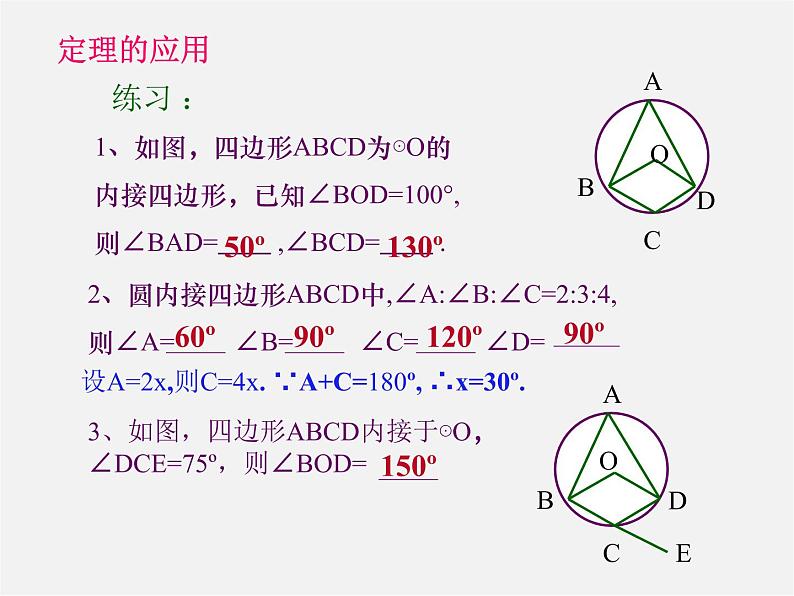
1、如图，四边形ABCD为⊙O的内接四边形，已知∠BOD=100°,则∠BAD= ,∠BCD= .
2、圆内接四边形ABCD中,∠A:∠B:∠C=2:3:4,则∠A= ∠B= ∠C= ∠D=
3、如图，四边形ABCD内接于⊙O， ∠DCE=75º，则∠BOD=
设A=2x,则C=4x. ∵A+C=180º, ∴x=30º.
例4：如图3-33，四边形ABCD内接于⊙O， 已知∠BOD=140°，求∠C的度数。
例5：如图3--34，△ABC内接于⊙O，D，F分别是弧AC与弧AB上的点，且弧BF=弧DA。连接AF并延长交CB的延长线与点E,连接AD，CD 求证：∠CAD=∠E
1:四边形ABCD内接于⊙O，则∠A+∠C=__ ，∠B+∠ADC=_____;若∠B=800， 则∠ADC=______ ∠CDE=______(图5) 2:四边形ABCD内接于⊙O，∠AOC=1000 则∠B=______∠D=______(图6) 3:四边形ABCD内接于⊙O, ∠A:∠C=1:3,则∠A=_____,
4:若ABCD为圆内接四边形，则下列哪个选项可能成立（ ）（A）∠A∶∠B∶∠C∶∠D ＝ 1∶2∶3∶4（ B）∠A∶∠B∶∠C∶∠D ＝ 2∶1∶3∶4（ C）∠A∶∠B∶∠C∶∠D ＝ 3∶2∶1∶4（D）∠A∶∠B∶∠C∶∠D ＝ 4∶3∶2∶1