初中青岛版2.5 解直角三角形的应用授课ppt课件

这是一份初中青岛版2.5 解直角三角形的应用授课ppt课件，共12页。PPT课件主要包含了方位角，射线OA，射线OE，射线OF，射线OG，射线OH，认识方位角，北偏西70°，南偏东60°，射线OB等内容，欢迎下载使用。

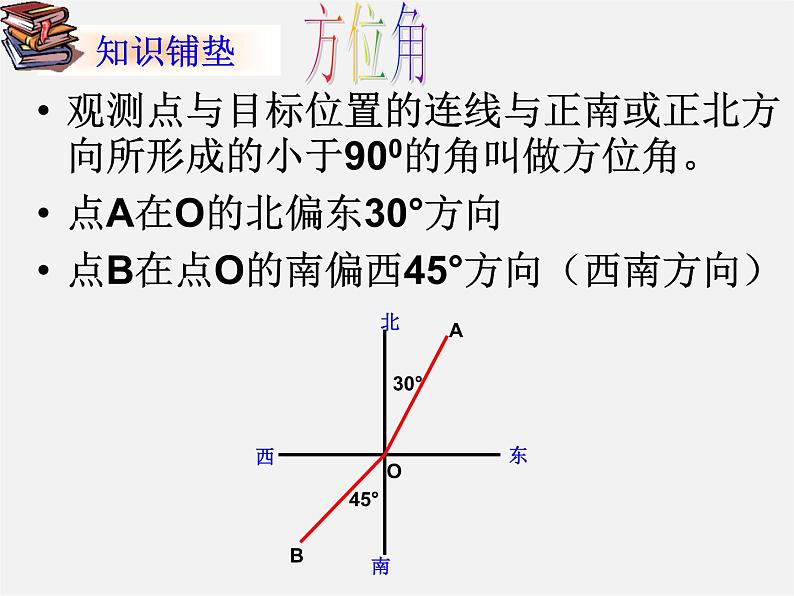
观测点与目标位置的连线与正南或正北方向所形成的小于900的角叫做方位角。点A在O的北偏东30°方向点B在点O的南偏西45°方向（西南方向）
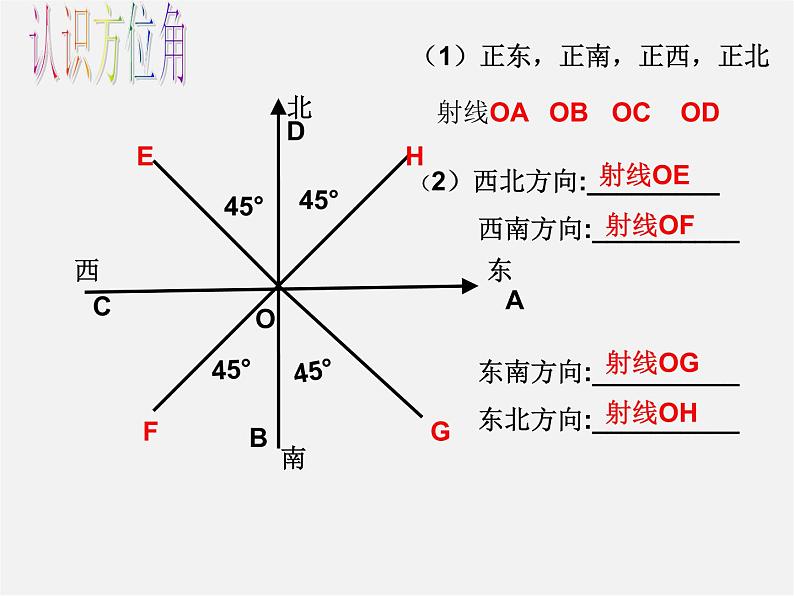
（1）正东，正南，正西，正北
（2）西北方向:_________ 西南方向:__________ 东南方向:__________ 东北方向:__________
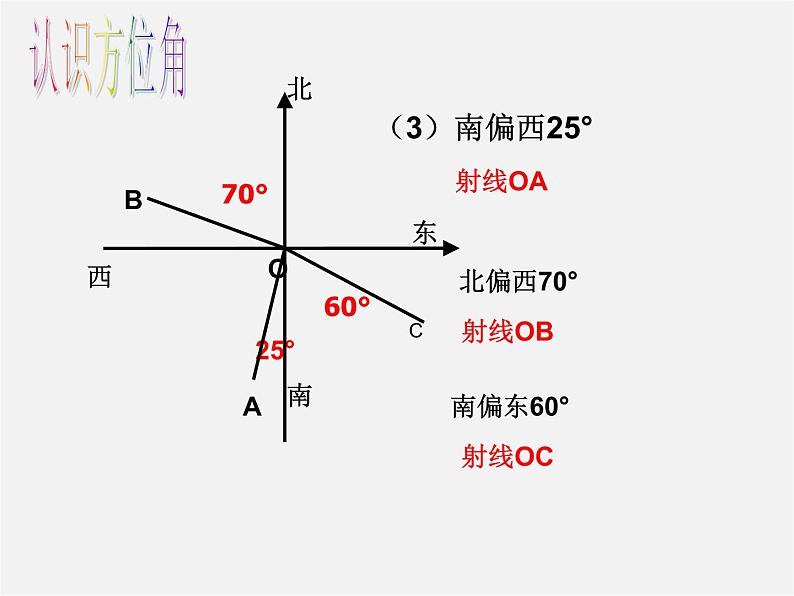
（3）南偏西25°
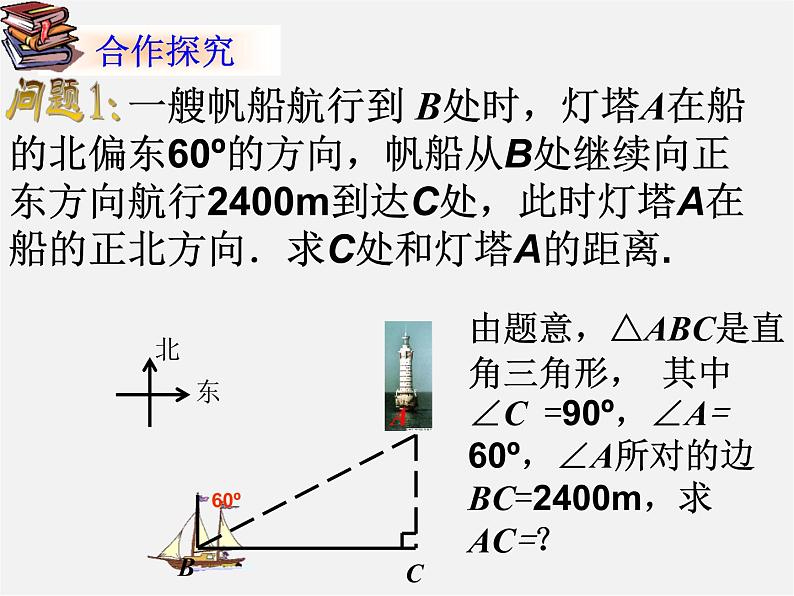
一艘帆船航行到 B处时，灯塔A在船的北偏东60º的方向，帆船从B处继续向正东方向航行2400m到达C处，此时灯塔A在船的正北方向．求C处和灯塔A的距离.
A
由题意，△ABC是直角三角形， 其中∠C =90º，∠A= 60º，∠A所对的边BC=2400m，求 AC=？
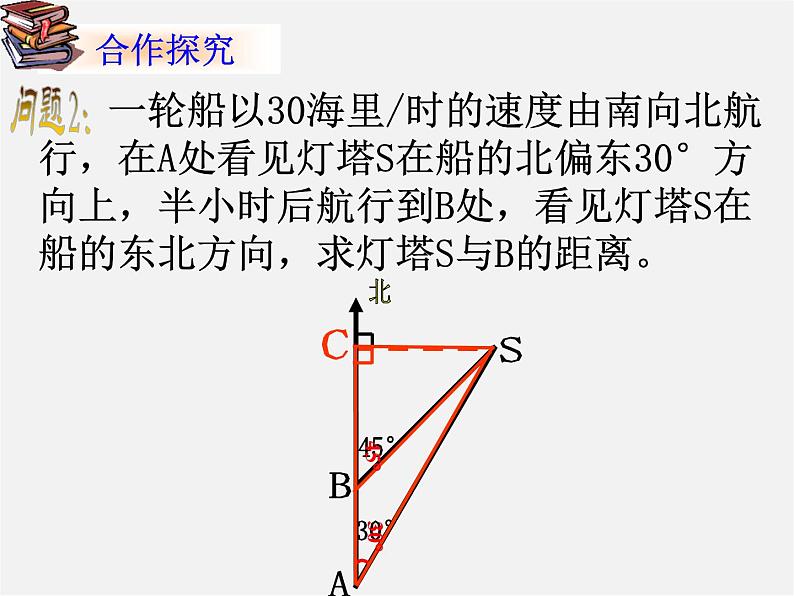
一轮船以30海里/时的速度由南向北航行，在A处看见灯塔S在船的北偏东30°方向上，半小时后航行到B处，看见灯塔S在船的东北方向，求灯塔S与B的距离。
如下图所示，一渔船上的渔民在A处看见灯塔M在北偏东60°方向，这艘渔船以28海里/时的速度向正东航行，半小时至B处，在B处看见灯塔M在北偏东15°方向，此时灯塔M与渔船的距离是多少海里？
方法：可添加适当的辅助线，把一般三角形问题转化成解直角三角形问题.
3．转化（化归）思想.
1.如图，一艘海轮位于灯塔P的北偏东45°方向，距离灯塔80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东30°方向上的B处，这时，海轮所在的B处距离灯塔P有多远？
2.海中有一个小岛A，它的周围8海里范围内有暗礁，渔船跟踪鱼群由西向东航行，在B点测得小岛A在北偏东60°方向上，航行12海里到达D点，这时测得小岛A在北偏东30°方向上，如果渔船不改变航线继续向东航行，有没有触礁的危险？