30°，45°，60°角的三角比PPT课件免费下载

青岛版初中数学九年级上册课文《30°，45°，60°角的三角比》,完整版PPT课件免费下载，优秀PPT背景图搭配，精美的免费ppt模板。轻松备课，欢迎免费下载使用。

一、【新课导入】

在直角三角形中,若一个锐角确定,那么这个角的对边, 邻边和斜边之间的比值也随之确定.
sinA和csB,csA和sinB有什么关系?tanA和tanB呢？
sinA=csB, csA＝sinB ， tanA·tanB=1
.如图,河岸AD,BC互相平行,桥AB垂直于两岸.桥长AB=12m,在C处看桥两端A,B, 夹角∠BCA=600. 求B,C间的距离. (你是怎样做的?)
交流探索:若知道tan∠BCA （ 即tan60°） 的值,根据上述条件能否直接求出B,C间的距离?
300,450,600角的三角比
课 题:
二、【学习目标】

掌握300,450,600角的三角比的值， 能够利用300,450,600角的三角比的值熟练地进行运算能够根据300,450,600角的三角比的值求出角的度数利用300,450,600角的三角比的值解决实际问题掌握互为余角的三角比之间的关系
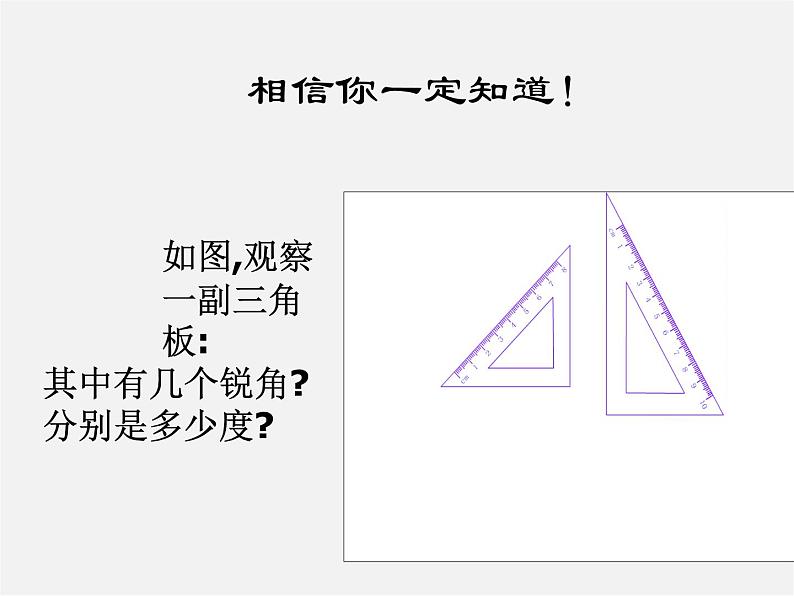
如图,观察一副三角板:其中有几个锐角?分别是多少度?

三、【课程的主要内容】

自学课本41页—43页实验与探究（1）、（2）、（3），完成后面的观察与思考，时间6分钟。有疑问的地方同桌之间讨论解决。
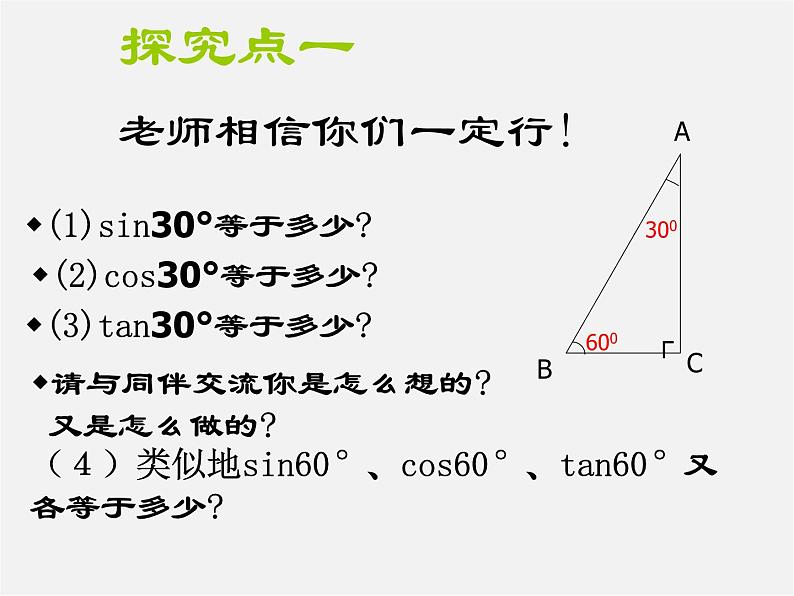
(1)sin30°等于多少?
(2)cs30°等于多少?
(3)tan30°等于多少?
请与同伴交流你是怎么想的? 又是怎么做的?
（４）类似地sin60°、cs60°、tan60°又 各等于多少?
（1）sin30°,cs30 °,tan30 °的值分别是多少？ △ABC是怎样的三角形？为什么？
因为∠A= ∠B=60 °， 所以△ABC 是等边三角形，且CD是AB边上的高，AD=BD.在Rt△ADC中，∠ADC=90°， ∠A=30°设AC=1，那么AD= AB= ，
cs30°=（ ）
tan30°=（ ）
（2）利用下图，你会求出60°的正弦、余弦、正切的值吗？
(5)sin45°等于多少?
cs45°等于多少?
tan45°等于多少?
（3）sin45°,cs45 °,tan45 °的值分别是多少？
在Rt△ABC中，∠C=90°， ∠A=45° ．设AC=1，那么BC=AC=1，所以
从填写的表格中，你发现了哪些规律？
sin 30° = cs 60°
sin 60° = cs 30°
tan 30°· tan 60°=1
sin 45° = cs 45°
如果∠A ＋ ∠B=90 ° ，那么sin A = csB , cs A = sinB ．tanA·tanB=1
自学课本43页例1，注意计算的正确性，时间3分钟
例1 计算:(1)sin300+cs450;(2) sin2600+cs2600-tan450.
老师提示:Sin2600表示(sin600)2,cs2600表示(cs600)2,其余类推.
(1)sin600-tan450; (2)cs600+tan600;
老师期望:只要勇敢地走向黑板来展示自己,就是英雄!
小组合作探究课本43页例2，并独立完成44页习题3题，时间3分钟

四、【例题剖析】

例１求下列各式的值：（1）sin30°·cs45°（2）tan45 °－cs60°.
当A,B都是锐角时,如果sinA=sinB或csA=csB或tanA=tanB,那么A=B
例2 如图:一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为600,且两边摆动的角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差.(结果保留根号).
老师提示:将实际问题数学化.
如图,河岸AD,BC互相平行,桥AB垂直于两岸.桥长AB=12m,在C处看桥两端A,B, 夹角∠BCA=600. 求B,C间的距离.
3.如图,在Rt△ABC中,∠C=90°, ∠A,∠B ,∠C的对边分别是a,b,c.求证:sin2A+cs2A=1
如图，作边长为1 的正方形ABCD ．延长边CB 到D ′ ，使B D ′＝ B D，连接D D ′ ．你能利用这个图形求出22 . 5°角的正切的值吗？试一试．
（1）sin30°－cs30°=________; （2） ·tan60 °=_____.
（1）sin30°＋cs60°; （2）tan30 °· tan60 °;（3） 2sin60°－ tan30 °;（4） sin45°· cs45°＋ tan45 °．
3、、在Rt△ABC中，∠C=90°, 已知AB=2，∠A=45°, 解这个直角三角形。（先画图，后计算）

五、【拓展学习】

3、在Rt△ABC中，∠C=90°, 已知AB=2，∠A=45°,求AC的值 。（先画图，后计算）4、某商场有一自动扶梯，其倾斜角为30°，高为7m，扶梯的长度是多少？5、海船以30海里/时的速度向正北方向航行，在A处看灯塔Q在海船的北偏东30°处，半小时后航行到B处，发现此时灯塔Q与海船的距离最短，求（1）从A处到B处的距离（2）灯塔Q到B处的距离。（画出图形后计算，用根号表示）
直角三角形中的边角关系
直角三角形两锐角的关系.
直角三角形边与角之间的关系.
特殊角30°,45°,60°角的三角比值.
互余两角之间的三角函数关系
必做题 ：P44 习题2.2 1,2,3选做题(任选一题)1、甲、乙两楼相距50米，从乙楼底望甲楼顶仰角为60°，从甲楼顶望乙楼顶俯角为30°，求两楼的高度，要求画出正确图形。2、某型号飞机的机翼形状如图所示，AB∥CD，根据数据计算AC、BD和CD的长度(精确到0.1米， ≈1.414， ≈1.732).