
初中数学3.4 直线与圆的位置关系课前预习ppt课件
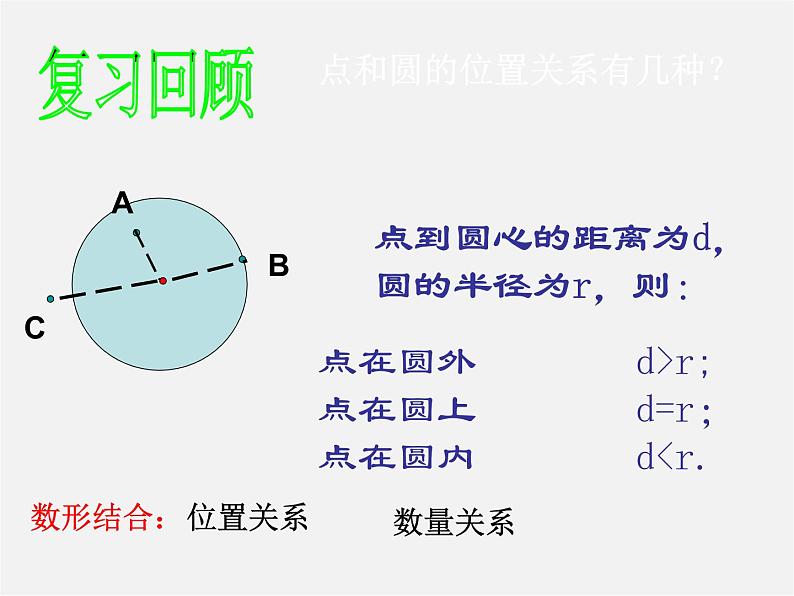
展开点和圆的位置关系有几种?
点到圆心的距离为d,圆的半径为r,则:
点在圆外 d>r;点在圆上 d=r;点在圆内 d
从海上日出这种自然现象中可以抽象出哪些基本的几何图形呢?
今天老师和同学们一起来探究
直线与圆的位置关系(一)
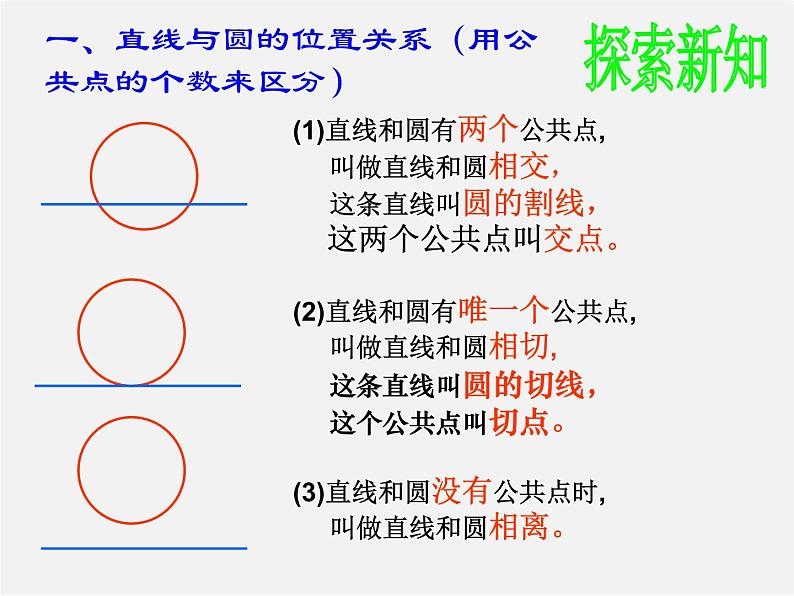
(2)直线和圆有唯一个公共点, 叫做直线和圆相切, 这条直线叫圆的切线, 这个公共点叫切点。
(1)直线和圆有两个公共点, 叫做直线和圆相交, 这条直线叫圆的割线, 这两个公共点叫交点。
(3)直线和圆没有公共点时, 叫做直线和圆相离。
一、直线与圆的位置关系(用公共点的个数来区分)
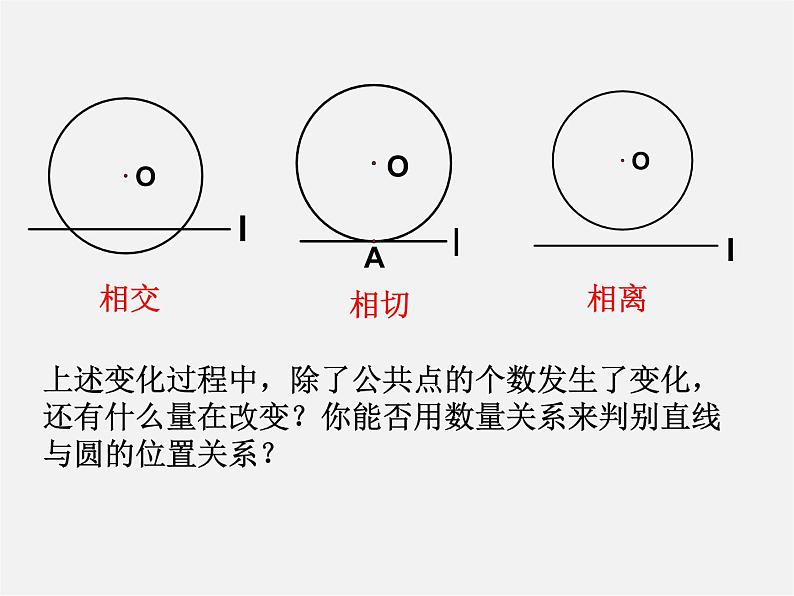
上述变化过程中,除了公共点的个数发生了变化,还有什么量在改变?你能否用数量关系来判别直线与圆的位置关系?
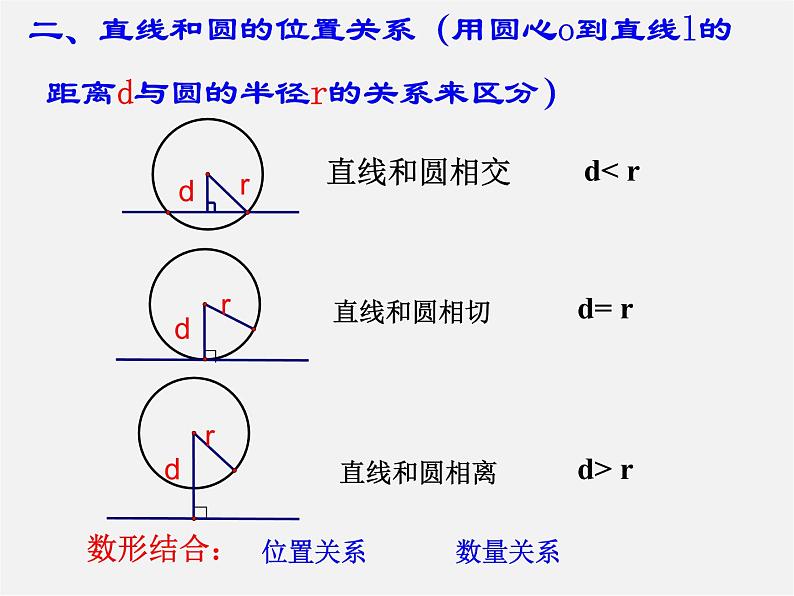
二、直线和圆的位置关系(用圆心到直线l的 距离d与圆的半径r的关系来区分)
判定直线 与圆的位置关系的方法有____种:
(1)根据定义,由________________ 的个数来判断;
(2)根据性质,由_________________ 的关系来判断。
在实际应用中,常采用第二种方法判定。
圆心到直线的距离d与半径r
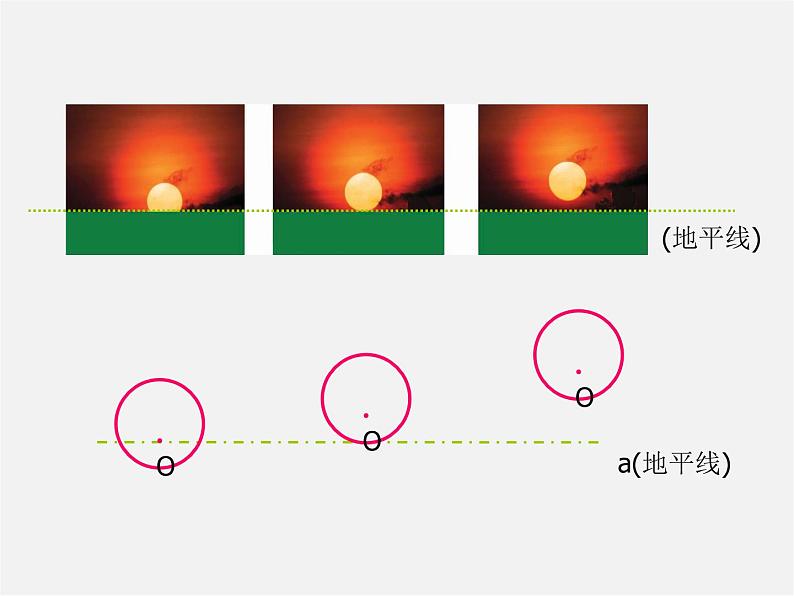
观察太阳落山的照片,在太阳落山的过程中,太阳与地平线(直线a)经历了哪些位置关系的变化?
4、直线L 和⊙O有公共点,则直线L与⊙O( ). A、相离;B、相切;C、相交;D、相切或相交。
例:在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?(1)r=2cm;(2)r=2.4cm (3)r=3cm.
分析:要了解AB与⊙C的位置关系,只要知道圆心C到AB的距离d与r的关系.已知r,只需求出C到AB的距离d。
解:过C作CD⊥AB,垂足为D
根据三角形的面积公式有
即圆心C到AB的距离d=2.4cm
所以 (1)当r=2cm时,
(2)当r=2.4cm时,
(3)当r=3cm时,
因此,⊙C和AB相交。
2、如图,已知∠BAC=30度,M为AC 上一点,且AM=5cm,以M为圆心、 r为半径的圆与直线AB有怎样的 位置关系?为什么?
(3) r=2.5cm
已知⊙A的直径为6,点A的坐标为(-3,-4),则x轴与⊙A的位置关系是_____, y轴与⊙A的位置关系是_____。
在Rt△ABC中,∠C=90°,AC=5cm,BC=12cm,以C为圆心,r为半径作圆。①当r满足 时, 直线AB与⊙C相离。②当r满足 时,直线AB与⊙C相切。③当r满足 时,直线AB与⊙C相交。
④当r满足 时, 线段AB与⊙C只有一个公共点。
3、如图,在Rt△ABC中,∠C=90°,AB=5cm,AC=3cm,以C为圆心的圆与AB相切,则这个圆的半径是 cm。
小结:1、直线与圆的位置关系:
2、判定直线 与圆的位置关系的方法有____种:
(1)根据定义,由__________________的个数来判断;
(2)根据性质,由_____________________ ______________的关系来判断。
练习:看谁做的又对又快
1、完成综训课本93页练习1、22、完成综训77页第一课时的1、2、4、5、6、7、8、9、10、11题.
数学青岛版3.4 直线与圆的位置关系图片ppt课件: 这是一份数学青岛版3.4 直线与圆的位置关系图片ppt课件,共60页。PPT课件主要包含了d=r,d>r,相切或相交,由此得到,这样就得到了,习题34,a>2或a<-2,a=±2,-2<a<2,解CD与⊙O相切等内容,欢迎下载使用。
数学九年级上册3.4 直线与圆的位置关系教学演示课件ppt: 这是一份数学九年级上册3.4 直线与圆的位置关系教学演示课件ppt,共13页。PPT课件主要包含了直线和圆相切,直线和圆相离,直线何时变为切线,切线的判定定理,切线判定定理的应用,探索切线性质,所以AB与CD垂直,切线的性质定理,切线的性质定理的应用,挑战自我等内容,欢迎下载使用。
初中数学青岛版九年级上册3.4 直线与圆的位置关系课文ppt课件: 这是一份初中数学青岛版九年级上册3.4 直线与圆的位置关系课文ppt课件,共26页。PPT课件主要包含了学习目标,预习检测,想一想,应用新知,回顾总结,课后延伸,祝你成功等内容,欢迎下载使用。













