初中数学青岛版九年级下册5.4二次函数的图像与性质集体备课课件ppt

这是一份初中数学青岛版九年级下册5.4二次函数的图像与性质集体备课课件ppt，共24页。PPT课件主要包含了学习目标，议一议，想一想，试一试，例题讲解，思维与拓展等内容，欢迎下载使用。

1.会用描点法画出二次函数y=ax2+k与y=a(x-h)2的图象；2.能结合图像确定抛物线y=ax2+k 与y=a(x-h)2 对称轴与顶点坐标
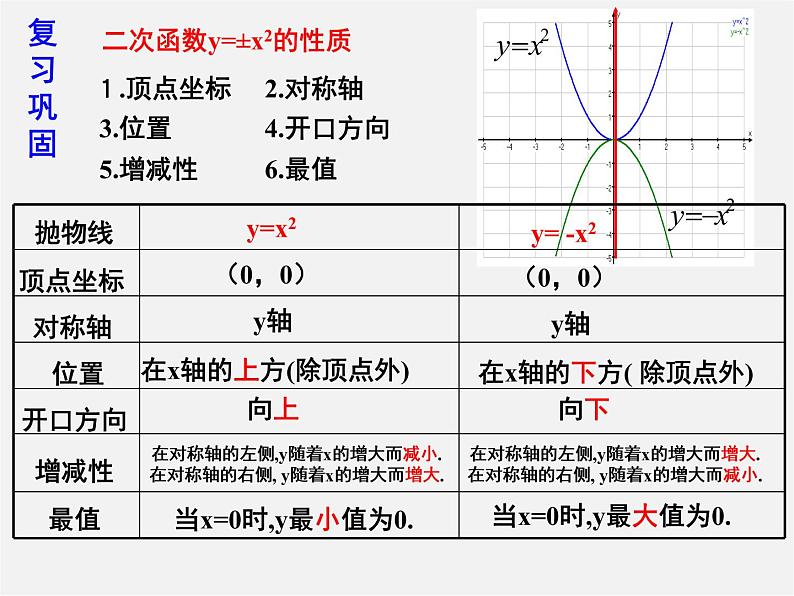
二次函数y=±x2的性质
１.顶点坐标 2.对称轴
3.位置 4.开口方向
5.增减性 6.最值
在x轴的上方(除顶点外)
在x轴的下方( 除顶点外)
当x=0时,y最小值为0.
当x=0时,y最大值为0.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
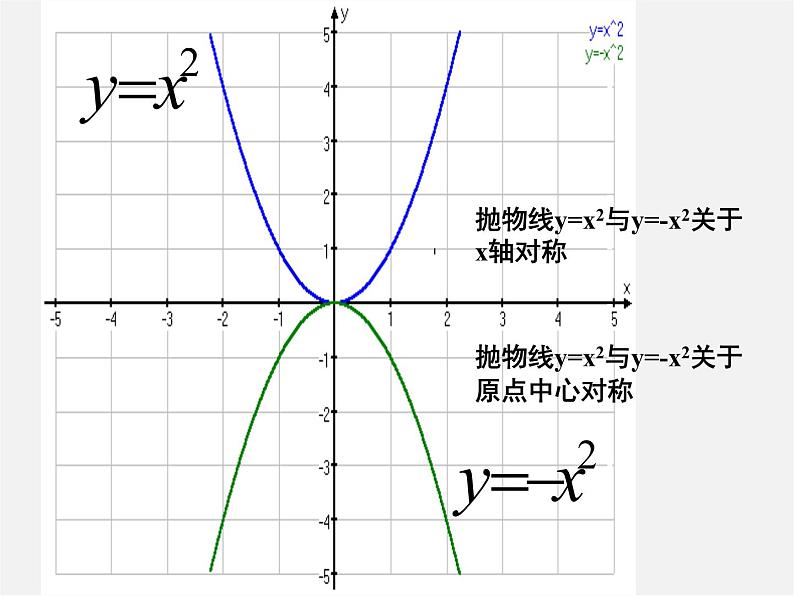
抛物线y=x2与y=-x2关于x轴对称
抛物线y=x2与y=-x2关于原点中心对称
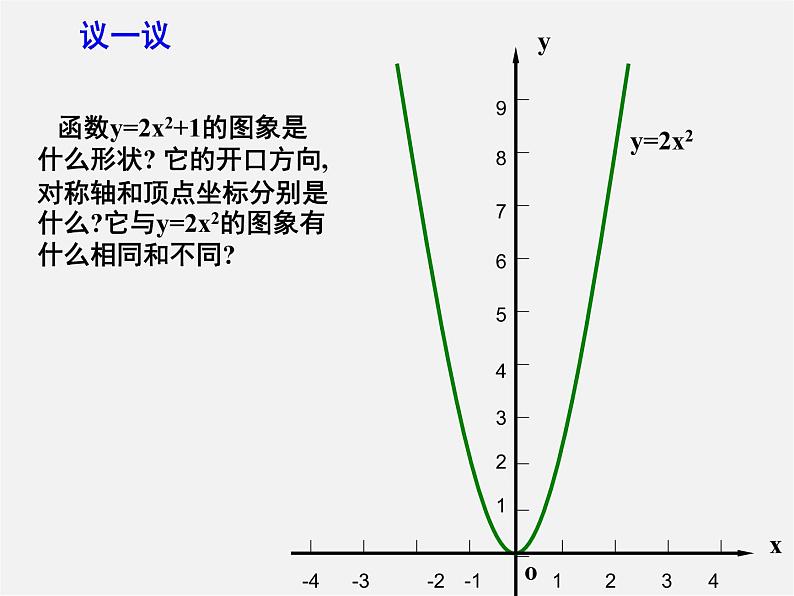
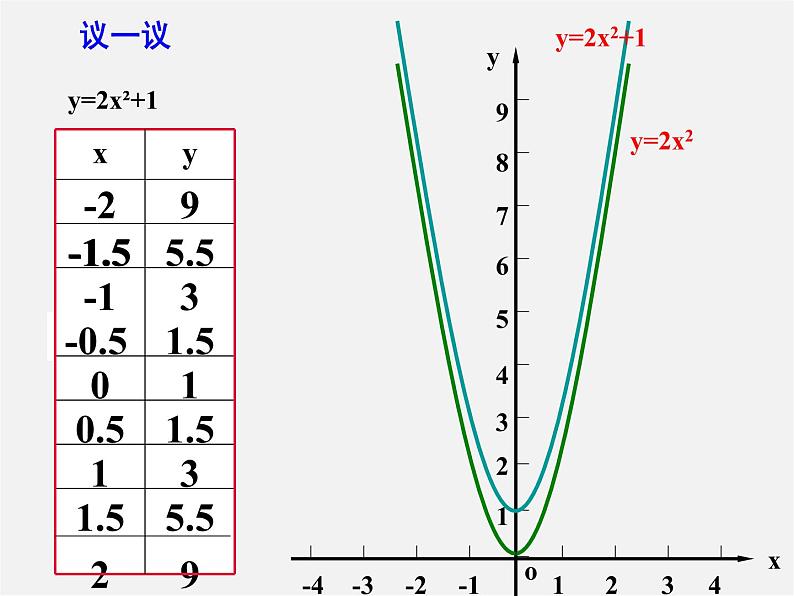
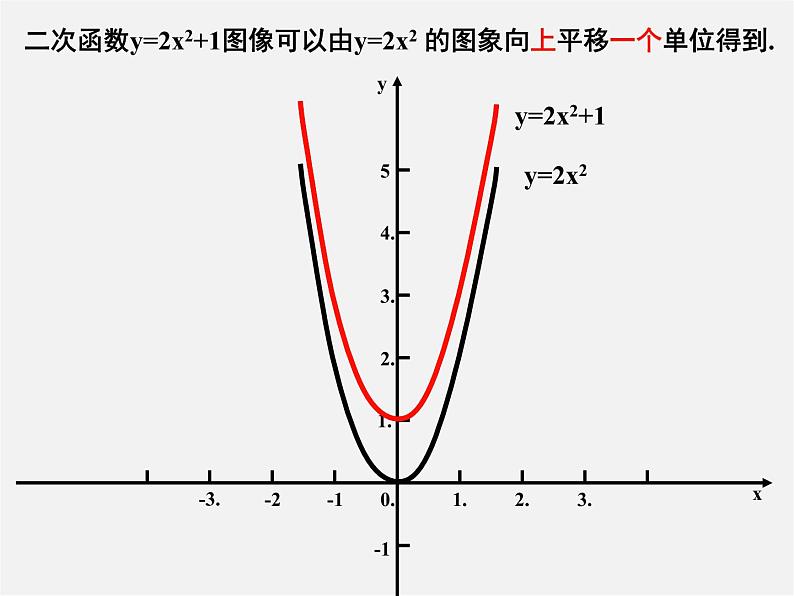
在同一坐标系中作出二次函数y=2x²+1的图象与二次函数y=2x²的图象.
二次函数y=2x²+1的图象与二次函数y=2x²的图象有什么关系?它们是轴对称图形吗?它的开口方向、对称轴和顶点坐标分别是什么?作图看一看．
函数y=2x2+1的图象是什么形状? 它的开口方向,对称轴和顶点坐标分别是什么?它与y=2x2的图象有什么相同和不同?
二次函数y=2x2+1图像可以由y=2x2 的图象向上平移一个单位得到.
二次项系数为2,开口向上;开口大小相同;对称轴都是y轴;增减性与也相同.
顶点不同,分别是原点(0,0)和(0,1).
二次函数y=2x2+1的图象是什么形状?它与二次函数y=2x2的图象有什么相同和不同?它的开口方向、对称轴和顶点坐标分别是什么?
位置不同;最小值不同:分别是1和0.
想一想,在同一坐标系中作二次函数y=-2x2+1和y=-2x2的图象,会是什么样?
二次函数y=2x2+1的图象形状与y=2x2一样,仍是抛物线.
二次项系数为-2,开口向下;开口大小相同;对称轴都是y轴;增减性与也相同.
二次函数y=-2x2+1的图象是什么形状?它与二次函数y=-2x2的图象有什么相同和不同?它的开口方向、对称轴和顶点坐标分别是什么?
位置不同;最大值不同:分别是1和0..
二次函数y=-2x2+1的图象形状与y=-2x2一样,仍是抛物线.
在同一坐标系中作出二次函数y=3x²-1的图象与二次函数y=3x²的图象.
二次函数y=3x²一l的图象与二次函数y=3x²的图象有什么关系?它们是轴对称图形吗?它的开口方向、对称轴和顶点坐标分别是什么?
你知道函数y=3x2-1的大致图象和位置吗?
二次函数y=3x2-1图像可以由y=3x2 的图象向下平移一个单位得到.
二次项系数为正数3,开口向上;开口大小相同;对称轴都是y轴;增减性与也相同.
顶点不同,分别是原点(0,0)和(0,-1).
二次函数y=3x2-1的图象是什么形状?它与二次函数y=3x2的图象有什么相同和不同?它的开口方向、对称轴和顶点坐标分别是什么?
位置不同;最小值不同:分别是-1和0.
想一想,在同一坐标系中作二次函数y=-3x2-1和y=-3x2的图象,会是什么样?
二次函数y=3x2-1的图象形状与y=3x2一样,仍是抛物线.
二次项系数为正数-3,开口向下;开口大小相同;对称轴都是y轴;增减性与也相同.
二次函数y=-3x2-1的图象是什么形状?它与二次函数y=-3x2的图象有什么相同和不同?它的开口方向、对称轴和顶点坐标分别是什么?
位置不同;最大值不同:分别是0和-1.
请你总结二次函数y=ax2+c的图象和性质.
二次函数y=-3x2-1的图象形状与y=-3x2一样,仍是抛物线.
y=ax2 +c(a>0)
y=ax2 +c(a<0)
当c>0时,在x轴的上方(经过一,二象限);当c<0时,与x轴相交(经过一,二三四象限).
当c<0时,在x轴的下方(经过三,四象限);当c>0时,与x轴相交(经过一,二三四象限).
当x=0时,最小值为c.
当x=0时,最大值为c.
根据图形填表：二次函数y=ax2+c的图象和性质.
由|a|来决定， |a|越大，开口越小， |a|越小，开口越大。
二次函数y=ax2与y=ax2+c的图象有什么关系？
二次函数y= ax2+c的图象可以由 y=ax2 的图象当c > 0 时 向上平移c个单位得到.当c < 0 时 向下平移-c个单位得到.
二次函数y= ax2+c的图象可以由 y=ax2 的图象上下平移|c|个单位得到。
1. y = -2x 2 +5 的图象可由抛物线 y = -2x 2 经过 得到的. 它的对称轴是 , 顶点坐标是 ,在x<0时.y值随x的增大而 ； 与x轴有 交点。
沿y轴向上平移5个单位
2.函数y=x2-1的图象，可由y=x2的图象向 ___ 平 移 　个单位.3.把函数y=3x2+2的图象沿x轴对折，得到的图 象的函数解析式为 .4.已知（m,n)在y=ax2+a的图象上，（- m,n ） _____（在，不在）y=ax2+a的图象上.5. 若y=x2+（2k-1）的顶点位于x轴上方，则 k_______
1. 一次函数y=ax+b与y=ax2-b在同一坐标系中的大致图象是（ ）
2. 函数y=ax2+a与y= （a≠0)在同一坐标系中的大致图象是（ ）
一：填空1.抛物线y=－3x2＋5的开口向________，对称轴是_______，顶点坐标是________，顶点是最_____点，所以函数有最________值是_____．2.抛物线y=4x2－1与y轴的交点坐标是_________，与x轴的交点坐标是_____．3.把抛物线y=x2向上平移3个单位后，得到的抛物线的函数关系式为_______．4.抛物线y=4x2－3是将抛物线y=4x2，向_____平移______个单位得到的．5.抛物线y=ax2－1的图像经过（4，－5），则a=________