初中数学5.7二次函数的应用教课内容课件ppt

这是一份初中数学5.7二次函数的应用教课内容课件ppt，共25页。PPT课件主要包含了0r45，∴抛物线的表达式为，我们来比较一下，-2-2，2-2，谁最合适，∴这时水面的宽度为，理解问题，检验结果的合理性，∵AB4等内容，欢迎下载使用。
1.会建立直角坐标系解决实际问题；2.会应用二次函数的性质解决实际问题.
（1）磁盘最内磁道的半径为r mm，其上每0.015mm的弧长为一个存储单元，这条磁道有多少个存储单元？（2）磁盘上各磁道之间的宽度必须不小于0.3mm，磁盘的外圆周不是磁道，这张磁盘最多有多少条磁道？（3）如果各磁道的存储单元数目与最内磁道相同，最内磁道的半径r是多少时，磁盘的存储量最大？
计算机把数据存储在磁盘上，磁盘是带有磁性物质的圆盘，磁盘上有一些同心圆轨道，叫做磁道，现有一张半径为45mm的磁盘，
你能说出r为多少时y最大吗？
分析（1）最内磁道的周长为2πr ㎜,它上面的存储单元的个数不超过
（2）由于磁盘上磁道之间的宽度必须不小于0.3㎜，磁盘的外圆周不是磁道，各磁道分布在磁盘上内径为r mm外径为 45 mm的圆环区域，所以这张磁盘最多有 条磁道.
(3)当各磁道的存储单元数目与最内磁道相同时，磁盘每面存储量=每条磁道的存储单元数x磁道数.设磁盘每面存储量为y,则
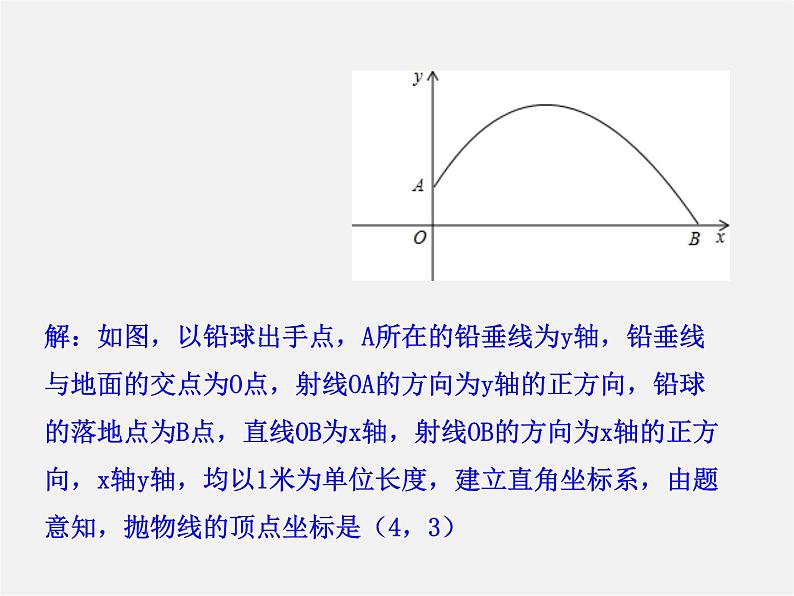
运动员掷一枚铅球，铅球抛出时离地面的高度为，抛出后，铅球行进的路线是一段抛物线，行进时距离地面的最大高度是3米，此时铅球沿水平方向行进了4米，求铅球从抛出到落地走过的水平距离.
解：如图，以铅球出手点，A所在的铅垂线为y轴，铅垂线与地面的交点为O点，射线OA的方向为y轴的正方向，铅球的落地点为B点，直线OB为x轴，射线OB的方向为x轴的正方向，x轴y轴，均以1米为单位长度，建立直角坐标系，由题意知，抛物线的顶点坐标是（4，3）
抛物线的表达式为y=a(x-4)2+3
x1=-2不合题意，x2=10符合题意
所以，铅球从抛出到落地走过的水平距离为10米.
图中是抛物线形拱桥，当水面在l时，拱顶离水面2 m，水面宽4 m，水面下降1 m时，水面宽度增加了多少？
解法一: 如图所示以抛物线的顶点为原点，以抛物线的对称轴为y轴，建立平面直角坐标系.
∴可设这条抛物线所表示的二次函数的解析式为:
当拱桥离水面2m时,水面宽4m
即抛物线过点(2,-2)
∴这条抛物线所表示的二次函数为:
当水面下降1 m时,水面的纵坐标为y=-3,这时有:
∴当水面下降1 m时,水面宽度增加了
解法二: 如图所示,以抛物线和水面的两个交点的连线为x轴，以抛物线的对称轴为y轴，建立平面直角坐标系.
此时,抛物线的顶点为(0,2)
当拱桥离水面2 m时,水面宽4 m
即:抛物线过点(2,0)
当水面下降1 m时,水面的纵坐标为y=-1,这时有:
解法三:如图所示,以抛物线和水面的两个交点的连线为x轴，以其中的一个交点(如左边的点)为原点，建立平面直角坐标系.
∵抛物线过点(0,0)
此时,抛物线的顶点为(2,2)
回顾解决问题的过程，你能总结一下解决此类问题的基本思路吗？与同伴交流.
2.分析问题中的变量和常量,以及它们之间的关系
3.用数学的方式表示出它们之间的关系;
“二次函数应用”的思路
1.如图，等腰Rt△ABC（∠ACB＝90º）的直角边与正方形DEFG的边长均为2，且AC与DE在同一直线上，开始时点C与点D重合，让△ABC沿这条直线向右平移，直到点A与点E重合为止．设CD的长为x，△ABC与正方形DEFG重合部分（图中阴影部分）的面积为y，则y与x之间的函数关系的图象大致是（ ）
2.如图所示,阳光中学教学楼前喷水池喷出的抛物线形水柱，其解析式为 ，则水柱的最大高度是（ ）Ａ.２ Ｂ.４ 　Ｃ.６　 Ｄ.２+3.已知二次函数　　　 的图象如图所示，有下列５个结论：①abc>0; ②b0;④2cm(am+b)(m为不等于1的实数).其中正确的结论有（ ）A.2个 B.3个 C.4个 D.5个
4.某工厂大门是一抛物线形的水泥建筑物,大门底部宽AB=4 m,顶部C离地面的高度为4.4 m,现有载满货物的汽车欲通过大门,货物顶部距地面2.7 m,装货宽度为2.4 m.这辆汽车能否顺利通过大门?若能,请你通过计算加以说明;若不能,请简要说明理由.
解析：如图，以AB所在的直线为x轴，以AB的垂直平分线为y轴，建立平面直角坐标系.
∴A(-2,0) B(2,0)
设抛物线所表示的二次函数为
∵抛物线过A(-2,0)
∴抛物线所表示的二次函数为
∴汽车能顺利经过大门.
5.某工厂在生产过程中要消耗大量电能，消耗每千度电产生利润与电价是一次函数关系，经过测算，工厂每千度电产生利润y(元/千度)与电价x(元/千度)的函数图象如图：（1）当电价为600元/千度时，工厂消耗每千度电产生利润是多少？（2）为了实现节能减排目标，有关部门规定，该厂电价x(元/千度)与每天用电量m(千度)的函数关系为x=10m+500，且该工厂每天用电量不超过60千度，为了获得最大利润，工厂每天应安排使用多少度电？工厂每天消耗电产生利润最大是多少元？
【解析】（1）工厂每千度电产生利润y(元/千度)与电价x(元/千度)的函数解析式为：y=kx+b.该函数图象过点（0，300），（500，200）∴ 500k+b=200 解得 k=- b=300 b= 300∴y=- x+300(x≥0)当电价x=600元/千度时，该工厂消耗每千度电产生利润y= 600+300=180（元/千度）（2）设工厂每天消耗电产生利润为w元，由题意得：W=my=m(- x+300)=m [- (10m+500)+300]化简配方，得：w=-2(m-50)2+5000由题意，m≤60, ∴当m=50时，w最大=5000即当工厂每天消耗50千度电时，工厂每天消耗电产生利润最大为5000元.
解题步骤：1.分析题意，把实际问题转化为数学问题，画出图形.2.根据已知条件建立适当的平面直角坐标系.3.选用适当的解析式求解.4.根据二次函数的解析式解决具体的实际问题.