2021年中考数学二轮复习：反比例函数专题练习（Word版无答案）

这是一份2021年中考数学二轮复习：反比例函数专题练习（Word版无答案），共9页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
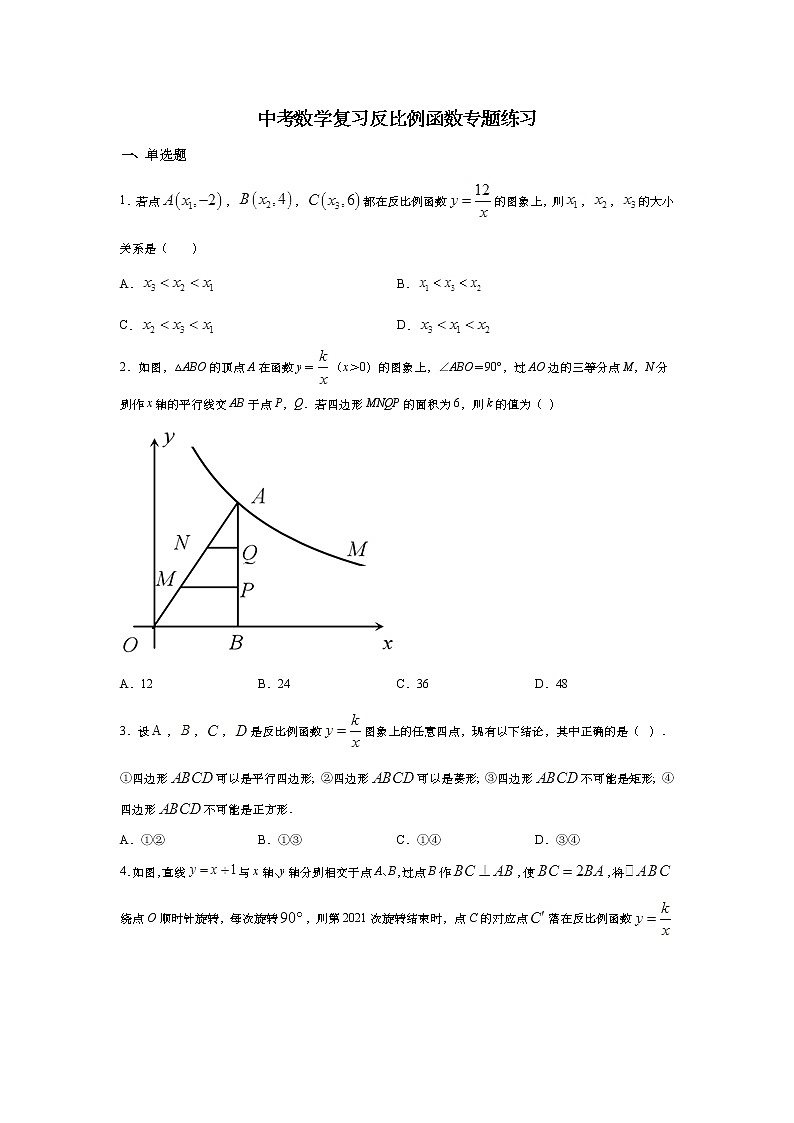
中考数学复习反比例函数专题练习 一、单选题1．若点，，都在反比例函数的图象上，则，，的大小关系是（　　）A． B．C． D．2．如图，△ABO的顶点A在函数y＝（x＞0）的图象上，∠ABO＝90°，过AO边的三等分点M，N分别作x轴的平行线交AB于点P，Q．若四边形MNQP的面积为6，则k的值为（ ）
 A．12 B．24 C．36 D．483．设，，，是反比例函数图象上的任意四点，现有以下结论，其中正确的是（   ）．
①四边形可以是平行四边形；②四边形可以是菱形；③四边形不可能是矩形；④四边形不可能是正方形．A．①② B．①③ C．①④ D．③④4．如图，直线与x轴、y轴分别相交于点A、B，过点B作，使，将绕点O顺时针旋转，每次旋转，则第2021次旋转结束时，点C的对应点落在反比例函数的图象上，则k的值为（   ）
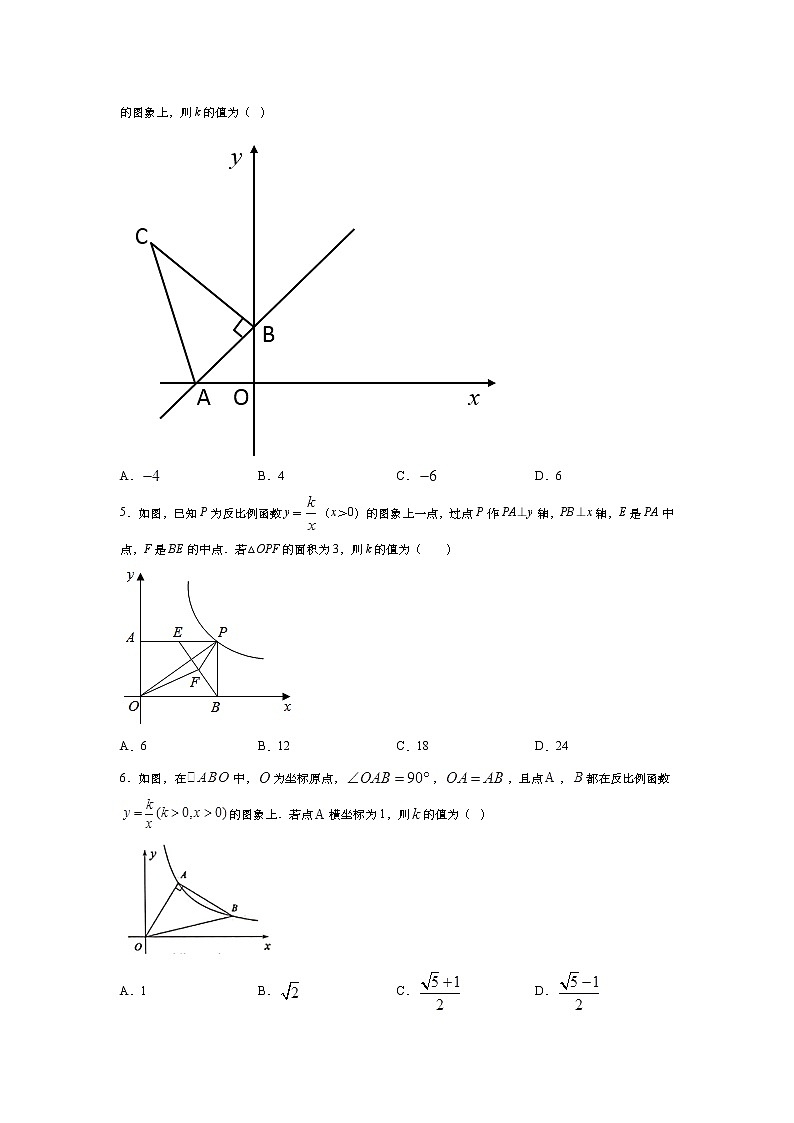
 A． B．4 C． D．65．如图，已知P为反比例函数y＝（x＞0）的图象上一点，过点P作PA⊥y轴，PB⊥x轴，E是PA中点，F是BE的中点．若△OPF的面积为3，则k的值为（　　）
 A．6 B．12 C．18 D．246．如图，在中，为坐标原点，，，且点，都在反比例函数的图象上．若点横坐标为1，则的值为（   ）
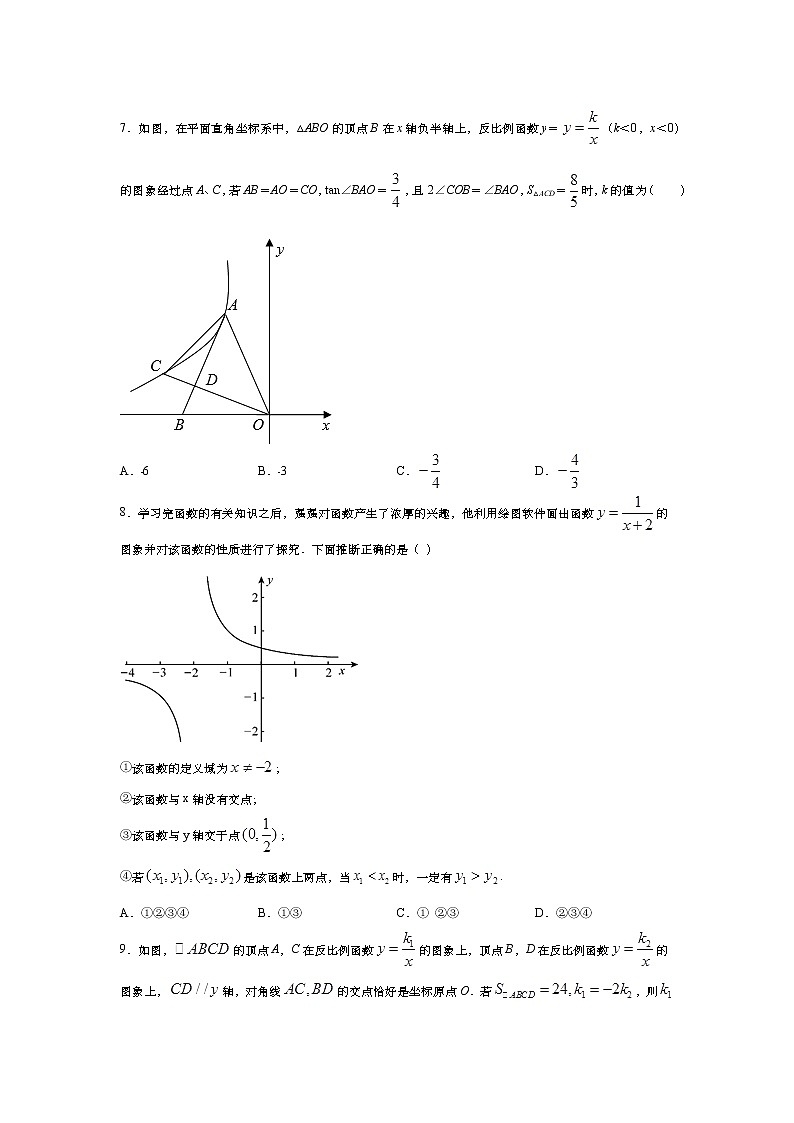
 A．1 B． C． D．7．如图，在平面直角坐标系中，△ABO的顶点B在x轴负半轴上，反比例函数y＝（k＜0，x＜0）的图象经过点A、C，若AB＝AO＝CO，tan∠BAO＝，且2∠COB＝∠BAO，S△ACD＝时，k的值为（　　）
 A．﹣6 B．﹣3 C． D．8．学习完函数的有关知识之后，强强对函数产生了浓厚的兴趣，他利用绘图软件画出函数的图象并对该函数的性质进行了探究．下面推断正确的是（  ）

①该函数的定义域为；   
②该函数与x轴没有交点；  
③该函数与y轴交于点； 
④若是该函数上两点，当时，一定有.A．①②③④ B．①③ C．① ②③ D．②③④9．如图，的顶点A，C在反比例函数的图象上，顶点B，D在反比例函数的图象上，轴，对角线的交点恰好是坐标原点O．若，则的值为（   ）
 A． B． C． D．10．反比例函数 的图象如图，点是该函数图象上一点，轴，垂足是点，如果，则的值为（   ）
 A．3 B．-3 C．6 D．-611．如图是个台阶的示意图，每个台阶的高和宽分别是1和2，每个台阶凸出的角的顶点记作（m为1～8的整数）．函数的图象为曲线L．若曲线L使得这些点分布在它的两侧，每侧各4个点，则k的取值范围为（   ）
 A． B． C． D．12．如图，点A为反比例函数图象上的一点，过点A作轴于点B，点C为x轴上的一个动点，的面积为3，则k的值为（）
 A．3 B．6 C．9 D．12 二、填空题13．我们把反比例函数图象上到原点距离相等的点叫做反比例函数图象上的等距点．如果第一象限内点A（2，4）与点B是某反比例函数图象上的等距点，那么点A、B之间的距离是_____．14．如图，在平面直角坐标系中，正比例函数y＝kx与反比例函数的图象相交于A，B两点，过点A作y轴的垂线交y轴于点C，连接BC，则△ABC的面积是_____．
 15．如图，正方形ACBE的边长是，点B，C分别在x轴和y轴正半轴上，，轴于点D，ED的中点F在反比例函数的图象上．则_________．
 16．如图，在平面直角坐标系中，菱形ABCD在第一象限内，边BC与x轴平行，A，B两点的纵坐标分别为5，1，反比例函数y＝的图象经过A，B两点，菱形ABCD的周长为20，则k的值为_____．
 17．如图，平面直角坐标系xOy中，正方形ABCO的顶点A，C分别在x轴和y轴的正半轴上，反比例函数y＝ （x＞0）的图象分别与边BC，AB交于点D和点E，连接OD，EF∥OD交OA于点F，若OF＝2FA，且OD＝k，则k的值为_____．
 18．如图，点A在反比例函数y＝（k≠0）的图象上，点B在x轴的负半轴上，直线AB与y轴交于点C，若＝，AOB的面积为18，则k的值为___．
 19．如图，在平面直角坐标系中，已知菱形OABC，点A的坐标为（3，0），点B，C均在第一象限，反比例函数y＝（x＞0）的图象经过点C，且与边AB交于点D，若D是AB的中点，则k的值为_____．
 20．如图，在直角坐标系中，菱形ABCD的顶点C与原点O重合，点B在y轴的正半轴上，点A在双曲线y＝（x＞0）上，点D的坐标为（4，3）．若将菱形ABCD向右平移，使点D恰好落在此双曲线上，那么菱形平移的距离为_____．
  三、解答题21．如图，在平面直角坐标系中，，是反比例函数的图象上的两点，以为边作正方形，点，分别在轴、轴的正半轴上，点的坐标为，且．

（1）求的值；
（2）求所在直线的解析式．22．如图，在平面直角坐标系xOy中，菱形ABCD的顶点B的坐标为（1，0），顶点A的坐标为（，2），对角线AC∥x轴，边BC所在直线与反比例函数的图象交于C，E两点．
（1）求和的函数解析式；
（2）点P是x轴上一动点，当△PAC是以AC为斜边的直角三角形时，请求出点P的坐标．
 23．如图，一次函数的图象与反比例函数的图象交于点和．过A作轴于C，交OB于E，且．
（1）求一次函数和反比例函数解析式；
（2）当x为何值时，；
（3）若点P是线段AB的中点，求的面积．
 24．希腊数学家帕普斯给出了一种“三等分锐角”的方法，具体如下：
①建立平面直角坐标系，将已知锐角∠AOB的顶点与原点O重合，角的一边OB与x轴正方向重合；
②在平面直角坐标系中，绘制函数的图象，图象与已知角的另一边OA交于点P；
③以P为圆心，2OP为半径作弧，交函数的图象于R点；
④分别过点P和R作x轴和y轴的平行线，两线相交于点M、Q；
⑤连接OM，得到∠MOB，这时∠MOB＝∠AOB．
根据以上材料解答下列问题：
（1）设点P的坐标为（a，），点R的坐标为（b，），则点M的坐标为　  　；
（2）求证：点Q在直线OM上；
（3）求证：∠MOB＝∠AOB．