2020-2021学年四 多边形的面积综合与测试教案及反思

这是一份2020-2021学年四 多边形的面积综合与测试教案及反思，共8页。教案主要包含了教学内容，教学目标，教学重点，教学难点，教具学具，教学过程，板书设计等内容，欢迎下载使用。
【教学内容】
北师大版小学数学五年级上册第四单元第61、62页
【教学目标】
1、进一步理解并掌握平行四边形、三角形和梯形的面积公式，能应用公式计算这些图形的面积，并解决一些简单的实际问题。
2、引导、鼓励学生借助图形操作，沟通三个图形面积之间的关系，运用公式，从新旧联系、运动变化以及等积变形三个维度，分析内在联系，在知识上求联、在方法上求通，激发学生探究的兴趣，提升了学生探究水平与思维。
3、结合练习，加深对所学知识的理解，提高应用所学知识解决实际问题的能力，逐步形成自己整理所学知识的意识和良好的学习习惯。
【教学重点】
归纳整理本单元所学的面积计算公式及推导过程，会解决实际问题。
【教学难点】
沟通三个图形面积之间的关系，运用公式，从新旧联系、运动变化以及等积变形三个维度，分析内在联系。
【教具学具】
多媒体课件，平行四边形、梯形、三角形卡片。
【教学过程】
一 回忆梳理，引入新知
1师：五一劳动节快要到了，学校要用红、黄、蓝三种颜色的彩纸做背景，在上面粘贴纪律小明星的照片。每个区域大约粘贴多少张？
师小结：看来，学会平面图形的面积计算方法可以帮助我们解决生活中的一些实际问题，这节课我们就一起来对它们的面积计算公式进行回顾和复习。
2师：回忆一下：本单元学习了哪些多边形的面积？
3师：多边形分为两类：基本图形与组合图形，像长方形、平行四边形、三角形、梯形这种利用公式直接求出面积的图形,我们称它们为基本图形，与之相对应的是组合图形，是由若干个基本图形组成的。这节课，重点对平行四边形、三角形、梯形的面积进行复习。
二 沟通联系，融会贯通
1出示小组合作要求，小组合作学习
小组合作要求：
（1）平行四边形、三角形、梯形的面积计算公式是什么？
（2）这些平面图形的面积计算公式是怎样推导出来的？请各小组借助手中的学具卡片进行演示并说一说。
（3）想一想这些面积公式的推导有怎样的联系呢？用你喜欢的方法表示出来。能整理成知识网络吗？
2小组汇报，总结知识网络图，找到新旧知识之间的联系
师：在推导的过程中用到了哪些方法？（割补法 平移法 拼接法）
师：能不能说三角形是平行四边形的一半？
形成思维网络图：
S=ab
S=ah÷2
S=(a+b)h÷2
a
b
S=ah
a
h
a
h
a
b
h
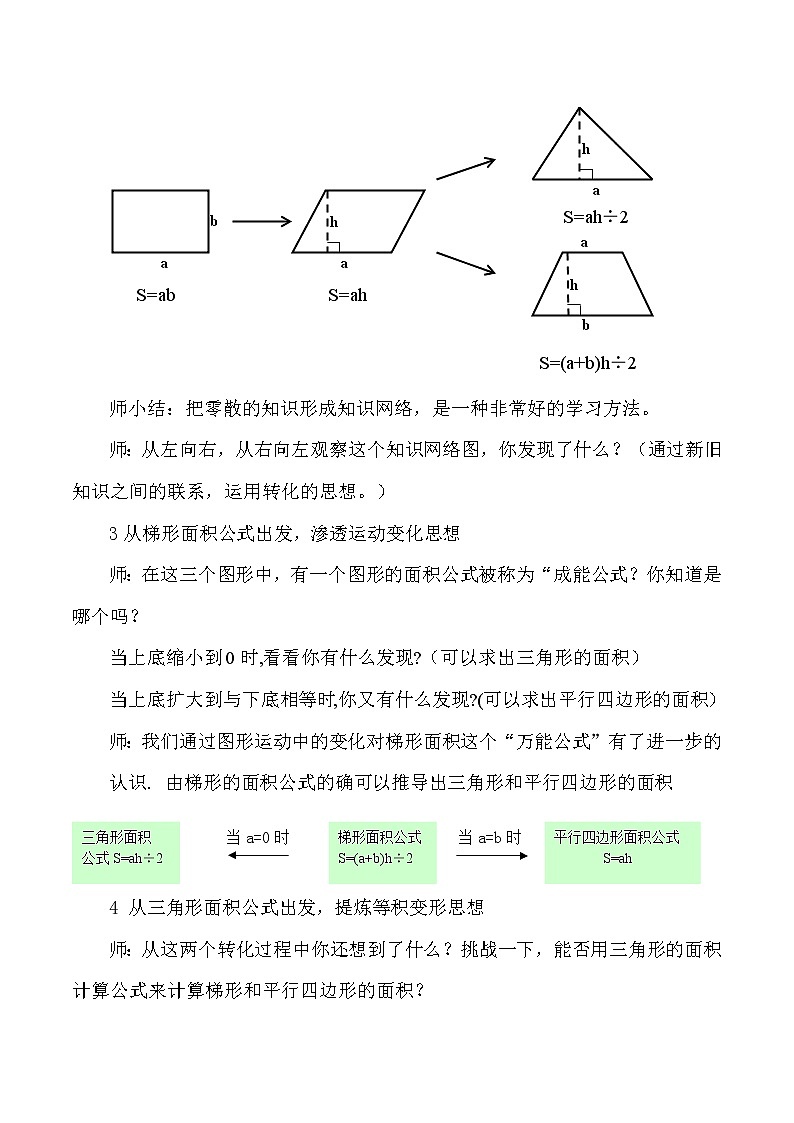
师小结：把零散的知识形成知识网络，是一种非常好的学习方法。
师：从左向右，从右向左观察这个知识网络图，你发现了什么？（通过新旧知识之间的联系，运用转化的思想。）
3从梯形面积公式出发，渗透运动变化思想
师：在这三个图形中，有一个图形的面积公式被称为“成能公式？你知道是哪个吗？
当上底缩小到0时,看看你有什么发现?（可以求出三角形的面积）
当上底扩大到与下底相等时,你又有什么发现?(可以求出平行四边形的面积）师：我们通过图形运动中的变化对梯形面积这个“万能公式”有了进一步的认识. 由梯形的面积公式的确可以推导出三角形和平行四边形的面积.
当a=0时
三角形面积
公式S=ah÷2
平行四边形面积公式
S=ah
梯形面积公式
S=(a+b)h÷2
当a=b时
4 从三角形面积公式出发，提炼等积变形思想
师：从这两个转化过程中你还想到了什么？挑战一下，能否用三角形的面积计算公式来计算梯形和平行四边形的面积？
出示学习要求：
（1）分一分：把梯形和平行四边形分成几个三角形？
（2）算一算：请用字母表示分成的三角形，并算一算。
（3）想一想：能不能把分成的多个三角形变成一个三角形？
（生独立探究）
（预设：先把梯形分成两个三角形，于是这个梯形的面积就变成了两个三角形的面积，一个三角形的面积是 ah÷2，另一个三角形是 bh÷2，合在一起就是 ah÷2+bh÷2=（a÷b）h÷2。）
师：能否把两个三角形变成一个大三角形呢？
师小结：同学们发现了吗？图形形状发生了变化，面积没有发生变化，我们称之为——等积变形。有没有同学想到平行四边形是怎么变的呢？
（先把平行四边形沿对角线分成两个三角形，把其中一个三角形翻转，然后等积变形成这样的三角形。三角形的底就是原平行四边形的底的两倍，三角形的高就是原平行四边形的高。）
5小结方法，沟通联系
师小结：知识之间的联系多么紧密啊！三个面积计算公式可以通过新旧之间的联系转化成平行四边形面积计算公式，通过运动变化的方法转化成梯形的面积计算公式，还可以通过等积变形转化成三角形的面积计算公式。你还知道哪些知识与我们今天复习的知识有联系呢？
三 层次练习，应用提升
1每张照片大约用2平方分米，每个区域大约能粘贴几张照片？
师：在计算的时候要注意什么？（1求三角形与梯形的面积时要除以2，
2对应底乘对应高。）
2 一个直角三角形的面积是90平方厘米，一条直角边长9厘米，另一条直角边长多少？
师：说清思路（1算术方法，2解方程）为什么不能忘记乘2？
3教材61页第1题：下图中每个小方格的边长表示1厘米。
（1）说一说，图中哪两个图形的面积相等？你是通过什么方法知道的？
（2）哪两个图形可以拼成平行四边形？
预设的方法：
A数方格 (通用)
B公式法 (通用)
C重叠法 图1到图3,图5到图7,先旋转,平移,重叠比较
D割补法 图5和图7都可割补成一个2×2的正方形或4×2÷2的直角三角形.
E观察目测 根据等底等高的三角形面积相等判断图1图3和图5面积相等。
师追问:面积相等的两个三角形一定等底等高吗?如果用图中的三角形来解释三角形面积的计算方法？你选择哪两个三角形?
4在平行四边形中画一个最大的三角形,你有什么发现?
平行四边形与梯形及一般四边形中的一半模型：
师：图中的阴影部分占所在四边形面积的一半，这在平面几何中叫一半模型。
不仅在平行四边形,在梯形及至任意四边形都有一半模型。这些阴影部分都是它所在四边形面积的一半，感兴趣的同学可以用刚刚复习到的方法在课下推导一下。一半模型,它是平面几何中最重要的地基模型,将来你还会由此学到蝴蝶模型,燕尾模型,鸟头模型.,沙漏模型等。
5求每一部分的占地面积及摆放盆数。
师小结：求一串红与蝴蝶花两种方法 (1面积公式，2拼接成长方形)
求菊花 (常规方法:1整体--部分2一半模型)
6用篱笆围成一个梯形养鸡场,其中一边利用房屋墙壁,已知篱笆长80m，求养鸡场的占地面积。
师小结：由此我们又得出了一条重要的数学思想：要敢于抛弃原有的固定思维模式，善于寻找“另类”的方法。
四 总结全课 畅谈收获
1师：这节课你有哪些收获呢？
2师总结：在这节课中，我们通过新旧转化,运动变化,等积变形等思想,加深了对于各种平面图形面积公式的理解。知识之间有着千丝万缕的联系,我们要在总结中反思,在对比中发现,这样数学才能越学越活，越学越有意义。
【板书设计】