北师大版七年级下册2 频率的稳定性优秀ppt课件

这是一份北师大版七年级下册2 频率的稳定性优秀ppt课件，文件包含北师大版七年级数学下册622用频率估计概率课件pptx、北师大版七年级数学下册622用频率估计概率docx等2份课件配套教学资源，其中PPT共24页， 欢迎下载使用。

1．理解当事件的试验结果不是有限个，或各种可能结果发生的可能性不相等时，要用频率来估计概率，进一步发展概率观念。2．进一步理解概率与频率之间的联系与区别，培养学生根据频率集中趋势估计概率的能力。
必然事件∶在一定条件下重复进行试验时，在每次试验中必然会发生的事件。不可能事件∶在一定条件下重复进行试验时，在每次试验中不可能发生的事件。随机事件∶在一定条件下，可能发生也可能不发生的事件.也可称为偶然性事件。特征∶事先不能预料，即具有不确定性
一般地，对于一个事件A，把刻画其发生可能性大小的数值，称之为事件A发生的概率。记为P（A）概率从数量上刻画了一个随机事件发生的可能性的大小。
必然事件发生的概率为1；不可能事件发生的概率为0； 随机事件A发生的概率P(A)是0与1之间的一个常数.
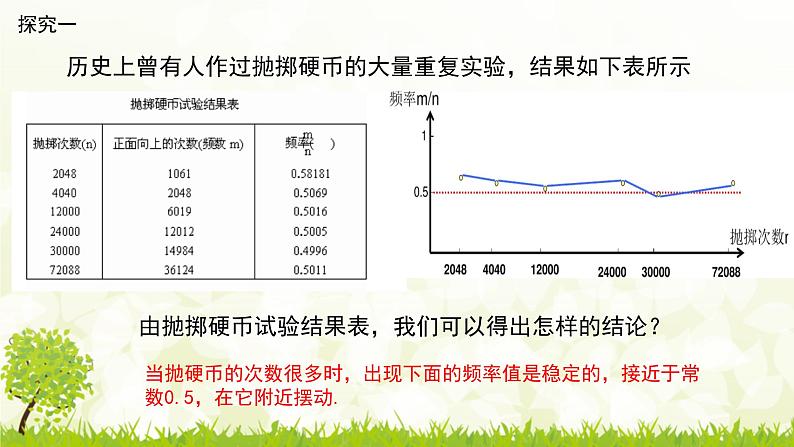
历史上曾有人作过抛掷硬币的大量重复实验，结果如下表所示
由抛掷硬币试验结果表，我们可以得出怎样的结论？
当抛硬币的次数很多时，出现下面的频率值是稳定的，接近于常数0.5，在它附近摆动.
某批乒乓球质量检查结果表
当抽查的球数很多时，抽到优等品的频率 ，接近于常数0.95，在它附近摆动。
某种油菜籽在相同条件下的发芽试验结果表
当试验的油菜籽的粒数很多时，油菜籽发芽的频率 接近于常数0.9，在它附近摆动。
一般地，在大量重复试验中，如果事件A发生的频率稳定于某个常数p，可以估计这个事件发生的概率,那么事件A发生概率的概率
温馨提示：通常我们用频率估计出来的概率要比频率保留的数位要少。
在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20个，某学习小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复．下表是活动进行中的一组统计数据：
（1）补全上表中的有关数据；（2）请估计：当n很大时，摸到白球的频率将会接近______（保留两位小数）（3）试估算口袋中白球的个数.
解：（3）因为当n很大时，摸到白球的频率将会接近0.6，所以白球的个数=0.6×20=12（个）.
在一个不透明的盒子里装有黑、白两种颜色的球共40只，这些球除颜色外其余完全相同.小颖做摸球实验，搅匀后，她从盒子里随机摸出一只球记下颜色后，再把球放回盒子中，不断重复上述过程，下表是实验中的一组统计数据：
(1)请估计：当n很大时，摸到白球的频率将会接近______；(精确到0.1)(2)若从盒子里随机摸出一只球，则摸到白球的概率的估计值为_____；(3)试估算盒子里黑、白两种颜色的球各有多少只.
解：(3)盒子里白球有40×0.6=24(只)，黑球有40-24=16（只）.
小颖和小红两位同学在学习"概率"时，做投掷骰子（质地均匀的正方体）试验，她们共做了60次试验，试验的结果如下表∶
（1）计算"3点朝上"的频率和"5点朝上"的频率;（2）小颖说∶"根据试验，一次试验中出现5点朝上的概率最大"。小红说∶"如果投掷600次，那么出现6点朝上的次数正好是100次"小颖和小红的说法正确吗?为什么?
在一个不透明的袋中有除颜色外其他完全相同的3个球，每次从袋中摸出一个球，记下颜色后放回搅匀再摸，在摸球试验中得到下表中部分数据：
(1)请将上表补充完整(结果精确到1%)；(2)制作折线统计图表示摸到黄球的频率的变化情况；(3)估计从袋中摸出一个球是黄球的概率是多少．
小明抛硬币的过程(每枚硬币只有正面朝上和反面朝上两种情况)见下表，阅读并回答问题：
(1)从表中可知，当抛完10次时正面出现3次，正面出现的频率为30%，那么，小明抛完10次时，得到　　次反面，反面出现的频率是　 　；(2)当他抛完5000次时，反面出现的次数是　 　，反面出现的频率是　 　；(3)通过上表我们可以知道，正面出现的频数和反面出现的频数之和等于 　，正面出现的频率和反面出现的频率之和等于　　.
如图，广宇购物中心设立了一个可以自由转动的转盘，并规定：顾客购物满20元以上就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应的奖品，下表是活动进行中的一组统计数据．
(1)计算并完成上面的表格；(2)请估计，当n很大时，频率将会接近多少？(3)假如你去转动该转盘一次，你获得牙膏的概率是多少？
概率与频率之间的区别和联系∶区别∶频率是个试验值，试验结果不相同频率也就不相同，频率只能近似地反映事件发生的可能性的大小;而概率是一个理论值，是由事件的本质决定的，其大小是个固定值，概率能精确的反映事件发生的可能性的大小。联系∶可以通过大量的重复试验，用一个随机事件发生的频率去估计它的概率。