数学八年级下册第十八章 平行四边形18.2 特殊的平行四边形18.2.1 矩形集体备课课件ppt

这是一份数学八年级下册第十八章 平行四边形18.2 特殊的平行四边形18.2.1 矩形集体备课课件ppt，共30页。PPT课件主要包含了温故而知新，细心观察，学习新知，动手试一试，比一比知关系，学以致用，学有所得，学例题知方法，试一试你能行，∴BC7等内容，欢迎下载使用。

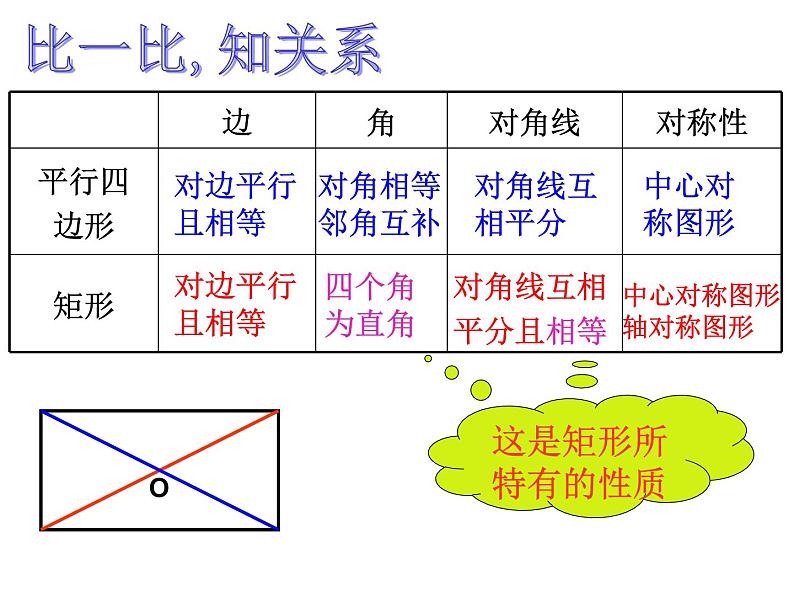
平行四边形有哪些性质？
细心观察平行四边形内角的变化
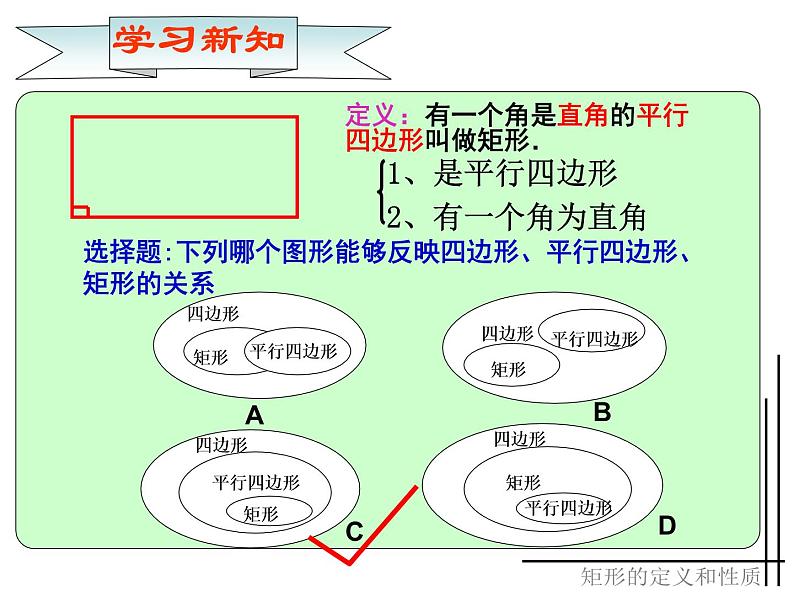
定义：有一个角是直角的平行四边形叫做矩形．
选择题:下列哪个图形能够反映四边形、平行四边形、矩形的关系
1、平行四边形变成矩形时，图形的内角有何特征？2、平行四边形变成矩形时，两条对角线的长度有什么关系？
在操作过程中,请你思考下列问题:
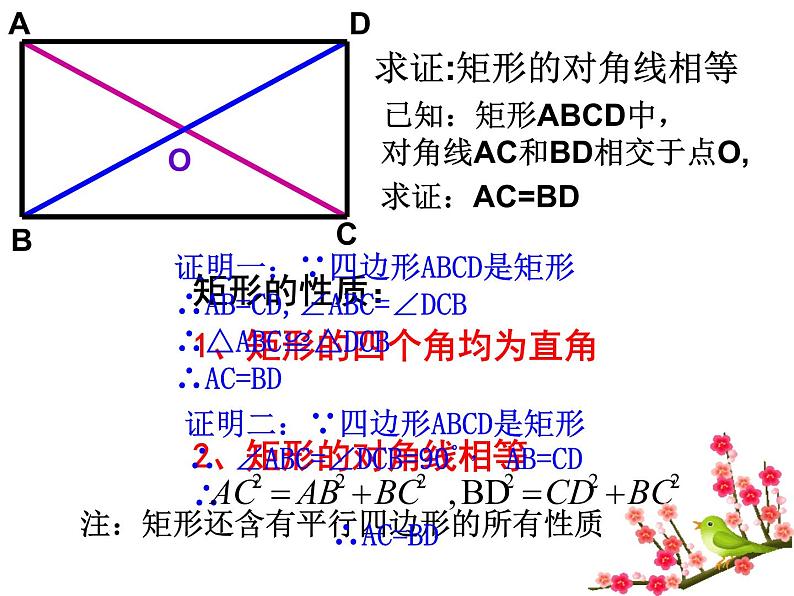
求证:矩形的对角线相等
已知：矩形ABCD中， 对角线AC和BD相交于点O,
矩形的性质：1、矩形的四个角均为直角2、矩形的对角线相等
注：矩形还含有平行四边形的所有性质
证明一：∵四边形ABCD是矩形∴AB=CD,∠ABC=∠DCB∴△ABC≌△DCB ∴AC=BD
中心对称图形轴对称图形
1. 矩形具有而一般平行四边形不具有的性质是（ ）. A、对角线相等 B、对边相等 C、对角相等 D、对角线互相平分
2、 矩形的一组邻边长分别是3cm和4cm，则它的对角线长是 cm.
直角三角形的性质:直角三角形斜边上的中线等于斜边的一半.
即兴练一练:已知一直角三角形两直角边分别为6和8,则其斜边上的中线长为________.
图中我们常见的特殊三角形有哪些？
解：∵四边形ABCD是矩形，∴AC与BD相等且互相平分.
又∵∠AOB=60°，
∴OA=AB=4（cm）∴矩形的对角线AC=BD=2OA=8 ( cm ) .
∴△AOB是等边三角形
已知: 如图，矩形ABCD的两条对角线交于点O, AB= 4cm ，∠AOB=60°。求矩形对角线的长。
1、如图，矩形ABCD的对角线的长为2，∠BDC=300,则矩形ABCD的面积为______.2、矩形两条对角线所夹的锐角为60°,较短的边长为3.6cm,则对角线的长为_____cm.
3、矩形ABCD中,AC、BD相交于点O，AB=6，BC=8，则△ABO的周长为_____
1、如图，矩形ABCD中，AE平分∠BAD交BC于点E，ED=5cm,EC=3cm,求矩形的周长。
解：∵四边形ABCD是矩形∴∠C＝∠B=∠BAD=90°,AB=DC
注:解决矩形的有关问题时,常根据性质转化为直角三角形的有关问题进行解答.
∵DE=5,EC=3∴DC2=DE2-EC2=52-32,即：DC=4
∵AE平分∠BAD∴∠BAE=45°
∴矩形ABCD的周长为22cm
今天的收获……你还有什么不明白的地方……
4、在矩形中进行有关计算或证明，常根据矩形的性质将问题转化到直角三角形或等腰三角形中，利用直角三角形或等腰三角形的有关性质 进行解题。
3、直角三角形的一个重要性质：斜边上的中线等于斜边的一半；
1、矩形定义：有一个角是直角的平行四边形叫矩形
矩形的对边平行且相等矩形的四个角均为直角
矩形的对角线互相平分且相等
作 业
1.矩形具有而一般平行四边形不具有的性质是（ ） A.对角线相等 B.对边相等 C.对角相等 D.对角线互相平分
2.下面性质中，矩形不一定具有的是（ ） A.对角线相等 B.四个角相等 C.是轴对称图形 D.对角线互相垂直
已知矩形ABCD,请找出所有的直角三角形和等腰三角形.
矩形的问题可以转化到直角三角形或等腰三角形来解决．
Rt△ADC、 Rt△DCB、Rt△DAB、 Rt△ABC、
△ADO、 △DOC、△COB、 △AOB、
如图，矩形ABCD的两条对角线相交于点Ｏ，AB=4cm,∠AOB=60°,求矩形对角线的长。
解：∵四边形ABCD是矩形，
∴AC与BD相等且互相平分。
又 ∠AOB=60°，
∴ ΔOAB是等边三角形
∴OA=AB=4（cm）
∴ AC=BD = 2OA=2×4=8（cm）
变式：若BD=8cm,∠AOD=120°，求边AB的长。
公平,因为OB=OD = OA=OC
生活链接---投圈游戏
OB=OD = OA=OC
推论：直角三角形斜边上的中线等于 斜边的一半。
= AC= BD
在 中，∠ABC=900 ，
BO是斜边AC上的中线
1. 已知△ABC是Rt△,∠ABC=900,BD是斜边AC上的中线.
(1)若BD=3㎝,则AC＝______ ㎝;(2)若∠C=30°,AB＝5㎝,则AC＝_____㎝, BD＝_____㎝.
2.在 中，斜边AC上的中线和高分别是6cm和5cm，则 的面积S=（ ）。
3.在Rt⊿ABC中，∠C=90°，AB=2AC.求∠ A 、 ∠B 的度数.
∴⊿ACD是等边三角形
∴∠A=60° ∴∠B=30 °
4.矩形ABCD中,AB=2BC,AE=AB,求∠EBC的度数
5.设矩形ABCD和矩形AEFC的面积分别为S1、S2，则二者的大小关系是：S1________S2．
6.已知如图，O是矩形ABCD对角线的交点，AE平分∠BAD，∠AOD=1200，求∠EAO的度数和∠OEA的度数 。
7.已知：如图，在四边形ABCD中，∠ABC=∠ADC=900，M是AC的中点，N是
（1）试判断MD与MB的大小关系。（2）试判断MN与BD的位置关系。
2、如图，矩形AEFG和矩形ADCB的大小、形状完全相同，把它们拼成如图所示的L型图案，已知∠FAE=30°,分别求∠1、∠2的度数。
解:依题意可知:∠FAE=∠DCA=30 °,AF=AC
∴∠2=∠ACF-∠ACD=15 °
∴∠DAC=60 °,
∴∠FAC=90 °,