苏教版 (2019)选择性必修第一册第5章 导数及其应用5.3 导数在研究函数中的应用导学案

这是一份苏教版 (2019)选择性必修第一册第5章 导数及其应用5.3 导数在研究函数中的应用导学案，共8页。

如果函数f(x)在区间(a，b)上是增函数，那么对任意的x1，x2∈(a，b)，当x10.这表明，函数的平均变化率与其单调性密切相关．进一步猜想，函数的瞬时变化率(即导数)与其单调性也密切相关．
[问题] 导数与函数的单调性有什么联系？



知识点 函数的单调性与其导数正负的关系
对于函数y＝f(x)：
(1)如果在某区间上f′(x)>0，那么f(x)为该区间上的eq \a\vs4\al(增)函数；
(2)如果在某区间上f′(x)0，则f(x)仍为增函数(减函数的情形完全类似)；
(2)f(x)为增函数的充要条件是对任意的x∈(a，b)都有f′(x)≥0且在(a，b)内的任一非空子区间上f′(x)不恒为0.
在区间(a，b)内，若f′(x)>0，则f(x)在此区间上单调递增，反之也成立吗？
提示：不一定成立．比如y＝x3在R上为增函数，但其在x＝0处的导数等于零．也就是说f′(x)>0是y＝f(x)在某个区间上单调递增的充分不必要条件．
1．函数f(x)＝(x－3)ex的单调递增区间是( )
A．(－∞，2) B．(0，3)
C．(1，4) D．(2，＋∞)
答案：D
2．函数f(x)＝2x－sin x在(－∞，＋∞)上( )
A．是增函数
B．是减函数
C．在(0，＋∞)上单调递增，在(－∞，0)上单调递减
D．在(0，＋∞)上单调递减，在(－∞，0)上单调递增
答案：A
3.如图为导函数y＝f′(x)的图象，则函数y＝f(x)的单调区间是什么？
解：单调递增区间：(－∞，－3]，[－2，1]，[3，＋∞)；
单调递减区间：[－3，－2]，[1，3]．
角度一：根据原函数图象确定导函数图象
[例1] 已知函数y＝f(x)的图象如图所示，则函数y＝f′(x)的图象可能是图中的( )
[解析] 由函数y＝f(x)的图象的增减变化趋势判断函数y＝f′(x)的正、负情况如下表：
由表可知函数y＝f′(x)的图象，当x∈[－1，b)时，在x轴下方；当x∈[b，a)时，在x轴上方；当x∈[a，1]时，在x轴下方．故选C.
[答案] C
eq \a\vs4\al()
对于原函数图象，要看其在哪个区间内单调递增，则在该区间内导数值大于零．在哪个区间内单调递减，则在此区间内导数值小于零．根据导数值的正负可判定导函数图象．
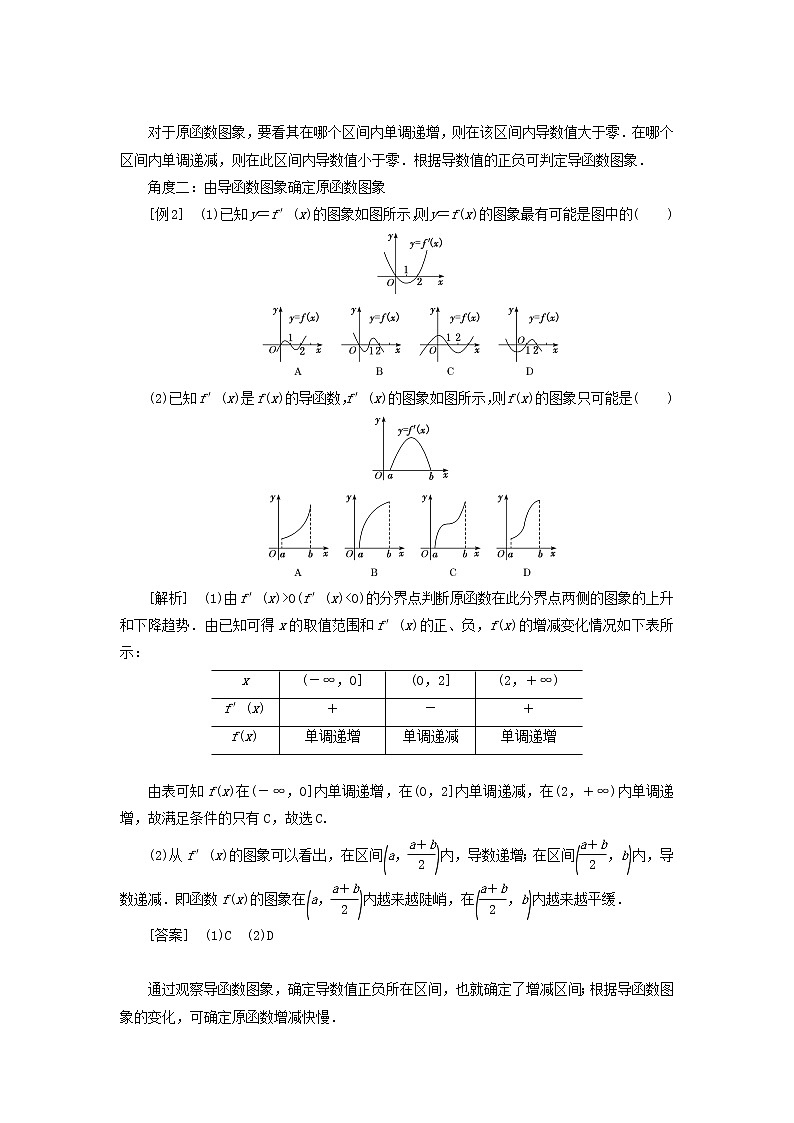
角度二：由导函数图象确定原函数图象
[例2] (1)已知y＝f′(x)的图象如图所示，则y＝f(x)的图象最有可能是图中的( )
(2)已知f′(x)是f(x)的导函数，f′(x)的图象如图所示，则f(x)的图象只可能是( )
[解析] (1)由f′(x)>0(f′(x)0时，f′(x)的符号变化依次为＋，－，＋.故选C.
2．已知y＝xf′(x)的图象如图所示(其中f′(x)是函数f(x)的导函数)，下面四个图象中，y＝f(x)的图象大致是( )
解析：选C 当 00得x>eq \f(\r(3),3)，
令f′(x)