2020-2021学年北师大新版九年级上册数学期末复习试卷2（Word版 含解析）

这是一份2020-2021学年北师大新版九年级上册数学期末复习试卷2（Word版 含解析），共20页。试卷主要包含了对于二次函数y＝2，把函数y＝，小亮根据x的取值等内容，欢迎下载使用。
1．已知线段c为线段a，b的比例中项，若a＝1，b＝2，则c＝（ ）
A．1B．C．D．
2．对于二次函数y＝2（x﹣1）2﹣8，下列说法正确的是（ ）
A．图象开口向下
B．当x＞1时，y随x的增大而减小
C．当x＜1时，y随x的增大而减小
D．图象的对称轴是直线x＝﹣1
3．如图是某兴趣社制作的模型，则它的俯视图是（ ）
A．B．C．D．
4．某纪念品原价150元，连续两次涨价a%后售价为216元．下列所列方程中正确的是（ ）
A．150（1+2a%）＝216
B．150（1+a%）×2＝216
C．150（1+a%）2＝216
D．150（1+a%）+150（1+a%）2＝216
5．小明在太阳光下观察矩形窗框的影子，不可能是（ ）
A．平行四边形B．长方形C．线段D．梯形
6．把函数y＝（x﹣1）2+2图象向右平移1个单位长度，平移后图象的函数解析式为（ ）
A．y＝x2+2B．y＝（x﹣1）2+1C．y＝（x﹣2）2+2D．y＝（x﹣1）2+3
7．一商家进行促销活动，某商品的优惠措施是“第二件商品半价”．现购买2件该商品，相当于这2件商品共打了（ ）
A．5 折B．5.5折C．7折D．7.5折
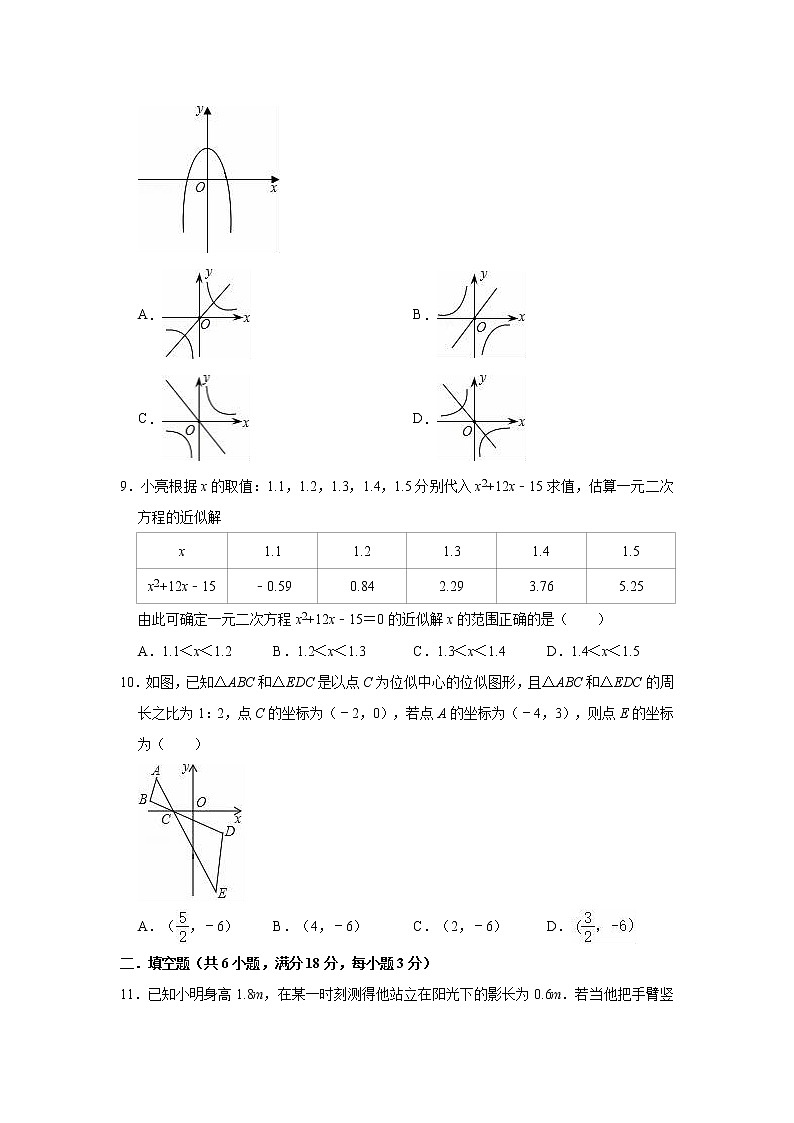
8．二次函数y＝ax2+c的图象如图所示，正比例函数y＝ax与反比例函数y＝在同一坐标系中的图象可能是（ ）
A．B．
C．D．
9．小亮根据x的取值：1.1，1.2，1.3，1.4，1.5分别代入x2+12x﹣15求值，估算一元二次方程的近似解
由此可确定一元二次方程x2+12x﹣15＝0的近似解x的范围正确的是（ ）
A．1.1＜x＜1.2B．1.2＜x＜1.3C．1.3＜x＜1.4D．1.4＜x＜1.5
10．如图，已知△ABC和△EDC是以点C为位似中心的位似图形，且△ABC和△EDC的周长之比为1：2，点C的坐标为（﹣2，0），若点A的坐标为（﹣4，3），则点E的坐标为（ ）
A．（，﹣6）B．（4，﹣6）C．（2，﹣6）D．
二．填空题（共6小题，满分18分，每小题3分）
11．已知小明身高1.8m，在某一时刻测得他站立在阳光下的影长为0.6m．若当他把手臂竖直举起时，测得影长为0.78m，则小明举起的手臂超出头顶 m．
12．关于x的一元二次方程x2﹣x﹣1＝0有两个不相等的实数根，则k的取值范围为 ．
13．如图，在矩形ABCD中，AD＞AB，AB＝2．点E在矩形ABCD的边BC上，连结AE，将矩形ABCD沿AE翻折，翻折后的点B落在边AD上的点F处，得到矩形CDFE．若矩形CDFE与原矩形ABCD相似，则AD的长为 ．
14．如图，将△ABC沿BC方向平移得到△A'B'C'，△ABC与△A'B'C'重叠部分（即图中阴影部分）的面积是△ABC面积的，若，则△ABC平移的距离BB'是 ．
15．某公园准备围建一个矩形花园ABCD，其中一边靠墙，其他三边用长为54米的篱笆围成，已知墙EF长为28米，并且与墙平行的一面BC上要预留2米宽的入口（如图MN所示，不用围篱笆），若花园的面积为320平方米，则AB＝ ．
16．如图，矩形ABCD中，AB＝4，AD＝6，点E是边CD上一点，EF⊥AE交BC于点F，则CF长的取值范围是 ．
三．解答题（共3小题，满分22分）
17．用公式法解方程：x2+4x﹣5＝0．
18．计算：（﹣2）﹣2﹣|﹣2|+（﹣）0﹣﹣2cs30°．
19．三辆汽车经过某收费站下高速时，在2个收费通道A，B中，可随机选择其中的一个通过．
（1）一辆汽车经过此收费站时，选择A通道通过的概率是 ；
（2）求三辆汽车经过此收费站时，至少有两辆汽车选择B通道通过的概率．（请用画树状图的方法写出分析过程，并求出结果）．
四．解答题（共2小题，满分16分，每小题8分）
20．如图，∠ACB＝∠ADC＝90°，AC＝，AD＝2．问当AB的长为多少时，这两个直角三角形相似．
21．阅读下面材料：
在数学课上，老师提出如下问题：
已知：如图，四边形ABCD是平行四边形；
求作：菱形AECF，使点E，F分别在BC，AD上．
小凯的作法如下：
（1）连接AC；
（2）作AC的垂直平分线EF分别交BC，AD于E，F．
（3）连接AE，CF
所以四边形AECF是菱形．
老师说：“小凯的作法正确”．
回答下列问题：
根据小凯的做法，小明将题目改编为一道证明题，请你帮助小明完成下列步骤：
（1）已知：在平行四边形ABCD中，点E、F分别在边BC、AD上， ．（补全已知条件）
求证：四边形AECF是菱形．
（2）证明：（写出证明过程）
五．解答题（共1小题，满分10分，每小题10分）
22．如图，直线y＝2x+6与反比例函数y＝（x＞0）的图象交于点A（1，m），与x轴交于点B，与y轴交于点D．
（1）求m的值和反比例函数的表达式；
（2）观察图象，直接写出不等式2x+6﹣＞0的解集；
（3）在反比例函数图象的第一象限上有一动点M，当S△BDM＞S△BOD时，直接写出点M纵坐标的的取值范围．
六．解答题（共1小题，满分10分，每小题10分）
23．如图，BD是平行四边形ABCD的对角线，DE⊥AB于点E，过点E的直线交BC于点G，且BG＝CG．
（1）求证：GD＝EG．
（2）若BD⊥EG垂足为O，BO＝2，DO＝4，画出图形并求出四边形ABCD的面积．
（3）在（2）的条件下，以O为旋转中心顺时针旋转△GDO，得到△G′D'O，点G′落在BC上时，请直接写出G′E的长．
七．解答题（共1小题，满分12分，每小题12分）
24．如图1，在矩形ABCD中，AB＝1，对角线AC，BD相交于点O，∠COD＝60°，点E是线段CD上一点，连接OE，将线段OE绕点O逆时针旋转60°得到线段OF，连接DF．
（1）求证：DF＝CE；
（2）连接EF交OD于点P，求DP的最大值；
（3）如图2，点E在射线CD上运动，连接AF，在点E的运动过程中，若AF＝AB，求OF的长．
八．解答题（共1小题，满分12分，每小题12分）
25．如图，抛物线y＝ax2+bx（a≠0）与x轴交于原点及点A，且经过点B（4，8），对称轴为直线x＝﹣2，顶点为D．
（1）填空：抛物线的解析式为 ，顶点D的坐标为 ，直线AB的解析式为 ；
（2）在直线AB左侧抛物线上存在点E，使得∠EBA＝∠ABD，求E的坐标；
（3）连接OB，点P为x轴下方抛物线上一动点，过点P作OB的平行线交直线AB于点Q，当S△POQ：S△BOQ＝1：2时，求出点P的坐标．
参考答案与试题解析
一．选择题（共10小题，满分20分，每小题2分）
1．解：∵线段c是a、b的比例中项，
∴c2＝ab＝1×2，
解得c＝±，
又∵线段是正数，
∴c＝．
故选：B．
2．解：A、y＝2（x﹣1）2﹣8，
∵a＝2＞0，
∴图象的开口向上，故本选项错误；
B、当x＞1时，y随x的增大而增大；故本选项错误；
C、当x＜1时，y随x的增大而减小，故本选项正确；
D、图象的对称轴是直线x＝1，故本选项错误．
故选：C．
3．解：该几何体的俯视图是：由两个长方形组成的矩形，且矩形的之间有纵向的线段隔开．
故选：B．
4．解：依题意，得：150（1+a%）2＝216．
故选：C．
5．解：矩形木框在地面上形成的投影应是平行四边形或一条线段，
即相对的边平行或重合，
故D不可能，即不会是梯形．
故选：D．
6．解：二次函数y＝（x﹣1）2+2的图象的顶点坐标为（1，2），
∴向右平移1个单位长度后的函数图象的顶点坐标为（2，2），
∴所得的图象解析式为y＝（x﹣2）2+2．
故选：C．
7．解：设第一件商品x元，买两件商品共打了y折，根据题意可得：
x+0.5x＝2x•，
解得：y＝7.5
即相当于这两件商品共打了7.5折．
故选：D．
8．解：由图可得，
a＜0，c＞0，
∴正比例函数y＝ax的图象经过第二、四象限，且经过原点，
反比例函数y＝的图象在第一、三象限，
故选：C．
9．解：由表可以看出，当x取1.1与1.2之间的某个数时，y＝0，即这个数是x2+12x﹣15＝0的一个根．
x2+12x﹣15＝0的一个解x的取值范围为1.1＜x＜1.2．
故选：A．
10．解：∵△ABC和△EDC是以点C为位似中心的位似图形，
而△ABC和△EDC的周长之比为1：2，
∴△ABC和△EDC的位似比为1：2，
把C点向右平移2个单位到原点，则A点向右平移2个单位的对应点的坐标为（﹣2，3），
点（﹣2，3）以原点为位似中心的对应点的坐标为（4，﹣6），
把点（4，﹣6）向左平移2个单位得到（2，﹣6），
∴E点坐标为（2，﹣6）．
故选：C．
二．填空题（共6小题，满分18分，每小题3分）
11．解：设手臂竖直举起时总高度xm，列方程得：＝，
解得x＝2.34，
2.34﹣1.8＝0.54m，
所以小明举起的手臂超出头顶的高度为0.54m．
故答案为：0.54．
12．解：∵关于x的一元二次方程x2﹣x﹣1＝0有两个不相等的实数根，
∴△＝（﹣）2﹣4×1×（﹣1）＞0且k﹣2≥0，
解得：k≥2．
故答案为：k≥2．
13．解：∵矩形CDFE∽矩形ADCB，
∴＝，即＝，
整理得，AD2﹣2AD﹣4＝0，
解得，AD1＝1﹣（舍去），AD2＝1+，
故答案为：1+．
14．解：如图，设AC与A′B′相交于点D，
根据平移的性质，AB∥A′B′，
∴△DB′C∽△ABC，
∵重叠部分（图中阴影部分）的面积是△ABC的，
∴（）2＝，
∵BC＝，
∴B′C＝1，
∴BB′＝BC﹣B′C＝﹣1．
故答案为：﹣1．
15．解：设矩形花园BC的长为x米，则其宽为（54﹣x+2）米，依题意列方程得：
（54﹣x+2）x＝320，
x2﹣56x+640＝0，
解这个方程得：x1＝16，x2＝40，
∵28＜40，
∴x2＝40（不合题意，舍去），
∴x＝16，
∴AB＝（54﹣x+2）＝20．
答：当矩形的长AB为16米时，矩形花园的面积为320平方米；
故答案为：20．
16．解：如图所示：
∵EF⊥AE，
∴∠AEF＝90°，
又∵∠AED+∠AEF+∠CEF＝180°，
∴∠AED+∠CEF＝90°，
又∵四边形ABCD是矩形，
∴∠D＝∠C＝90°，
又∵∠AED+∠DAE＝90°，
∴∠DAE＝∠CEF，
∴△ADE∽△ECF，
∴，
又∵AB＝4，AD＝6，AB＝EC+ED，
∴，
解得：CF＝＝，
又∵0≤CE≤4，
∴，
故答案为．
三．解答题（共3小题，满分22分）
17．解：x2+4x﹣5＝0，
∵a＝1，b＝4，c＝﹣5，
∴△＝b2﹣4ac＝42﹣4×1×（﹣5）＝36，
则x＝＝，
解得x1＝﹣5，x2＝1．
18．解：（﹣2）﹣2﹣|﹣2|+（﹣）0﹣﹣2cs30°
＝﹣2++1﹣2﹣2×
＝﹣2．
19．解：（1）∵在2个收费通道A，B中，可随机选择其中的一个通过．
∴一辆汽车经过此收费站时，选择A通道通过的概率＝，
故答案为：；
（2）画树状图得：
∵共有8种等可能的情况，其中至少有两辆汽车选择B通道通过的有4种情况，
∴至少有两辆汽车选择B通道通过的概率为＝．
四．解答题（共2小题，满分16分，每小题8分）
20．解：∵AC＝，AD＝2，
∴CD＝＝．要使这两个直角三角形相似，有两种情况：
（1）当Rt△ABC∽Rt△ACD时，有＝，∴AB＝＝3；
（2）当Rt△ACB∽Rt△CDA时，有＝，∴AB＝＝3．
故当AB的长为3或3时，这两个直角三角形相似．
21．（1）已知：在平行四边形ABCD中，点E、F分别在边BC、AD上，EF垂直平分AC；
求证：四边形AECF是菱形．
（2）证明：∵EF垂直平分AC，
∴EA＝EC，FA＝FC，AC⊥EF，
∵四边形ABCD为平行四边形，
∴AD∥BC，
∴∠DAC＝∠ECA，
∵EA＝EC，
∴∠ECA＝∠EAC，
∴∠EAC＝∠DAC，
∴AC平分EF，
即AC与EF互相垂直平分，
∴四边形AECF是菱形．
故答案为 EF垂直平分AC．
五．解答题（共1小题，满分10分，每小题10分）
22．解：（1）∵直线y＝2x+6过点A（1，m），
∴m＝2×1+6＝8，
∴点A的坐标为（1，8），
∵点A（1，8）在反比例函数y＝（x＞0）的图象上，
∴k＝1×8＝8，
∴反比例函数的解析式为y＝；
（2）在A点右边，即x＞1时，直线在双曲线上方，
所以不等式2x+6﹣＞0的解集是x＞1；
（3）如图，过点O作AB的平行线，交反比例函数的图象于点N，则S△BDN＝S△BOD．
∵直线AB的解析式为y＝2x+6，
∴直线ON的解析式为y＝2x．
由（x＞0），解得，
∴点N的坐标为（2，4）；
∵S△BDM＞S△BOD，
∴S△BDM＞S△BDN，
∴M在N的右边，
∴0＜点M纵坐标＜4．
六．解答题（共1小题，满分10分，每小题10分）
23．证明：（1）如图1，延长EG交DC的延长线于点H，
∵四边形ABCD是平行四边形，
∴AD＝BC，AD∥BC，AB＝CD，AB∥CD，
∵AB∥CD，
∴∠H＝GEB，且BG＝CG，∠BGE＝∠CGH，
∴△CGH≌△BGE（AAS）
∴GE＝GH，
∵DE⊥AB，DC∥AB，
∴DC⊥DE，且GE＝GH，
∴DG＝EG＝GH；
（2）如图1：∵DB⊥EG，
∴∠DOE＝∠DEB＝90°，且∠EDB＝∠EDO，
∴△DEO∽△DBO，
∴
∴DE×DE＝4×（2+4）＝24，
∴DE＝2，
∴EO＝＝＝2，
∵AB∥CD，
∴，
∴HO＝2EO＝4，
∴EH＝6，且EG＝GH，
∴EG＝3，GO＝EG﹣EO＝，
∴GB＝＝＝，
∴BC＝2＝AD，
∴AD＝DE，
∴点E与点A重合，
如图2：
∵S四边形ABCD＝2S△ABD，
∴S四边形ABCD＝2××BD×AO＝6×2＝12；
（3）如图3，过点O作OF⊥BC，
∵旋转△GDO，得到△G′D'O，
∴OG＝OG'，且OF⊥BC，
∴GF＝G'F，
∵OF∥AB，
∴＝＝，
∴GF＝BG＝，
∴GG'＝2GF＝，
∴BG'＝BG﹣GG'＝，
∵AB2＝AO2+BO2＝12，
∵EG'＝AG'＝＝，＝．
七．解答题（共1小题，满分12分，每小题12分）
24．（1）证明：由题意知∠FOE＝∠DOC＝60°，
∴∠FOE﹣∠DOC﹣∠DOE，
即∠FOD＝∠EOC，
在矩形ABCD中，AC＝BD＝2OC＝2OD，
∴OC＝OD，
又∵OF＝OE，
∴△FOD≌△EOC（SAS），
∴DF＝CE；
（2）解：在△ODC中，OD＝OC，∠COD＝60°，
∴△OCD是等边三角形，∠OCD＝60°，
又△FOD≌△EOC，
∴∠FDO＝∠ECO＝60°，
在△OEF中，OE＝OF，∠EOF＝60°，
∴△OEF是等边三角形，∠OEF＝60°，
∴180°﹣∠FDP﹣∠FPD＝180°﹣∠OEP﹣∠OPE，
即∠DEP＝∠DOE，
又∠FDP＝∠ODE＝60°，
∴△FDP∽△ODE，
∴，
设DF＝CE＝x，则DE＝1﹣x，
∴，
∴DP＝﹣x2+x＝，
∴DP的最大值为．
（3）解：①在矩形ABCD中，AB＝1，∠COD＝60°，
∴AD＝，∠OAD＝∠ODA＝30°，
∴∠FDA＝∠FDO﹣∠ODA＝30°，
如图1，过点F作FM⊥AD于点M，
设FM＝m，则MD＝m，AM＝m，
又∵AF＝AB＝1，
∴在Rt△AFM中，AM2+FM2＝AF2，
∴＝1，
∴m1＝，m2＝1（舍去），
∴sin∠FAM＝，
∴∠FAM＝30°，
∴∠FAO＝60°，且AF＝AB＝AO，
∴△AOF是等边三角形，
∴OF＝1．
②如图2，过点A作AN⊥DF于点N，则∠FDA＝30°，
∴∠DAN＝60°，AN＝，
∴cs∠FAN＝，
∴∠FAN＝30°，
∴∠FAO＝120°，
又∠AOD＝120°，
∴∠FAO＝∠AOD，
又AF＝AO＝OD，
∴△OAF≌△AOD（SAS），
∴OF＝AD＝．
综合以上可得，OF＝1或．
八．解答题（共1小题，满分12分，每小题12分）
25．解：（1）对称轴为直线x＝﹣2，则点A（﹣4，0），
将点A、B的坐标代入抛物线表达式并解得：a＝，b＝1，
故抛物线的表达式为：y＝x2+x…①，
顶点D的坐标为：（﹣2，﹣1），
将点A、B的坐标代入一次函数表达式并解得：
直线AB的表达式为：y＝x+4…②，
故答案为：y＝x2+x；（﹣2，﹣1）；y＝x+4；
（2）作点D关于AB的对称点D′，分别过点D、D′作x轴的平行线交直线AB与点G、H，
则四边形GDHD′为正方形，点D（﹣2，﹣1），则点G（﹣5，﹣1），则正方形的边长为3，
则点D′（﹣5，2），
将B、D′的坐标代入一次函数表达式并解得：
直线BD′的表达式为：y＝x+…③；
联立①③并解得：x＝﹣或4（舍去），
故点P（﹣，）；
（3）取OB的中点H（2，4），则S△OQH＝S△OBQ，而S△POQ：S△BOQ＝1：2，
故S△OQH＝S△POQ，
∵PQ∥OH，故PQ＝OH（四边形PQHO为平行四边形），
则xQ﹣xP＝xH﹣xO，
设点P（m， m2+m），
直线OB的表达式为：y＝2x，
则直线PQ的表达式为：y＝2x+b，将点P的坐标代入上式并解得：
直线PQ的表达式为：y＝2x+m2﹣m…④，
联立②④并解得：xQ＝﹣m2+m+4，
而xQ﹣xP＝xH﹣xO，
即﹣m2+m+4﹣m＝2，
解得：m＝（舍去正值），
故点P（﹣2，2﹣2）．
x
1.1
1.2
1.3
1.4
1.5
x2+12x﹣15
﹣0.59
0.84
2.29
3.76
5.25