



高中数学人教版新课标A必修13.1.1方程的根与函数的零点课前预习课件ppt
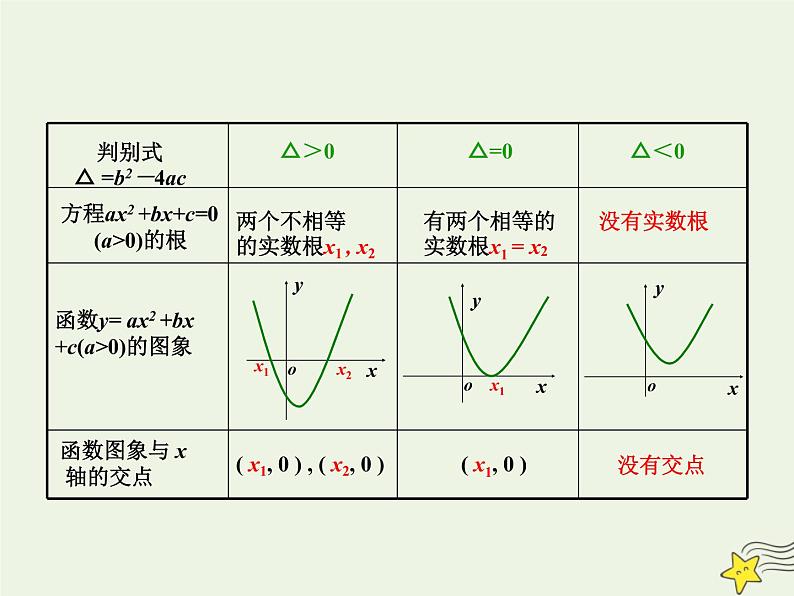
展开求下列方程的实数根,画出相应函数的简图,并求出函数图象与x轴交点的坐标,完成表格.
方程ax2 +bx+c=0 (a>0)的根
函数y= ax2 +bx+c(a>0)的图象
判别式△ =b2-4ac
函数图象与 x 轴的交点
有两个相等的实数根x1 = x2
( x1, 0 ) , ( x2, 0 )
两个不相等的实数根x1 , x2
对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点.
方程 f(x)=0 有实数根
函数的图象与x轴有交点
函数零点的求法:(1)代数法:求方程f(x)=0的根; (2)几何法:利用函数的图象求解.
例1 判断下列函数是否有零点,若存在请 求出零点.
若函数y=f(x), x∈[a,b],在开区间(a,b)内一定存在零点,应满足什么条件?
(1) f(a)f(b)>0
(2) f(a)f(b)<0
(3) f(a)f(b)=0
如果函数y=f(x)在区间[a,b]上的图象是 连续不断的一条曲线,并且有f(a)·f(b)<0, 那么,函数y=f(x)在区间(a,b) 内有零点.
即存在 c∈(a,b) ,使得 f(c) =0,这个c也就是方程 f(x)=0 的根.
高中数学人教版新课标A必修13.2.1几类不同增长的函数模型教学演示ppt课件: 这是一份高中数学人教版新课标A必修13.2.1几类不同增长的函数模型教学演示ppt课件,共27页。PPT课件主要包含了y=axa>1,y=xnn>0,答案B,题型一增长率模型,题型三分段函数模型等内容,欢迎下载使用。
数学人教版新课标A3.1.1方程的根与函数的零点背景图ppt课件: 这是一份数学人教版新课标A3.1.1方程的根与函数的零点背景图ppt课件,共47页。PPT课件主要包含了fx0,[ab],c∈ab等内容,欢迎下载使用。
2020-2021学年3.1.1方程的根与函数的零点说课ppt课件: 这是一份2020-2021学年3.1.1方程的根与函数的零点说课ppt课件,共46页。PPT课件主要包含了fx=0,横坐标,实数根,连续不断等内容,欢迎下载使用。













