人教版新课标A2.1.2指数函数及其性质教案

这是一份人教版新课标A2.1.2指数函数及其性质教案，共8页。
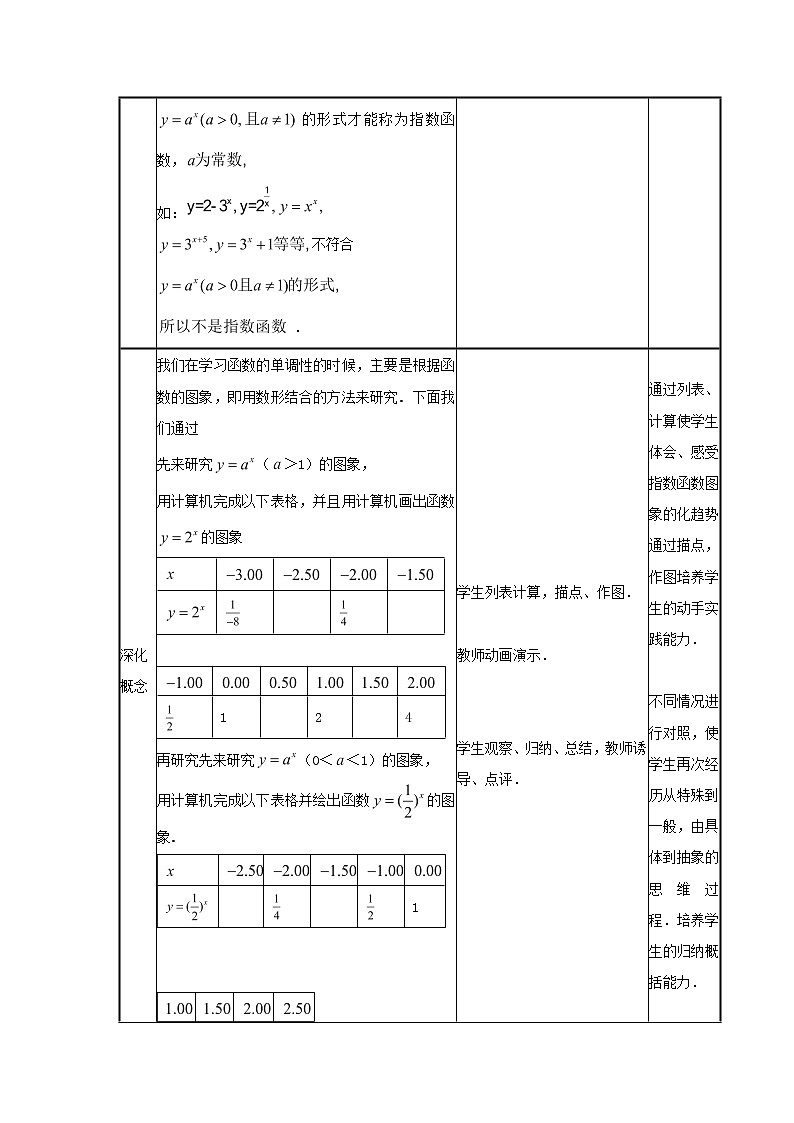
指数函数及其性质（一）（一）教学目标1．知识与技能了解指数函数模型的实际背景，理解指数函数的概念，掌握指数函数的图象．2．过程与方法能借助计算器或计算机画出具体指数函数的图象，探索指数函数图象特征．3．情感、态度与价值观在解决简单实际问题的过程中，体会指数函数是一类重要的函数模型，激发学生学习数学的兴趣，努力培养学生的创新意识．（二）教学重点、难点1．教学重点：指数函数的概念和图象．2．教学难点：指数函数的概念和图象．（三）教学方法采用观察、分析、归纳、抽象、概括，自主探究，合作交流的教学方法，通过各种教学媒体（如计算机或计算器），调动学生参与课堂教学的主动性和积极性．（四）教学过程教学环节教学内容师生互动设计意图复习引入1. 在本章的开头，问题（1）中时间与GDP值中的，请问这两个函数有什么共同特征.    2. 这两个函数有什么共同特征，从而得出这两个关系式中的底数是一个正数，自变量为指数，即都可以用（＞0且≠1来表示）.学生思考回答函数的特征．由实际问题引入，不仅能激发学生的学习兴趣，而且可以培养学生解决实际问题的能力．形成概念              理解概念 指数函数的定义一般地，函数（＞0且≠1）叫做指数函数，其中是自变量，函数的定义域为R.回答：在下列的关系式中，哪些不是指数函数，为什么？（1）       （2）        （3）（4）        （5）           （6）（7）        （8）  （＞1，且）小结：根据指数函数的定义来判断说明：因为＞0，是任意一个实数时，是一个确定的实数，所以函数的定义域为实数集R.若＜0，如在实数范围内的函数值不存在.若=1, 是一个常量，没有研究的意义，只有满足的形式才能称为指数函数， 如：不符合 .学生独立思考，交流讨论，教师巡视，并注意个别指导， 学生探讨分析，教师点拨指导．由特殊到一般，培养学生的观察、归纳、概括的能力．    使学生进一步理解指数函数的概念.深化概念 我们在学习函数的单调性的时候，主要是根据函数的图象，即用数形结合的方法来研究. 下面我们通过先来研究（＞1）的图象，用计算机完成以下表格，并且用计算机画出函数的图象   1 2 4再研究先来研究（0＜＜1）的图象，用计算机完成以下表格并绘出函数的图象.  1   2 4     从图中我们看出通过图象看出实质是上的讨论：的图象关于轴对称，所以这两个函数是偶函数，对吗？②利用电脑软件画出的函数图象.问题：从画出的图象中，你能发现函数的图象与底数间有什么样的规律.从图上看（＞1）与两函数图象的特征——关于轴对称. 学生列表计算，描点、作图． 教师动画演示．  学生观察、归纳、总结，教师诱导、点评．通过列表、计算使学生体会、感受指数函数图象的化趋势，通过描点，作图培养学生的动手实践能力． 不同情况进行对照，使学生再次经历从特殊到一般，由具体到抽象的思维过程．培养学生的归纳概括能力．应用举例例1：（P66 例6）已知指数函数（＞0且≠1）的图象过点（3，π），求 学生思考、解答、交流，教师巡视，注意个别指导，发现带有普遍性的问题，应及时提到全体学生面前供大家讨论．例1分析：要求再把0，1，3分别代入，即可求得解：将点（3，π），代入得到，即，解得：，于是，所以，，.巩固所学知识，培养学生的数形结合思想和创新能力．归纳总结1、理解指数函数2、解题利用指数函数的图象，可有利于清晰地分析题目，培养数型结合与分类讨论的数学思想 . 学生先自回顾反思，教师点评完善．通过师生的合作总结，使学生对本节课所学知识的结构有一个明晰的认识，形成知识体系.课后作业作业：2.1 第四课时  习案学生独立完成巩固新知提升能力备选例题例1 指出下列函数哪些是指数函数：（1）；   （2）；（3）； （4）；（5）；  （6）；（7）；   （8）且.【分析】 根据指数函数定义进行判断.【解析】 （1）、（5）、（8）为指数函数；（2）是幂函数（后面2.3节中将会学习）；（3）是与指数函数的乘积；（4）底数，不是指数函数；（6）指数不是自变量，而底数是的函数；（7）底数不是常数.它们都不符合指数函数的定义.【小结】准确理解指数函数的定义是解好本问题的关键.例2 用计算机作出的图像，并在同一坐标系下作出下列函数的图象，并指出它们与指数函数y=的图象的关系，⑴y=与y=.          ⑵y=与y=.解：⑴作出图像，显示出函数数据表x-3-2-101230.1250.250.512480.250.51248160.512481632比较函数y=、y=与y=的关系：将指数函数y=的图象向左平行移动1个单位长度，就得到函数y=的图象，将指数函数y=的图象向左平行移动2个单位长度，就得到函数y=的图象⑵作出图像，显示出函数数据表x-3-2-101230.1250.250.512480.6250.1250.250.51240.31250.6250.1250.250.512比较函数y=、y=与y=的关系：将指数函数y=的图象向右平行移动1个单位长度，就得到函数y=的图象，将指数函数y=的图象向右平行移动2个单位长度，就得到函数y=的图象小结：⑴当m>0时，将指数函数y=的图象向右平行移动m个单位长度，就得到函数y=的图象；当m>0时，将指数函数y=的图象向左平行移动m个单位长度，就得到函数y=的图象