






- 第1章集合与逻辑1.1第1课时集合与元素课件 课件 8 次下载
- 第1章集合与逻辑1.2子集和补集课件 课件 8 次下载
- 第1章集合与逻辑1.3集合的交与并课件 课件 9 次下载
- 第1章集合与逻辑2.1命题课件 课件 8 次下载
- 第1章集合与逻辑2.2充分条件和必要条件课件 课件 9 次下载
高中第1章 集合与逻辑1.1 集合课堂教学ppt课件
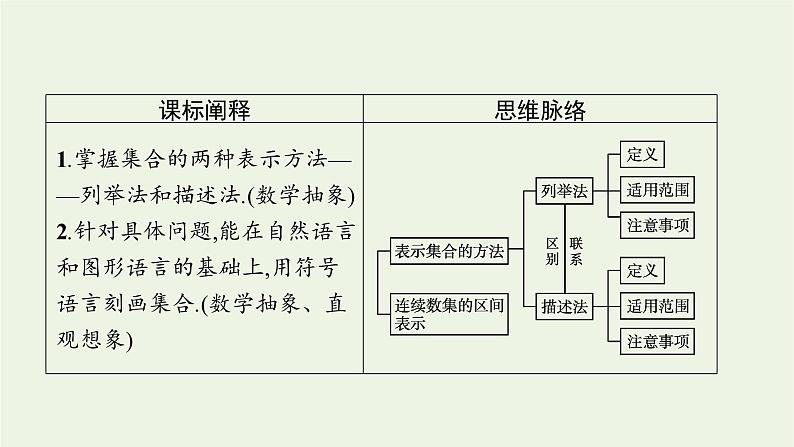
展开1.掌握集合的两种表示方法——列举法和描述法.(数学抽象)2.针对具体问题,能在自然语言和图形语言的基础上,用符号语言刻画集合.(数学抽象、直观想象)
根据集合的概念,我们知道:1.不等式2x+3<15的所有自然数解组成集合A;2.不等式2x+3<15的所有实数解组成集合B.同学们想一下,这两个集合有区别吗?如何表示这两个集合呢?
知识点一:列举法把集合中的元素一一列举出来.这叫作列举法.
名师点析 用列举法表示集合时,必须注意以下几点:(1)元素与元素之间需用“,”隔开.(2)不必考虑元素出现的前后顺序,但不能重复.(3)一般地,列举法适用于有限集:①元素个数有限且比较少时,可以全部列举出来,如{1,2,3};②元素个数有限且比较多时,可以列举一部分,中间用省略号表示,称为中间省略列举,如从1到1 000的所有正整数组成的集合,可以表示为{1,2,3,…,1 000}.
(4)对于含有较多元素的无限集,如果元素的排列呈现一定的规律,在不发生误解的情况下,也可列出几个元素作为代表,其他元素用省略号表示.如自然数集N可以表示为{0,1,2,3,…},称为尾端省略列举.(5)这里集合的“{ }”已包含“所有”的意思.例如{整数},即整数集Z,所以不能写成{全体整数}.
微练习(1)直线y=2x+1与y轴的交点所组成的集合为( )A.{0,1} B.{(0,1)}
(2)用列举法表示下列集合:①方程x2-9=0的解构成的集合;②不大于100的自然数构成的集合.解 ①{-3,3}.②{0,1,2,3,…,100}.
知识点二:描述法把集合中元素共有的,也只有该集合中元素才有的属性描述出来,以确定这个集合.这叫作描述法.
名师点析 使用描述法表示集合时要注意:(1)写清该集合中元素的代表符号,如{x|x>1}不能写成{x>1}.(2)用简明、准确的语言进行描述,如方程、不等式、几何图形等.(3)不能出现未被说明的字母,如{x∈Z|x=2m}中m未被说明,故此集合中的元素是不确定的.(4)元素的取值(或变化)范围,从上下文的关系来看,若x∈R是明确的,则x∈R可省略不写,如集合D={x∈R|x<20}也可表示为D={x|x<20}.
(5)多层描述时,应当准确使用“且”“或”等表示元素之间关系的词语,如{x|x<-1或x>1}.(6)“{ }”有“所有”“全体”的含义,如所有实数组成的集合可以用描述法表示为{x|x是实数},但如果写成{x|x是所有实数}、{x|x是全体实数}、{x|x是实数集}都是错误的,因为“{ }”本身既表示集合的意思,也表示了“所有”“全体”的意思.此处是初学者容易犯的错误,要注意领会.
微思考用列举法与描述法表示集合的区别是什么?
微练习不等式5x<2 018在实数范围内的解集可表示为 .
知识点三:区间的概念设a,b是两个实数,a
(1)如图,如何把满足数轴上的数的集合表示出来?(2)能否用更为简洁的符号表示A={x|-3
答案 (1){x|x<2}用区间表示为(-∞,2),用数轴表示如下:
(2){x|x≥3}用区间表示为[3,+∞),用数轴表示如下:
(3){x|-1≤x<5}用区间表示为[-1,5),用数轴表示如下:
例1用列举法表示下列集合:(1)36与60的公约数构成的集合;(2)方程(x-4)2(x-2)=0的根构成的集合;
分析(1)要明确公约数的含义;(2)注意4是重根;(3)要写成点集形式.
解 (1)36与60的公约数有1,2,3,4,6,12,所求集合可表示为{1,2,3,4,6,12}.(2)方程(x-4)2(x-2)=0的根是4,2,所求集合可表示为{2,4}.
反思感悟 列举法应用的解题策略(1)一般地,当集合中元素的个数较少时,可采用列举法;当集合中元素较多或无限,且有一定规律时,也可用列举法表示,但必须把元素间的规律呈现清楚,才能用省略号.(2)要弄清楚集合中的元素是什么,是数还是点,还是其他的元素,从而用相应的形式写出元素表示集合.
变式训练1试用列举法表示下列集合:(1)满足-3≤x≤0,且x∈Z;(2)倒数等于其本身数的集合;(3)满足x+y=3,且x∈N,y∈N的有序数对;(4)方程x2-4x+4=0的解.
解 (1)∵-3≤x≤0,且x∈Z,∴x=-3,-2,-1,0.故满足条件的集合为{-3,-2,-1,0}.(2)∵x= ,∴x=±1.∴满足条件的集合为{-1,1}.(3)∵x+y=3,且x∈N,y∈N,∴当x=0时,y=3;当x=1时,y=2;当x=2时,y=1;当x=3时,y=0.∴满足条件的集合为{(0,3),(1,2),(2,1),(3,0)}.(4)∵方程x2-4x+4=0的解为x=2,∴满足条件的集合为{2}.
例2用描述法表示以下集合:(1)所有不小于2,且不大于20的实数组成的集合;
(3)200以内的正奇数组成的集合;(4)方程x2-5x-6=0的解组成的集合.分析用描述法表示集合时,关键要先弄清元素的属性是什么,再给出其满足的性质,注意不要漏掉类似“x∈N”等条件.
解 (1)集合可表示为{x∈R|2≤x≤20}.
(3){x|x=2k+1,x<200,k∈N}.(4){x|x2-5x-6=0}.
反思感悟 用描述法表示集合时应注意的问题(1)写清楚该集合中的代表元素,即弄清代表元素是数、点还是其他形式;(2)准确说明集合中元素所满足的特征;(3)所有描述的内容都要写在集合符号内,并且不能出现未被说明的符号;(4)用于描述的语句力求简明、准确,多层描述时,应准确使用“且”“或”等表示描述语句之间的关系.
变式训练2给出下列说法:①在平面直角坐标平面内,第一、三象限内的点组成的集合为{(x,y)|xy>0};②所有奇数组成的集合为{x|x=2n+1};③集合{(x,y)|y=1-x}与{x|y=1-x}是同一集合.其中正确的有( )A.1个B.2个C.3个D.0个
例3若集合A={x|kx2-8x+16=0}只有一个元素,试求实数k的值,并用列举法表示集合A.分析明确集合A的含义→对k加以讨论→求出k的值→写出集合A
解 当k=0时,原方程变为-8x+16=0,x=2.此时集合A={2},满足题意.当k≠0时,要使关于x的一元二次方程kx2-8x+16=0有两个相等实根,只需Δ=64-64k=0,即k=1.此时方程的解为x1=x2=4,集合A={4},满足题意.综上所述,实数k的值为0或1.当k=0时,A={2};当k=1时,A={4}.
反思感悟 1.解答与描述法有关的问题时,明确集合中代表元素及其共同特征是解题的切入点及关键点.2.本题因kx2-8x+16=0是否为一元二次方程,而分为k=0和k≠0两种情况进行讨论,从而做到不重不漏.3.解集合与含有参数的方程的综合问题时,一般要求对方程中最高次项的系数的取值进行分类讨论,确定方程的根的情况,进而求得结果.需特别关注判别式在一元二次方程的实数根个数的讨论中的作用.
延伸探究(1)本例中,若集合A中含有2个元素,试求k的取值集合.(2)本例中,若集合A中至多有一个元素,试求k的取值集合.
解得k<1,且k≠0,即{k|k<1,且k≠0}.(2)当集合A中含有1个元素时,由例3知,k=0或k=1;
例4(1)若集合M是一个数集,且可应用区间(a,3a-1)表示,则实数a的取值范围用区间表示为 ;
(3)若区间(5,a)的长度是12,则实数a的值是 .
(3)由区间长度的定义可知a-5=12,即a=17.
变式训练3(1)若区间[2,a]的长度不超过5,则实数a的取值范围用区间表示为 ;
解析 (1)由题意可知a-2≤5,且a>2,所以2
典例 下列四个集合:①{x|y=x2+1};②{y|y=x2+1,x∈R};③{(x,y)|y=x2+1};④{y=x2+1}.(1)它们各自的含义是什么?(2)它们是不是相同的集合?分析在解答用描述法表示的集合的问题时,不能只关注条件中的关系式,而不注意“代表元素”的含义.元素是集合的基本组成部分.看到一个集合,先要关注元素是什么,再关注元素的基本属性.
解 (1)①{x|y=x2+1}中的代表元素是x(二次函数y=x2+1中的自变量),表示的是该函数自变量的取值范围.显然x∈R,该集合表示实数集R.②{y|y=x2+1}中的代表元素是y(二次函数y=x2+1中的因变量),表示的是该函数的函数值构成的集合.由图易知(图略),y≥1,该集合就是{y|y≥1}.③{(x,y)|y=x2+1}中的代表元素是(x,y),该集合可以理解为是满足y=x2+1的有序实数对(x,y)的集合,也可以认为是坐标平面内满足y=x2+1的点(x,y)构成的集合.④集合{y=x2+1}表示的是以方程y=x2+1(或函数解析式y=x2+1)为元素的集合.(2)由(1)知,集合①是实数集,集合②是不小于1的实数集,集合③是抛物线上的点构成的点集,集合④是单元素集.故它们是互不相同的集合.
方法点睛元素分析法是解决集合问题时常用的基本方法.本题的分析始终关注集合中代表元素及其满足的条件.集合①是后面要学到的函数定义域,集合②是函数的值域.
1.集合{x∈N+|2x-1<9}的另一种表示方法是( )A.{0,1,2,3,4}B.{1,2,3,4}C.{0,1,2,3,4,5}D.{1,2,3,4,5}答案 B
2.不等式x-2≥0的所有解组成的集合表示成区间是( )A.(2,+∞)B.[2,+∞)C.(-∞,2)D.(-∞,2]答案 B解析 不等式x-2≥0的所有解组成的集合为{x|x≥2},表示成区间为[2,+∞).
3.(2021山东临沂高一期中)已知b是正数,且集合{x|x2-ax+16=0,a∈R}={b},则a-b=( )A.0B.2C.4D.8答案 C解析 由题意可知方程x2-ax+16=0有两个相等的正实根,故Δ=a2-64=0.又方程两根之和为正数,即a>0,所以a=8.因此方程为x2-8x+16=0,且根为4,故b=4,所以a-b=8-4=4.故选C.
4.若A={2,3,4},B={x|x=n-m,m,n∈A,m≠n},则集合B中的元素个数为 . 答案 4解析 当n=2,m=3时,n-m=-1;当n=2,m=4时,n-m=-2;当n=3,m=4时,n-m=-1;当n=3,m=2时,n-m=1;当n=4,m=2时,n-m=2;当n=4,m=3时,n-m=1.所以集合B中的元素共4个:-2,-1,1,2.
数学必修 第一册第一章 集合与常用逻辑用语1.1 集合的概念图文ppt课件: 这是一份数学必修 第一册第一章 集合与常用逻辑用语1.1 集合的概念图文ppt课件,共33页。
高中数学上教版(2020)必修 第一册1.1 集合初步精品ppt课件: 这是一份高中数学上教版(2020)必修 第一册1.1 集合初步精品ppt课件,共29页。PPT课件主要包含了闭区间,开区间等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第一册第一章 集合与常用逻辑用语1.1 集合的概念集体备课ppt课件: 这是一份高中数学人教A版 (2019)必修 第一册第一章 集合与常用逻辑用语1.1 集合的概念集体备课ppt课件,共36页。PPT课件主要包含了内容索引,课前篇自主预习,课堂篇探究学习,课标阐释,思维脉络,知识点拨等内容,欢迎下载使用。













