




高中数学5.5 三角函数模型的简单应用评课ppt课件
展开1.能根据y=Asin(ωx+φ)的部分图象,确定其解析式.(直观想象)2.会用三角函数解决简单的实际问题.(数学运算)3.可以利用三角函数构建刻画事物周期变化的数学模型.(数学建模)
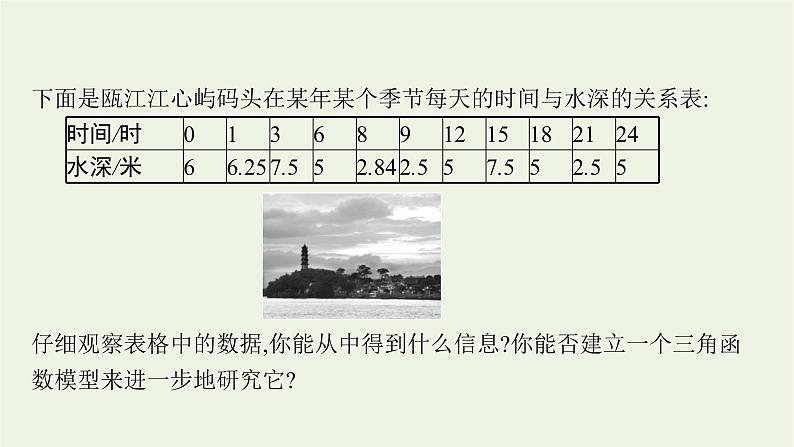
江心屿,位于浙江省温州市区北面瓯江中游,属于中国四大名屿.该屿风景秀丽,东西双塔凌空,映衬江心寺,历来被称为“瓯江蓬莱”.江心寺为全国32所观音道场之一,分前、中、后三殿,殿内槛联匾额,琳琅满目.寺院大门两边有一著名的叠字联:“云朝朝,朝朝朝,朝朝朝散;潮长长,长长长,长长长消(念‘yúnzhāchá,zhāzhāchá,zhācházhāsàn;cháchángzhǎng,chángchángzhǎng,chángzhǎngchángxiā’).”该对联巧妙地运用了叠字诗展现了瓯江潮水涨落的壮阔画面.
下面是瓯江江心屿码头在某年某个季节每天的时间与水深的关系表:
仔细观察表格中的数据,你能从中得到什么信息?你能否建立一个三角函数模型来进一步地研究它?
知识点:应用三角函数模型解决问题的一般程序应用三角函数模型解决问题,首先要把实际问题抽象为数学问题,通过分析它的变化趋势,确定它的周期,从而建立起适当的三角函数模型,解决问题的一般程序如下:(1)审题,先审清楚题目条件、要求、理解数学关系.(2)建模,分析题目特性,选择适当的三角函数模型.(3)求解,对所建立的三角函数模型进行分析研究得到数学结论.
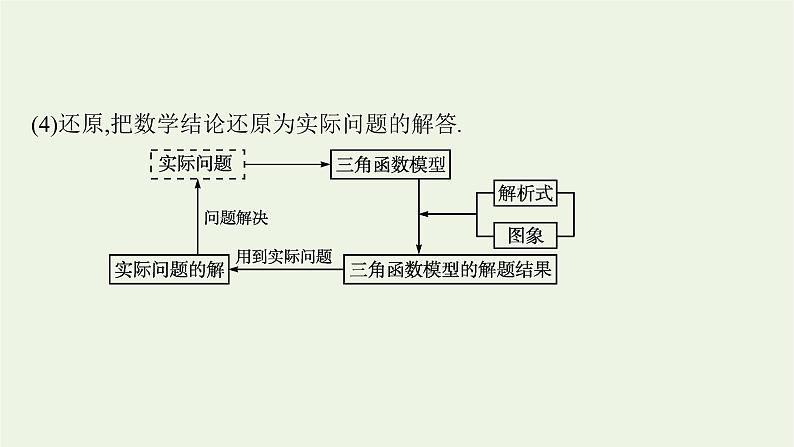
(4)还原,把数学结论还原为实际问题的解答.
微练习如图是相对于平均海平面的某海湾的水面高度h(单位:米)在某天从0~24时的变化情况,则水面高度h关于时间t的函数关系式为 .
反思感悟 给出y=Asin(ωx+φ)的图象的一部分,确定A,ω,φ的方法(1)逐一定参法:先通过图象确定A和ω,再选取“第一零点”(即“五点法”作图中的第一个点)的数据代入“ωx+φ=0”(要注意正确判断哪一点是“第一零点”),求得φ的值.(2)待定系数法:通过若干特殊点代入函数式,可以求得相关待定系数A,ω,φ.但需要注意的是,要认清所选择的点属于五个点中的哪一点,并能正确代入解析式.(3)图象变换法:运用逆向思维的方法,先确定函数的基本解析式y=Asin ωx,再根据图象平移规律确定相关的参数.
变式训练1已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的部分图象如图所示,则函数f(x)的解析式为( )
例2已知电流I与时间t的关系为I=Asin(ωt+φ).
(1)如图所示的是I=Asin(ωt+φ) (A>0,ω>0,|φ|< )在一个周期内的图象,根据图中数据求I=Asin(ωt+φ)的解析式;(2)如果t在任意一段 秒的时间内,电流I=Asin(ωt+φ)(ω>0)都能取得最大值和最小值,那么ω的最小正整数值是多少?
∴ω≥300π>942,又ω∈N+,∴ω的最小正整数值是943.
反思感悟 例题中的函数模型已经给出,观察图象和利用待定系数法可以求出解析式中的未知参数,从而确定函数解析式.此类问题解题关键是将图形语言转化为符号语言,其中,读图、识图、用图是数形结合的有效途径.
变式训练2心脏跳动时,血压在增加或减少.血压的最大值、最小值分别称为收缩压和舒张压,血压计上的读数就是收缩压和舒张压,读数120/80 mmHg为标准值.设某人的血压满足函数式p(t)=115+25sin 160πt,其中p(t)为血压(单位:mmHg),t为时间(单位:min),试回答下列问题:(1)求函数p(t)的周期;(2)求此人每分钟心跳的次数;(3)求出此人的血压在血压计上的读数.
例3已知某海滨浴场的海浪高度y(单位:米)是时间t(单位:时)的函数,其中0≤t≤24,记y=f(t),下表是某日各时的浪高数据:
经长期观测,y=f(t)的图象可近似地看成是函数y=Acs ωt+b的图象.(1)根据以上数据,求其最小正周期、振幅及函数解析式;(2)根据规定,当海浪高度大于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的8:00到20:00之间,有多少时间可供冲浪者进行活动?
又0≤t≤24,所以0≤t<3或9
又0≤t≤24,所以0≤t<2或10
直观想象核心素养在研究与三角函数有关的零点问题中的应用
典例(2021甘肃天水一中高一期中)如图是函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|≤ )的部分图象.(1)求函数f(x)的表达式;(2)若函数f(x)满足方程f(x)=a(0
由f(x)-a=0得f(x)=a,
1.若函数y=sin(ωx+φ)(ω>0)的部分图象如图,则ω=( )A.5B.4C.3D.2
2.如图是一向右传播的绳波在某一时刻绳子各点的位置图,经过 周期后,乙的位置将移至( )A.x轴上B.最低点C.最高点D.不确定
答案 C解析 相邻的最大值与最小值之间间隔半个周期,故乙移至最高点.
3.函数y=sin(ωx+φ)(x∈R,ω>0,0≤φ<2π)的部分图象如图所示,则( )
5.如图为函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象的一段.(1)求其解析式;(2)若将y=Asin(ωx+φ)的图象向左平移 个单位长度后得到函数y=f(x)的图象,求函数y=f(x)图象的对称轴.
高中数学湘教版(2019)必修 第一册5.5 三角函数模型的简单应用获奖课件ppt: 这是一份高中数学湘教版(2019)必修 第一册5.5 三角函数模型的简单应用获奖课件ppt,文件包含55三角函数模型的简单应用doc、55三角函数模型的简单应用pptx等2份课件配套教学资源,其中PPT共0页, 欢迎下载使用。
高考数学(理)一轮复习课件+讲义 第4章 第5讲 函数y=Asin(ωx+φ)的图象及三角函数模型的简单应用: 这是一份高考数学(理)一轮复习课件+讲义 第4章 第5讲 函数y=Asin(ωx+φ)的图象及三角函数模型的简单应用,文件包含高考数学理一轮复习课件第4章第5讲函数y=Asinωx+φ的图象及三角函数模型的简单应用pptx、高考数学理一轮复习讲义第4章第5讲函数y=Asinωx+φ的图象及三角函数模型的简单应用doc等2份课件配套教学资源,其中PPT共60页, 欢迎下载使用。
湘教版(2019)必修 第一册第5章 三角函数5.5 三角函数模型的简单应用优质课ppt课件: 这是一份湘教版(2019)必修 第一册第5章 三角函数5.5 三角函数模型的简单应用优质课ppt课件,共24页。PPT课件主要包含了学习目标,新知学习,常考题型,随堂小测,课堂小结等内容,欢迎下载使用。













