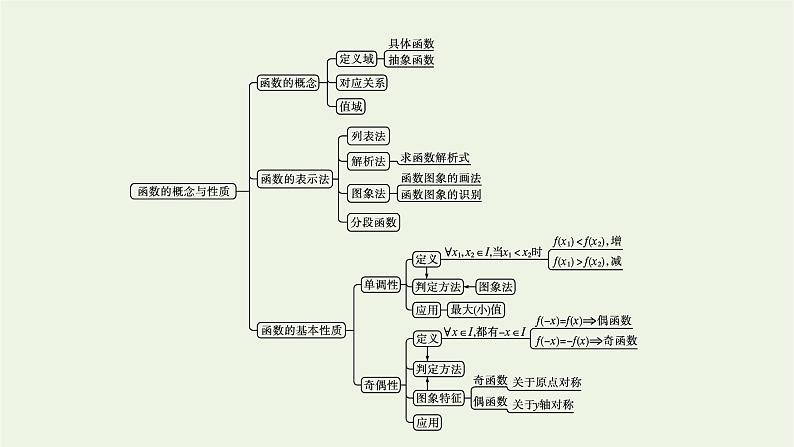
数学必修 第一册第3章 函数的概念与性质本章综合与测试精品课件ppt

这是一份数学必修 第一册第3章 函数的概念与性质本章综合与测试精品课件ppt，共36页。PPT课件主要包含了内容索引，知识网络整合构建，专题归纳思维深化，答案C，函数的单调性，答案D等内容，欢迎下载使用。

解析 方法1(代数法)根据题意求x的取值范围,需分四种情况讨论,具体如下:当1-x≥0,且x≥0,即0≤x≤1时,由f(1-x)>f(x),得(1-x)2>x2,
当1-x≥0,且x<0,即x<0时,由f(1-x)>f(x),得(1-x)2+1>1,解得x≠1,又x<0,所以x<0;当1-x<0,且x<0,此时x不存在,不满足要求;当1-x<0,且x≥0,即x>1时,由f(1-x)>f(x),得1>x2+1,此时不成立.
方法2(数形结合法)
方法技巧函数的图象与函数值间具有密切的关系,在函数图象上方的函数值大于下方所有函数图象对应的函数值,故可以根据函数图象的上、下位置关系,把不等式的解的问题转化为数量关系求解,如本例中借助分段函数的图象可以直接把求解的问题转化为1-x与x的关系求解.
(1)用定义证明函数f(x)在区间(-1,+∞)上的单调性;(2)求f(x)在区间[2,5]上的最大值和最小值.
方法技巧关于函数单调性的常见问题(1)利用单调性比较大小.(2)解抽象不等式.(3)求最值.关于函数单调性的应用一定注意x1,x2的取值在单调区间内.
A.(-∞,1)B.(1,+∞)C.(-∞,0)∪(0,1)D.(-∞,0)∪(1,+∞)
解析 由已知得 <1,解得x<0或x>1.故选D.
2.函数的奇偶性例3(2020安徽潜山校级期中)已知函数f(x)是R上的奇函数,当x≥0时,f(x)=2x2+x.(1)当x<0时,求f(x)的解析式;(2)若f(1-a)+f(2a+1)<0,求实数a的取值范围.
解 (1)根据题意,当x<0时,-x>0,则f(-x)=2(-x)2+(-x)=2x2-x.又由f(x)为奇函数,则f(x)=-f(-x)=-2x2+x,故当x<0时,f(x)=-2x2+x.(2)根据题意,当x≥0时,f(x)=2x2+x,函数y=2x2和y=x在区间[0,+∞)上都是增函数,则f(x)在[0,+∞)上为增函数.又由f(x)为奇函数,则f(x)在R上为增函数,f(1-a)+f(2a+1)<0⇒f(2a+1)<-f(1-a)⇒f(2a+1)方法技巧由函数奇偶性求函数解析式的解题策略(1)若f(x)是奇函数,且已知x>0时的解析式,则x<0时的解析式只需将原函数式y=f(x)中的x,y分别替换为-x,-y,然后解出y即可.(2)若f(x)是偶函数,且已知x>0时的解析式,则x<0时的解析式只需将原函数式y=f(x)中的x替换为-x,y不变,即得x<0时的解析式.
变式训练3(2020山西太原期中)已知y=f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2-2x.(1)求f(1),f(-2)的值;(2)求f(x)的解析式;(3)画出y=f(x)的简图,并写出y=f(x)的单调递增区间(只需写出结果,不要解答过程).
解 (1)当x≥0时,f(x)=x2-2x,f(-x)=f(x),∴f(1)=-1,f(-2)=f(2)=0.(2)∵y=f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2-2x,当x<0时,-x>0,f(-x)=(-x)2-2(-x)=x2+2x,∴f(x)=f(-x)=x2+2x.
∴当x≥0时,y=x2-2x,抛物线开口向上,对称轴为直线x=1,顶点坐标为(1,-1),当y=0时,x1=0,x2=2.当x<0时,y=x2+2x,抛物线开口向上,对称轴为直线x=-1,顶点坐标为(-1,-1),当y=0时,x=-2.由此能作出函数f(x)的图象如下:
结合图象知f(x)的单调递增区间是(-1,0),(1,+∞).
3.函数的奇偶性和单调性的应用
(1)确定f(x)的解析式;(2)用定义证明f(x)在区间(-2,2)上是减函数;(3)解不等式f(t-1)+f(t)<0.
方法技巧巧用奇偶性及单调性解不等式(1)利用已知条件,结合函数的奇偶性,把已知不等式转化为f(x1)f(x2)的形式.(2)根据奇函数在对称区间上的单调性一致,偶函数在对称区间上的单调性相反,脱掉不等式中的“f”,转化为简单不等式求解.
变式训练4(2021天津和平期末)已知定义在[-3,3]上的函数y=f(x)是增函数.(1)若f(m+1)>f(2m-1),求实数m的取值范围;(2)若函数f(x)是奇函数,且f(2)=1,解不等式f(x+1)+1>0.
(2)∵函数f(x)是奇函数,且f(2)=1,∴f(-2)=-f(2)=-1.∵f(x+1)+1>0,∴f(x+1)>-1,∴f(x+1)>f(-2),
例5已知函数f(x)=x2+2ax+2.(1)当a=-1时,求函数f(x)在区间[-5,5]上的最大值和最小值;(2)用a表示出函数f(x)在区间[-5,5]上的最值.分析将原函数先配方,对于第(2)题还要结合图象进行分类讨论.
解 (1)当a=-1时,f(x)=x2-2x+2=(x-1)2+1,因为1∈[-5,5],故当x=1时,f(x)取得最小值,f(x)min=f(1)=1;当x=-5时,f(x)取得最大值,f(x)max=f(-5)=(-5-1)2+1=37.(2)函数f(x)=x2+2ax+2=(x+a)2+2-a2的图象开口向上,对称轴为x=-a.当-a≤-5,即a≥5时,函数在区间[-5,5]上是增函数,所以f(x)max=f(5)=27+10a,f(x)min=f(-5)=27-10a;当-5<-a≤0,即0≤a<5时,函数图象如图①所示,由图象可得f(x)min=f(-a)=2-a2,f(x)max=f(5)=27+10a;当0<-a<5,即-5当-a≥5,即a≤-5时,函数在区间[-5,5]上是减函数,所以f(x)min=f(5)=27+10a,f(x)max=f(-5)=27-10a.综上可得,当a≥5时,f(x)在区间[-5,5]上的最大值为27+10a,最小值为27-10a;当0≤a<5时,f(x)在区间[-5,5]上的最大值为27+10a,最小值为2-a2;当-5方法技巧对于二次函数y=ax2+bx+c(a>0)的最值问题,首先应采用配方法,化为y=a(x-h)2+k的形式.(1)求二次函数在定义域R上的最值;(2)求二次函数在闭区间上的最值共有三种类型:①顶点固定,区间也固定.此种类型是较为简单的一种,只要找到对称轴,画出图象,将区间标出,最值一目了然.
②顶点变动,区间固定.这种类型是比较重要的,在高考题中多次出现,主要是讨论顶点横坐标即对称轴在区间左侧、在区间内部以及在区间右侧等情况,然后根据不同情况写出最值.③顶点固定,区间变动.此种情况用得较少,在区间里含有参数,根据区间分别在对称轴的左侧、包含对称轴以及在对称轴右侧进行讨论.