高中数学湘教版（2019）必修 第一册第2章 一元二次函数、方程和不等式本章综合与测试优质ppt课件

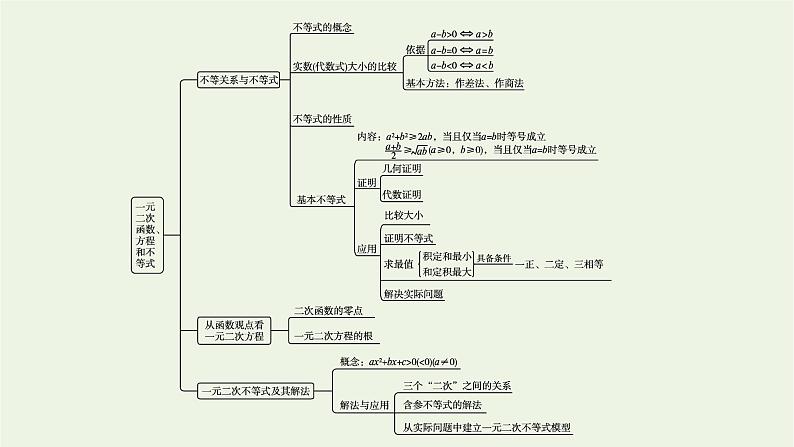
这是一份高中数学湘教版（2019）必修 第一册第2章 一元二次函数、方程和不等式本章综合与测试优质ppt课件，共23页。PPT课件主要包含了内容索引，知识网络整合构建，专题归纳思维深化，答案B等内容，欢迎下载使用。

例1已知x1,x2是一元二次方程4kx2-4kx+k+1=0的两个实数根.
方法技巧一元二次方程的根及其根与系数的关系,虽在高考中不直接考查,但它是解决某些数学问题的基础,常在解题过程中用到.
变式训练1已知关于x的一元二次方程kx2-(k-1)x-1=0.(1)求证:方程有两个实数根.(2)当k为何值时,此方程的两个实数根互为相反数?(3)我们定义:若一元二次方程ax2+bx+c=0的两个正实数根x1,x2(x1>x2),满足2< <3,则称这个一元二次方程有两个“梦想根”.如果关于x的一元二次方程 kx2-(k-1)x-1=0有两个“梦想根”,求k的取值范围.
(1)证明∵关于x的一元二次方程kx2-(k-1)x-1=0,a=k,b=-(k-1),c=-1,Δ=b2-4ac=[-(k-1)]2-4k×(-1)=k2+2k+1=(k+1)2≥0,∴关于x的一元二次方程kx2-(k-1)x-1=0有两个实数根.
(1)若m=1,求当x>1时函数的最小值;(2)当x<1时,函数有最大值-3,求实数m的值.分析(1)由函数的形式可以看出,求最小值可用基本不等式求解;(2)当x<1时,x-1<0,仍可用基本不等式求最值,利用等号成立的条件求参数m的值.
方法技巧 基本不等式是证明不等式、求某些函数的最大值及最小值的理论依据,在解决数学问题和实际问题中应用广泛.
例3已知关于x的不等式x2+mx>4x+m-4.(1)若对一切实数x不等式恒成立,求实数m的取值范围;(2)若对一切大于1的实数x不等式恒成立,求实数m的取值范围.分析(1)不等式为一元二次不等式,利用判别式小于0,即可求m的取值范围;(2)通过对一切大于1的实数x不等式恒成立,判断对应二次函数图象对称轴的位置及当x=1时y的值,即可求m的取值范围.
解 (1)将不等式x2+mx>4x+m-4整理,转化为x2+(m-4)x-m+4>0.由Δ=(m-4)2-4(4-m)<0,解得04x+m-4分离变量m,则原问题可等价于对一切
(方法2)令y=x2+(m-4)x-m+4.∵对一切大于1的实数x,y>0恒成立,
方法技巧 分离变量法解恒成立问题对于x在某取值范围内,y≥0(或y≤0)型恒成立问题,我们一般利用分离变量法转化为求解最大(小)值问题.而对于一元二次不等式问题,可以借助对应二次函数的图象与性质求解,注意要讨论对称轴与取值范围之间的关系,从而确定函数的最小(大)值.
变式训练3若关于x的不等式ax2-2x+2>0对于满足1

相关课件

高中数学湘教版（2019）必修 第一册第6章 统计学初步本章综合与测试完整版课件ppt：

这是一份高中数学湘教版（2019）必修 第一册第6章 统计学初步本章综合与测试完整版课件ppt，共20页。PPT课件主要包含了内容索引，知识网络整合构建，专题归纳思维深化，答案60等内容，欢迎下载使用。

湘教版（2019）第1章 集合与逻辑本章综合与测试精品课件ppt：

这是一份湘教版（2019）第1章 集合与逻辑本章综合与测试精品课件ppt，共24页。PPT课件主要包含了内容索引，知识网络整合构建，专题归纳思维深化等内容，欢迎下载使用。

高中数学4.1 一元二次函数备课ppt课件：

这是一份高中数学4.1 一元二次函数备课ppt课件，共28页。PPT课件主要包含了跟踪训练1，答案C，跟踪训练41等内容，欢迎下载使用。