2021学年15.3 分式方程教学课件ppt

这是一份精品课件2021学年15.3 分式方程教学课件ppt，共27页。PPT课件主要包含了情境问题，分式方程，解分式方程，分式方程解的检验，解分式方程的一般步骤，解分式方程的思路是，整式方程，一化二解三检验，练习解方程，增根的定义等内容，欢迎下载使用。
学习目标：　1．了解分式方程的概念．　2．会用去分母的方法解可化为一元一次方程的简单 的分式方程，体会化归思想和程序化思想．　3．了解解分式方程根需要进行检验的原因．学习重点： 利用去分母的方法解分式方程．
一艘轮船在静水中的最大航速为20千米/时,它沿江以最大航速顺流航行100千米所用时间,与以最大航速逆流航行60千米所用时间相等,江水的流速为多少?
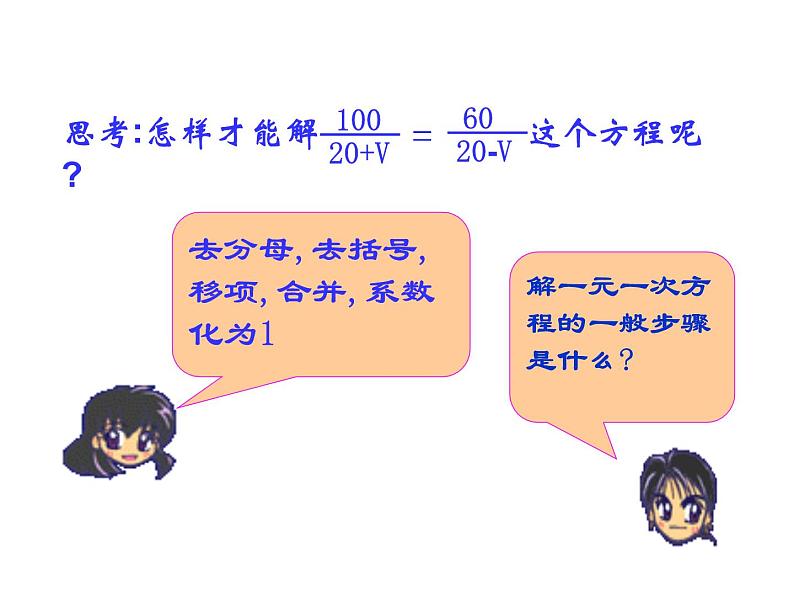
解:设江水的流速为 v 千米/时，根据题意，得
分母中含未知数的方程叫做分式方程.
像这样，分母里含有未知数的方程叫做分式方程。
以前学过的分母里不含有未知数的方程叫做整式方程。
分母中含未知数的方程叫做 分式方程.
整式方程的未知数不在分母中分式方程的分母中含有未知数
判断下列说法是否正确：
（是）[来源:z*x*x*k]
下列方程中，哪些是分式方程？哪些整式方程.
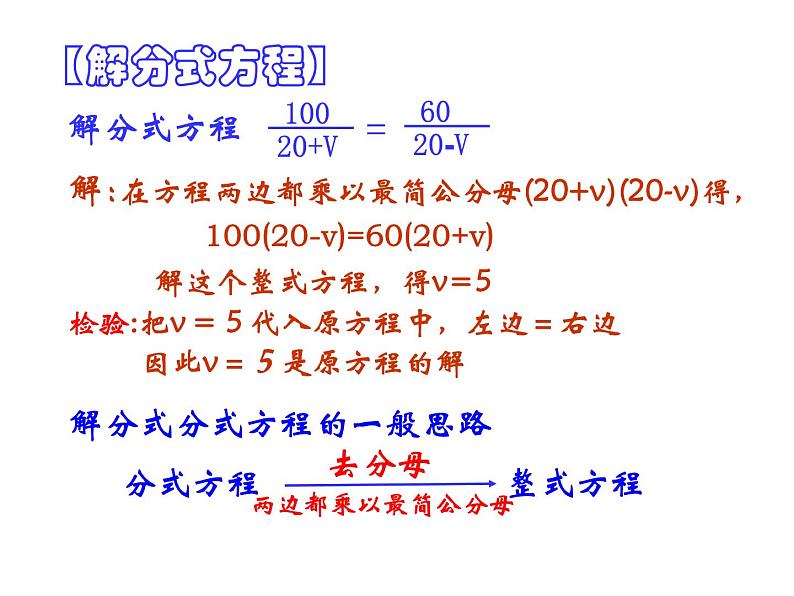
在方程两边都乘以最简公分母(20+v)(20-v)得，
解这个整式方程，得v=5
100(20-v)=60(20+v)
检验:把v = 5 代入原方程中，左边＝右边
因此v＝５是原方程的解
解分式分式方程的一般思路
分式方程中各分母的最简公分母是： (x+5)(x－5) 方程两边同乘 (x+5)(x－5) ，得： x+5=10 解得： x=5 检验：将x=5代入原方程中，分母x－5和x2－25的值 都为0，分式无意义. 所以，此分式方程无解.
两边同乘(20+v)(20-v)
当v=5时,(20+v)(20-v)≠0
两边同乘(x+5)(x-5)
当x=5时, (x+5)(x-5)=0
分式两边同乘了不为0的式子,所得整式方程的解与分式方程的解相同.
分式两边同乘了等于0的式子,所得整式方程的解使分母为0,这个整式方程的解就不是原分式方程的解
解分式方程时，去分母后所得整式方程的解有可能使原方程的分母为０，所以分式方程的解必须检验．
怎样检验这个整式方程的解是不是原分式的解？
将整式方程的解代入最简公分母，如果最简公分母的值不为０，则整式方程的解是原分式方程的解，否则这个解就不是原分式方程的解．
产生的原因:分式方程两边同乘一个零因式后,所得的根是整式方程的根,而不是分式方程的根.所以我们解完分式方程时一定要代入原分式方程或最简公分母进行检验.
为什么方程会产生无解？
1、 在方程的两边都乘以最简公分母，约去分母，化成整式方程. 2、解这个整式方程. 3、 把整式方程的解代入最简公分母，如果最简公分母的值不为0，则整式方程的解是原分式方程的解；否则，这个解不是原分式方程的解，必须舍去. 4、写出原方程的根.
解：方程两边同乘x(x－3) ，得： 2x=3x－9 解得： x=9 检验：将x=9时x(x－3) ≠0 因此 9是分式方程的解.
解：方程两边同乘 (x+2)(x－1) ，得： x (x+2)－(x+2)(x－1) =3 解得： x=1 检验：x=1时(x+2)(x－1) =0 ，1不是原分式方程的解，原分式方程无解.
2、x为何值时，代数式 的值等于2？
2.如果关于x的方程 无解,则m的值等于（ ）(A)-3 (B)-2 (C)-1 (D)3【解析】选B.方程的两边都乘(x-3),得2=x-3-m,移项并合并得,x=5+m，由于方程无解,此时x=3.即5+m=3,∴m=-2.
8. 关于x的方程 无解,求k的值.【解析】方程的两边同时乘(x+3)(x-3)得x+3+kx-3k=k+3整理得:(k+1)x=4k因为方程无解,则x=3或x=-3当x=3时,(k+1) ·3=4k,k=3,当x=-3时,(k+1)(-3)=4k, 所以当k=3或 时,原分式方程无解.
7. (德化·中考)如图,点A,B在数轴上,它们所对应的数分别是-3和 且点A,B到原点的距离相等,求x的值.【解析】依题意可知, 解得:经检验, 是原方程的解.则x的值为
增根:在去分母,将分式方程转化为整式方程的过程中出现的不适合于原方程的根.
产生的原因:分式方程两边同乘以一个零因式后,所得的根是整式方程的根,而不是分式方程的根.所以我们解分式方程时一定要代入最简公分母检验
使最简公分母值为零的根
方程两边都乘以(x-1)(x+1),得x(x+1)+k(x+1)-x(x-1)=0解，得
当x=1时,原方程有增根，则k=-1
当x=-1时，k值不存在
∴当k=-1，原方程有增根。
“增根”是你可以求出来的，但代入后方程的分母为0无意义，原方程无解。“无解”包括增根和这个方程没有可解的根
思考：“方程有增根”和“方程无解”一样吗？