人教版七年级上册4.3.2 角的比较与运算课时练习

这是一份人教版七年级上册4.3.2 角的比较与运算课时练习，共15页。试卷主要包含了5∘，5)×30°=75°．等内容，欢迎下载使用。

班级：________ 姓名：________ 成绩：________

一．填空题（共10小题,共27分）
计算：48∘39′+67∘31′=． （2分）
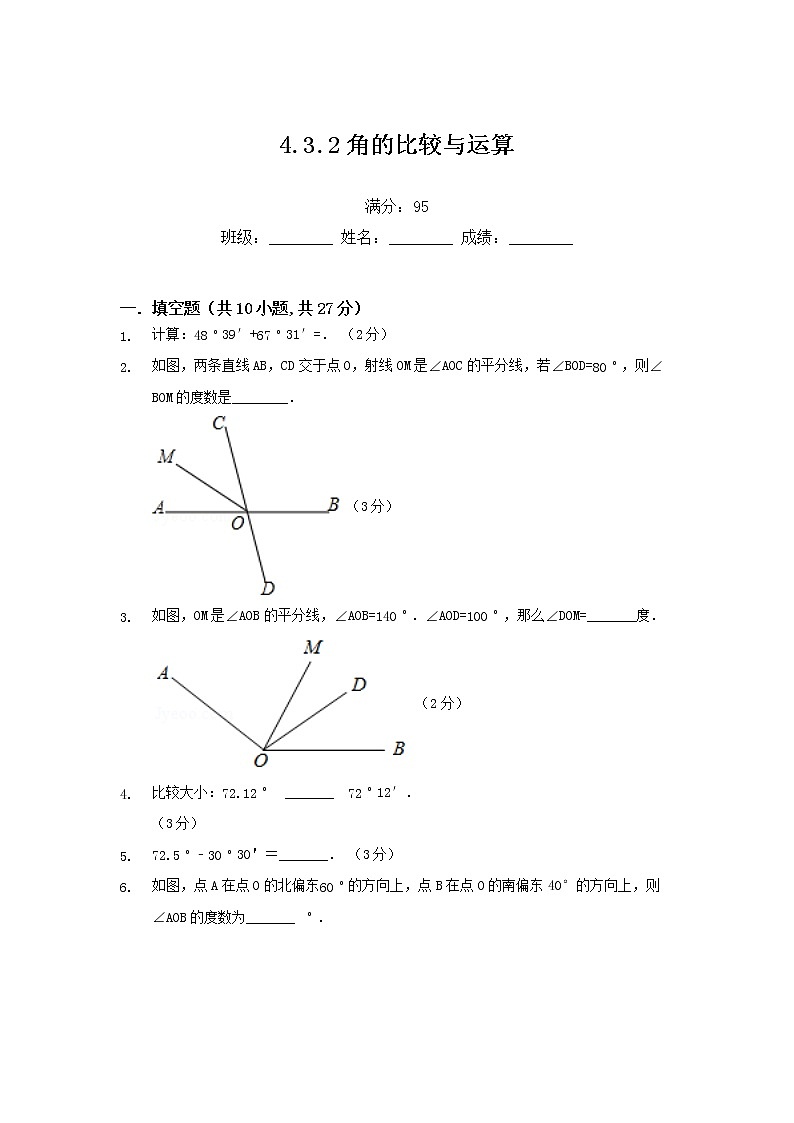
如图，两条直线AB，CD交于点O，射线OM是∠AOC的平分线，若∠BOD=80∘，则∠BOM的度数是________．
（3分）
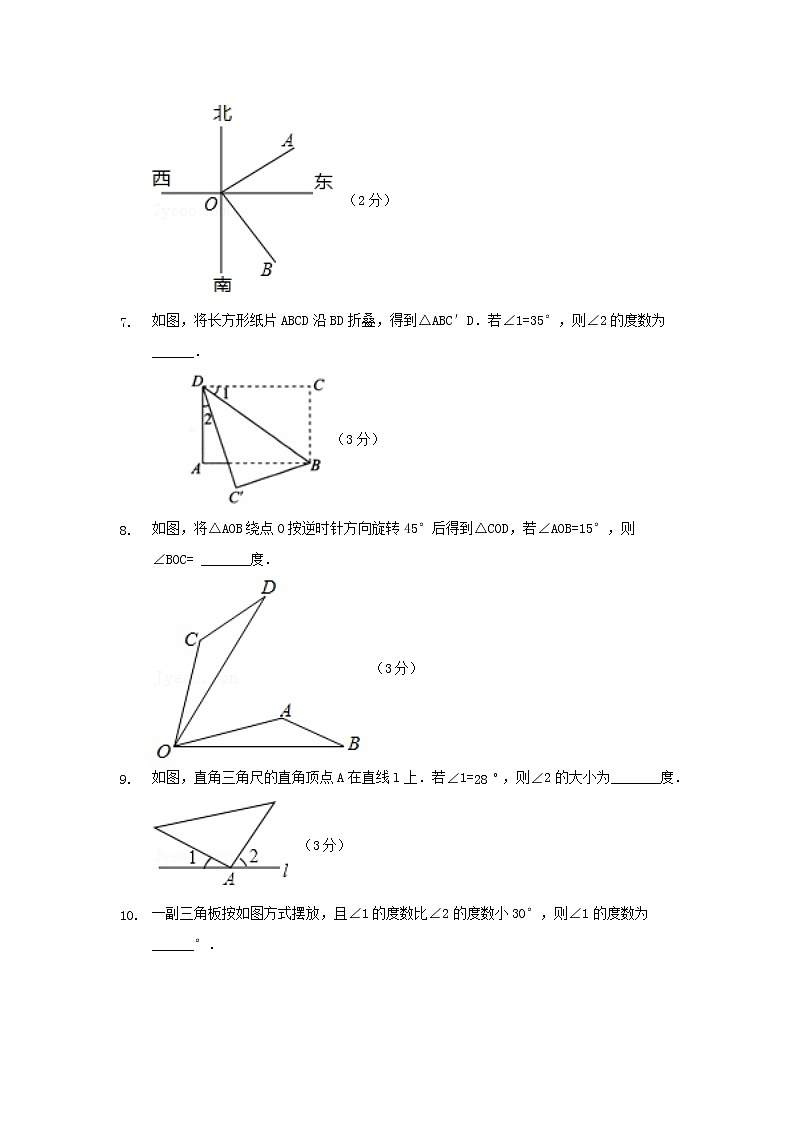
如图，OM是∠AOB的平分线，∠AOB=140∘．∠AOD=100∘，那么∠DOM=_______度．
（2分）
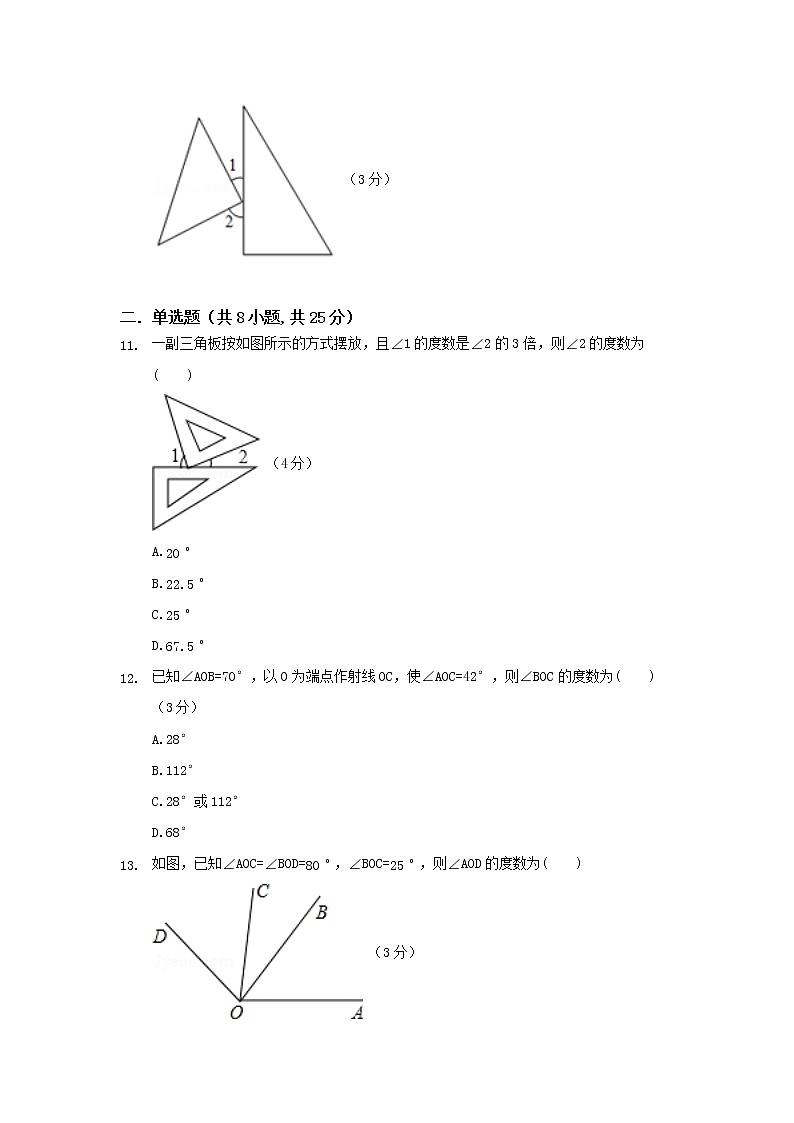
比较大小：72.12∘ _______ 72∘12′．
（3分）
72.5∘﹣30∘30＇＝_______． （3分）
如图，点A在点O的北偏东60∘的方向上，点B在点O的南偏东40°的方向上，则∠AOB的度数为_______ ​∘．
（2分）
如图，将长方形纸片ABCD沿BD折叠，得到△ABC′D．若∠1=35°，则∠2的度数为______．
（3分）
如图，将△AOB绕点O按逆时针方向旋转45°后得到△COD，若∠AOB=15°，则∠BOC= _______度．
（3分）
如图，直角三角尺的直角顶点A在直线l上．若∠1=28∘，则∠2的大小为_______度．
（3分）
一副三角板按如图方式摆放，且∠1的度数比∠2的度数小30°，则∠1的度数为______°．
（3分）

二．单选题（共8小题,共25分）
一副三角板按如图所示的方式摆放，且∠1的度数是∠2的3倍，则∠2的度数为( )
（4分）
A.20∘
B.22.5∘
C.25∘
D.67.5∘
已知∠AOB=70°，以O为端点作射线OC，使∠AOC=42°，则∠BOC的度数为( ) （3分）
A.28°
B.112°
C.28°或112°
D.68°
如图，已知∠AOC=∠BOD=80∘，∠BOC=25∘，则∠AOD的度数为( )
（3分）
A.150∘
B.145∘
C.140∘
D.135∘
如图，已知∠1=66°15′，则∠2的度数为( )
（3分）
A.113°45′
B.123°45′
C.23°45′
D.25°45′
如图，∠AOB=∠COD=90∘，∠AOD=146∘，则∠BOC的度数为( )
（3分）
A.43∘
B.34∘
C.56∘
D.50∘
八点三十分，这一时刻，时针与分针夹角是( )
（3分）
A.70∘
B.75∘
C.80∘
D.85∘
如图，O是直线AB上一点，OD平分∠BOC，∠COE=90∘，若∠AOC=40∘，则∠DOE为( )
（3分）
A.15∘
B.20∘
C.30∘
D.45∘
把一副三角板按如图所示那样拼在一起，那么∠ABC的度数是( )
（3分）
A.150∘
B.135∘
C.120∘
D.105∘

三．解答题（共5小题,共31分）
如图，已知，O是直线AB上一点，∠AOE=∠COD，射线OC平分∠BOE，∠EOC=50°．求∠DOE的度数．
（8分）
如图，O是直线AB上一点，OC是∠AOB的平分线，∠COD=31°28′，求∠AOD的度数．
（10分）
如图，已知∠BOC=140°，∠AOC=50°，OE平分∠BOC，OF平分∠AOC，求∠EOF的度数．
（5分）
计算：
34°25′×3+35°42′ （3分）
计算下列各题．
18°25′+105°38′ （5分）

四．解答题（组）（共1小题,共12分）
将一副三角板中的两块直角板中的两个直角顶点重合在一起，即按如图所示的方式叠放在一起，其中∠A=60∘，∠B=30∘，∠D=45∘．
（12分）
(1) 若∠BCD=45∘，求∠ACE的度数．
（4分）
(2) 若∠ACE=150∘，求∠BCD的度数．
（4分）
(3) 由(1)、(2)猜想∠ACE与∠BCD存在什么样的数量关系并说明理由．
（4分）

4.3.2角的比较与运算
参考答案与试题解析

一．填空题（共10小题）
第1题：
【正确答案】 116°10' 无
【答案解析】39′+31′=70′=1°10′，
故48°39′+67°31′=116°10'．
故答案为：116°10'．

第2题：
【正确答案】 140∘ 无
【答案解析】∵∠BOD=80°，
∴∠AOC=80°，∠COB=100°，
∵射线OM是∠AOC的平分线，
∴∠COM=40°，
∴∠BOM=40°+100°=140°，
故答案为：140°．

第3题：
【正确答案】 30 无
【答案解析】∵OM是∠AOB的平分线，∠AOB=140°，
∴ ，
∵∠AOD=100°，
∴∠DOM=∠AOD-∠AOM=100°-70°=30°．
故答案为：30．

第4题：
【正确答案】 ＜ 无
【答案解析】72°12′=72°+12′÷60=72.2°，
∴72.12°＜72°12′，
故答案为：＜．

第5题：
【正确答案】 42° 无
【答案解析】72.5°﹣30°30＇＝72°30＇﹣30°30＇＝42°．
故答案为：42°．

第6题：
【正确答案】 80 无
【答案解析】∵点A在点O的北偏东60°的方向上，点B在点O的南偏东40°的方向上，
∴∠AOB=180°-60°-40°=80°，
故答案为：80．

第7题：
【正确答案】 20° 无
【答案解析】∵∠1=∠BDC′=35°
∴∠2=90°-70°=20°．

第8题：
【正确答案】 60 无
【答案解析】∵将△AOB绕点O按逆时针方向旋转45°后得到△COD，
∴∠AOC=45°，
∴∠BOC=∠BOA+∠AOC=45°+15°=60°，
故答案为：60．

第9题：
【正确答案】 62 无
【答案解析】由题意可知，∠1+∠2=90°，
∴∠2=90°-∠1=90°-28°=62°．
故答案为：62．

第10题：
【正确答案】 30 无
【答案解析】根据题意可知，∠1+∠2=90°，
又∵∠1的度数比∠2的度数小30°，
∴∠2=∠1+30°，
∴∠1+(∠1+30°)=90°，
∴∠1=30°．
故答案为：30

二．单选题（共8小题）
第11题：
【正确答案】 B
【答案解析】根据图形得出：∠1+∠2=180°-90°=90°，
∵∠1的度数是∠2的3倍，
∴4∠2=90°，
∴∠2=22.5°，
故选：B．

第12题：
【正确答案】 C
【答案解析】解：如图，
当点C与点C1重合时，∠BOC=∠AOB-∠AOC=70°-42°=28°；
当点C与点C2重合时，∠BOC=∠AOB+∠AOC=70°+42°=112°．
故选C．

第13题：
【正确答案】 D
【答案解析】∵∠AOC=∠BOD=80°，∠BOC=25°，
∴∠AOB=∠AOC-∠BOC=80°-25°=55°，
∴∠AOD=∠BOD+∠AOB=80°+55°=135°，
故选：D．

第14题：
【正确答案】 A
【答案解析】180°-66°15′=113°45′

第15题：
【正确答案】 B
【答案解析】∠AOB=∠COD=90°，∠AOD=146°
则∠BOC=360°-2×90°-146°=34°
则∠BOC=34°．
故选：B．

第16题：
【正确答案】 B
【答案解析】∵八点三十分，时针指在8与9中间，分针指在数字6上，
∴时针与分针夹角是(2+0.5)×30°=75°．
故选：B．

第17题：
【正确答案】 B
【答案解析】∵∠AOC=40°，
∴∠BOC=180°-∠AOC=140°，
∵OD平分∠BOC，
∴∠COD= ∠BOC=70°，
∵∠COE=90°，
∴∠DOE=90°-70°=20°．
故选：B．

第18题：
【正确答案】 C
【答案解析】∠ABC=30°+90°=120°，
故选：C．

三．解答题（共5小题）
第19题：
【正确答案】 解：∵∠AOE=∠COD
∴∠AOE-∠DOE=∠COD-∠DOE，
即∠AOD=∠EOC=50°
∵射线OC平分∠BOE，
∴∠EOC=∠COB=50°
∴∠DOE=180°-3×50°=30°．
【答案解析】见答案

第20题：
【正确答案】 解：∠AOD=∠AOC-∠COD
=12 ∠AOB-∠COD
=90°-31°28′
=58°32′
【答案解析】见答案

第21题：
【正确答案】 解：因为∠BOC=140°，OE平分∠BOC，
所以．
因为∠AOC=50°，OF平分∠AOC，
所以．
所以∠EOF=∠COE-∠COF=70°-25°=45°．
【答案解析】见答案

第22题：
【正确答案】 解：34°25′×3+35°42′
=103°15′+35°42′
=138°57′
【答案解析】见答案

第23题：
【正确答案】 解：原式=123°63′=124°3′
【答案解析】见答案

四．解答题（组）（共1小题）
第24题：
第1小题:
【正确答案】 解：∵∠BCD=45°，∠ACB=90°，
∴∠ACD=∠ACB-∠DCB=45°，
又∵∠DCE=90°，
∴∠ACE=∠ACD+∠DCE=45°+90°=135°；
解：∵∠BCD=45°，∠ACB=90°，
∴∠ACD=∠ACB-∠DCB=45°，
又∵∠DCE=90°，
∴∠ACE=∠ACD+∠DCE=45°+90°=135°；
【答案解析】见答案

第2小题:
【正确答案】 解：∵∠ACE=150°，∠DCE=90°，
∴∠ACD=∠ACE-∠DCE=150°-90°=60°，
又∵∠ACB=90°，
∴∠BCD=∠ACB-∠ACD=90°-60°=30°
解：∵∠ACE=150°，∠DCE=90°，
∴∠ACD=∠ACE-∠DCE=150°-90°=60°，
又∵∠ACB=90°，
∴∠BCD=∠ACB-∠ACD=90°-60°=30°
【答案解析】见答案

第3小题:
【正确答案】 解：由(1)、(2)猜想∠ACE与∠BCD互补．
理由：∵∠BCD=∠ACB-∠ACD=90°-∠ACD，∠ACE=∠DCE+∠ACD=90°+∠ACD，
∴∠BCD+∠ACE=90°-∠ACD+90°+∠ACD=180°，
∴∠ACE与∠BCD互补．
解：由(1)、(2)猜想∠ACE与∠BCD互补．
理由：∵∠BCD=∠ACB-∠ACD=90°-∠ACD，∠ACE=∠DCE+∠ACD=90°+∠ACD，
∴∠BCD+∠ACE=90°-∠ACD+90°+∠ACD=180°，
∴∠ACE与∠BCD互补．
【答案解析】见答案