






初中数学人教版九年级下册28.1 锐角三角函数完整版课件ppt
展开28.1(1) 锐角三角函数 正弦 同步练习
知识点1 正弦函数
1.(2020·重庆·九年级期中)如图,在中,,,,则的值为( )
A. B. C. D.
2.(2021·安徽肥西·九年级期末)在Rt△ABC中,各边都扩大3倍,则锐角A的正弦值( )
A.扩大3倍 B.缩小3倍 C.不变 D.不能确定
3.(2021·全国·九年级课时练习)如图,在Rt中,CD是斜边AB上的高,,则下列比值中不等于的是( )
A. B. C. D.
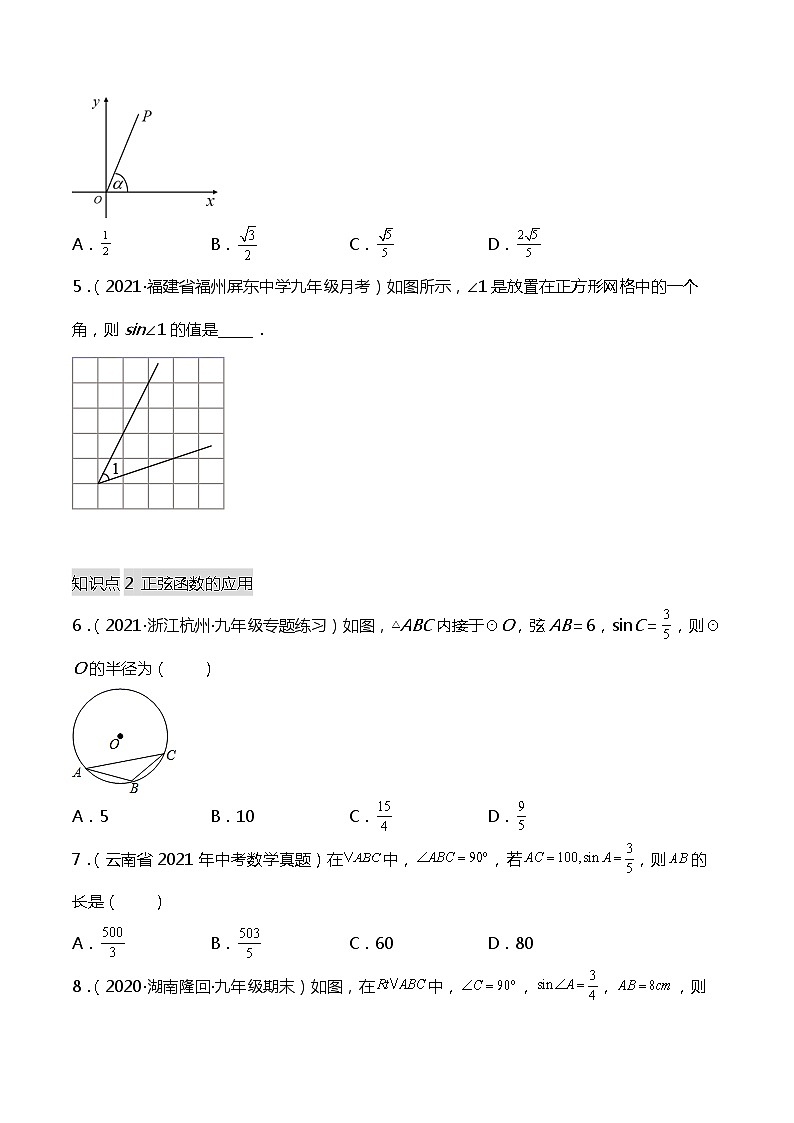
4.(2021·江苏·九年级专题练习)如图,平面直角坐标系中的点P的坐标为,与x轴正半轴的夹角为,则的值为( )
A. B. C. D.
5.(2021·福建省福州屏东中学九年级月考)如图所示,∠1是放置在正方形网格中的一个角,则sin∠1的值是_____.
知识点2 正弦函数的应用
6.(2021·浙江杭州·九年级专题练习)如图,△ABC内接于⊙O,弦AB=6,sinC=,则⊙O的半径为( )
A.5 B.10 C. D.
7.(云南省2021年中考数学真题)在中,,若,则的长是( )
A. B. C.60 D.80
8.(2020·湖南隆回·九年级期末)如图,在中,,,,则的面积是( )
A. B. C. D.
9.(2018·吉林·中考模拟)已知:如图,AB与⊙O相切于点C,OA=OB,⊙O的直径为4,AB=8.
(1)求OB的长;
(2)求sinA的值.
素质提升
10.(2021·陕西碑林·九年级期中)已知△ABC中,AC=4,BC=3,AB=5,则sinB=( )
A. B. C. D.
11.(2021·贵州德江·九年级期中)如图,在Rt△ABC中,∠C=90°,,则sinB的值为( )
A. B. C. D.2
12.(2020·山东·肥城市湖屯镇初级中学九年级月考)如图,在矩形中,,,点在上,将矩形沿折叠,点恰好落在边上的点处,那么的值为( ).
A. B. C. D.
13.(江苏省扬州市2020年中考数学试题)如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C、D,则的值为( )
A. B. C. D.
14.(2021·江苏溧阳·九年级期末)如图,在2×4的方格中,两条线段的夹角(锐角)为∠1,则sin∠1=______________.
15.(浙江省湖州市2021年中考数学真题)如图,已知是⊙的直径,是所对的圆周角,.
(1)求的度数;
(2)过点作,垂足为,的延长线交⊙于点.若,求的长.
16.(山东省菏泽市2021年中考数学真题)如图,在中,是直径,弦,垂足为,为上一点,为弦延长线上一点,连接并延长交直径的延长线于点,连接交于点,若.
(1)求证:是的切线;
(2)若的半径为8,,求的长.
28.1.1 正弦 参考答案
知识点1 正弦函数
1.(2020·重庆·九年级期中)如图,在中,,,,则的值为( )
A. B. C. D.
【答案】A
【分析】
根据锐角三角函数的定义得出sinB= ,代入即可得出答案.
【详解】
解:∵在△ABC中,∠C=90°,AC=3,AB=5,
∴sinB== ,
故选A.
【点睛】
本题考查了锐角三角函数的定义的应用,主要考查学生对锐角三角函数的定义的理解和记忆,题目比较典型.
2.(2021·安徽肥西·九年级期末)在Rt△ABC中,各边都扩大3倍,则锐角A的正弦值( )
A.扩大3倍 B.缩小3倍 C.不变 D.不能确定
【答案】C
【分析】
根据锐角三角函数的定义,可得答案.
【详解】
解:由题意,得
Rt△ABC中,各边都扩大3倍,则锐角A的正弦值不变,
故选:C.
【点睛】
本题考查了正弦函数的概念,属于简单题.理解正弦函数的定义是解题关键.
3.(2021·全国·九年级课时练习)如图,在Rt中,CD是斜边AB上的高,,则下列比值中不等于的是( )
A. B. C. D.
【答案】D
【分析】
利用锐角三角函数定义判断即可.
【详解】
在中, ,
在中, ,
, ,
,
在中,,
故选:D.
【点睛】
此题考查了锐角三角函数的定义,熟练掌握锐角三角函数定义是解本题的关键.
4.(2021·江苏·九年级专题练习)如图,平面直角坐标系中的点P的坐标为,与x轴正半轴的夹角为,则的值为( )
A. B. C. D.
【答案】D
【分析】
如图,过作轴于由 可得 再利用勾股定理求解 结合 从而可得答案.
【详解】
解:如图,过作轴于
故选:
【点睛】
本题考查的是平面直角坐标系内点的坐标含义,锐角三角函数的应用,掌握构造直角三角形求解锐角三角函数是解题的关键.
5.(2021·福建省福州屏东中学九年级月考)如图所示,∠1是放置在正方形网格中的一个角,则sin∠1的值是_____.
【答案】
【分析】
先利用勾股定理的逆定理证明△ABC直角三角形,然后利用正弦的定义求解.
【详解】
解:如图,∵AC=,BC=,AB=,
∴AC2+BC2=AB2,
∴△ABC为等腰直角三角形,
∴sin∠1=sin45°=.
故答案为.
【点睛】
本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.灵活应用勾股定理和锐角三角函数.也考查了勾股定理的逆定理.
知识点2 正弦函数的应用
6.(2021·浙江杭州·九年级专题练习)如图,△ABC内接于⊙O,弦AB=6,sinC=,则⊙O的半径为( )
A.5 B.10 C. D.
【答案】A
【分析】
过B作直径BD,连接AD,如图,根据圆周角定理和三角函数的定义即可得到结论.
【详解】
解:过B作直径BD,连接AD,
∵BD为直径,
∴∠BAD=90°,
∵∠D=∠C,
∴sinD=sinC=,
∵AB=6,
∴BD=10,
∴⊙O的半径为5,
故选:A.
【点睛】
本题考查了圆周角定理和解直角三角形,正确的作出辅助线,构造直角三角形是解题的关键.
7.(云南省2021年中考数学真题)在中,,若,则的长是( )
A. B. C.60 D.80
【答案】D
【分析】
根据三角函数的定义得到BC和AC的比值,求出BC,然后利用勾股定理即可求解.
【详解】
解:∵∠ABC=90°,sin∠A==,AC=100,
∴BC=100×3÷5=60,
∴AB==80,
故选D.
【点睛】
本题主要考查的是解直角三角形,掌握勾股定理和正弦函数的定义是解题的关键.
8.(2020·湖南隆回·九年级期末)如图,在中,,,,则的面积是( )
A. B. C. D.
【答案】C
【分析】
在Rt△ABC中,求出BC,AC即可解决问题.
【详解】
解:在Rt△ACB中,∵∠C=90°,AB=8cm,
∴sinA==,
∴BC=6(cm),
∴AC=(cm),
∴S△ABC=•BC•AC=×6×2=6(cm2).
故选:C.
【点睛】
本题考查解直角三角形的应用,三角形的面积等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
9.(2018·吉林·中考模拟)已知:如图,AB与⊙O相切于点C,OA=OB,⊙O的直径为4,AB=8.
(1)求OB的长;
(2)求sinA的值.
【答案】(1)(2)
【解析】
试题分析:(1)先由OA=OB可知△OAB是等腰三角形,再根据切线的性质可知OC⊥AB,故可求出BC的长,再利用勾股定理求出OB的长即可.
(2)根据OA=OB求出OA的长,再根据角的三角函数值求出sinA的值即可.
试题解析:(1)由已知,OC=2,BC=4.
在Rt△OBC中,由勾股定理,得
;
(2)在Rt△OAC中,
∵OA=OB=,OC=2,
∴sinA=.
考点:1、切线的性质;2、勾股定理
素质提升
10.(2021·陕西碑林·九年级期中)已知△ABC中,AC=4,BC=3,AB=5,则sinB=( )
A. B. C. D.
【答案】B
【分析】
根据勾股定理逆定理以及正弦的定义求解即可.
【详解】
解:∵△ABC中,AC=4,BC=3,AB=5,即42+32=52,
∴△ABC是直角三角形,∠C=90°.
sinB=.
故选B.
【点睛】
本题考查勾股定理逆定理以及正弦的定义,熟练掌握三角函数的定义是解题关键.
11.(2021·贵州德江·九年级期中)如图,在Rt△ABC中,∠C=90°,,则sinB的值为( )
A. B. C. D.2
【答案】A
【分析】
根据勾股定理,可得AB与BC的关系,根据正弦函数的定义,可得答案.
【详解】
解:∵∠C=90°,,
∴,
,
故选A.
【点睛】
本题考查了锐角三角函数的定义,先利用勾股定理得出BA与BC的关系,再利用正弦函数的定义.
12.(2020·山东·肥城市湖屯镇初级中学九年级月考)如图,在矩形中,,,点在上,将矩形沿折叠,点恰好落在边上的点处,那么的值为( ).
A. B. C. D.
【答案】B
【分析】
根据折叠的性质,得,,由勾股定理得,进而得,设,则,根据勾股定理,列出方程,求出x的值,即可得到答案.
【详解】
∵四边形为矩形,∴,.
∵矩形沿直线折叠,顶点恰好落在边上的处,
∴,,
∵在中,,
∴,
设,则,
∵在中, ,
∴,解得:,
∴,
∴.
故选B.
【点睛】
本题主要考查矩形中折叠的性质以及勾股定理和正弦三角函数的定义,掌握勾股定理,列方程,是解题的关键.
13.(江苏省扬州市2020年中考数学试题)如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C、D,则的值为( )
A. B. C. D.
【答案】A
【分析】
首先根据圆周角定理可知,∠ABC=,在Rt△ACB中,根据锐角三角函数的定义求出∠ABC的正弦值.
【详解】
∵和∠ABC所对的弧长都是,
∴根据圆周角定理知,∠ABC=,
∴在Rt△ACB中,AB=
根据锐角三角函数的定义知,sin∠ABC=,
∴=,
故选A.
【点睛】
本题主要考查锐角三角函数的定义和圆周角的知识点,解答本题的关键是利用圆周角定理把求的正弦值转化成求∠ABC的正弦值,本题是一道比较不错的习题.
14.(2021·江苏溧阳·九年级期末)如图,在2×4的方格中,两条线段的夹角(锐角)为∠1,则sin∠1=______________.
【答案】
【分析】
解:如图添加字母,过A作AB∥ED,可得∠1=∠CAB,连结BC,在△ABC中由勾股定理AC=,AB =,BC=,由AB2+BC2=5+5=10=AC2,证得∠ABC=90°,由AB=BC可得∠CAB=45°,利用三角函数定义sin∠CAB=。
【详解】
解:如图添加字母,过A作AB∥ED,使AB=ED,
∠1=∠CAB,
连结BC,
在△ABC中,
AC=,
AB =,BC=,
∵AB2+BC2=5+5=10=AC2,
∴∠ABC=90°,AB=BC,
∴∠CAB=45°,
sin∠CAB,
故答案为:.
【点睛】
本题主要考查了勾股定理及逆定理,以及锐角三角函数关系,正确得出是直角三角形是解题关键.
15.(浙江省湖州市2021年中考数学真题)如图,已知是⊙的直径,是所对的圆周角,.
(1)求的度数;
(2)过点作,垂足为,的延长线交⊙于点.若,求的长.
【答案】(1);(2)
【分析】
(1)连结,根据圆周角性质,得;根据直径所对圆周角为直角、直角三角形两锐角互余的性质计算,即可得到答案;
(2)根据含角的直角三角形性质,得;根据垂径定理、特殊角度三角函数的性质计算,即可得到答案.
【详解】
(1)连结,
是的直径,
,
(2),,
∴
,,且是直径
.
【点睛】
本题考查了圆、含角的直角三角形、三角函数的知识;解题的关键是熟练掌握圆周角、垂径定理、含角的直角三角形、三角函数、直角三角形两锐角互余的性质,从而完成求解.
16.(山东省菏泽市2021年中考数学真题)如图,在中,是直径,弦,垂足为,为上一点,为弦延长线上一点,连接并延长交直径的延长线于点,连接交于点,若.
(1)求证:是的切线;
(2)若的半径为8,,求的长.
【答案】(1)见解析;(2)
【分析】
(1)连接OE,证明OE⊥EF即可;
(2)由证得,运用正弦的概念可得结论.
【详解】
解:(1)证明:连接OE,如图,
∵OA=OE
∴∠OAE=∠OEA.
∵EF=PF,
∴∠EPF=∠PEF
∵∠APH=∠EPF,
∴∠APH=∠EPF,
∴∠AEF=∠APH.
∵CD⊥AB,
∴∠AHC=90°.
∴∠OAE+∠APH=90°.
∴∠OEA+∠AEF=90°
∴∠OEF=90°
∴OE⊥EF.
∵OE是的半径
∴EF是圆的切线,
(2)∵CD⊥AB
∴是直角三角形
∵
∴
设,则
由勾股定理得,
由(1)得,是直角三角形
∴
∴,即
∵
∴
解得,
【点睛】
此题主要考查了圆的切线的判定,勾股定理和解直角三角形等知识,熟练掌握切线的判定是解答此题的关键.
人教版九年级下册第二十八章 锐角三角函数28.1 锐角三角函数教案配套课件ppt: 这是一份人教版九年级下册<a href="/sx/tb_c10296_t3/?tag_id=26" target="_blank">第二十八章 锐角三角函数28.1 锐角三角函数教案配套课件ppt</a>,共26页。PPT课件主要包含了正弦的定义,知识点1,故AB,你发现了什么,正弦的表示,知识点2,因此sinA,sinB,基础巩固,综合应用等内容,欢迎下载使用。
初中人教版28.1 锐角三角函数获奖课件ppt: 这是一份初中人教版28.1 锐角三角函数获奖课件ppt,文件包含281锐角三角函数第3课时特殊角的锐角三角函数pptx、281锐角三角函数第3课时特殊角的锐角三角函数导学案doc、281锐角三角函数第3课时特殊角的锐角三角函数教案doc等3份课件配套教学资源,其中PPT共41页, 欢迎下载使用。
初中数学人教版九年级下册28.1 锐角三角函数精品ppt课件: 这是一份初中数学人教版九年级下册28.1 锐角三角函数精品ppt课件,文件包含281锐角三角函数第1课时正弦pptx、281锐角三角函数第1课时正弦教案doc、281锐角三角函数第1课时正弦导学案doc等3份课件配套教学资源,其中PPT共26页, 欢迎下载使用。














