人教版八年级上册第十一章 三角形11.1 与三角形有关的线段11.1.2 三角形的高、中线与角平分线教学演示课件ppt

这是一份人教版八年级上册第十一章 三角形11.1 与三角形有关的线段11.1.2 三角形的高、中线与角平分线教学演示课件ppt，共13页。PPT课件主要包含了情境问题，探究新知，实践应用1，实践应用2，小结与作业等内容，欢迎下载使用。

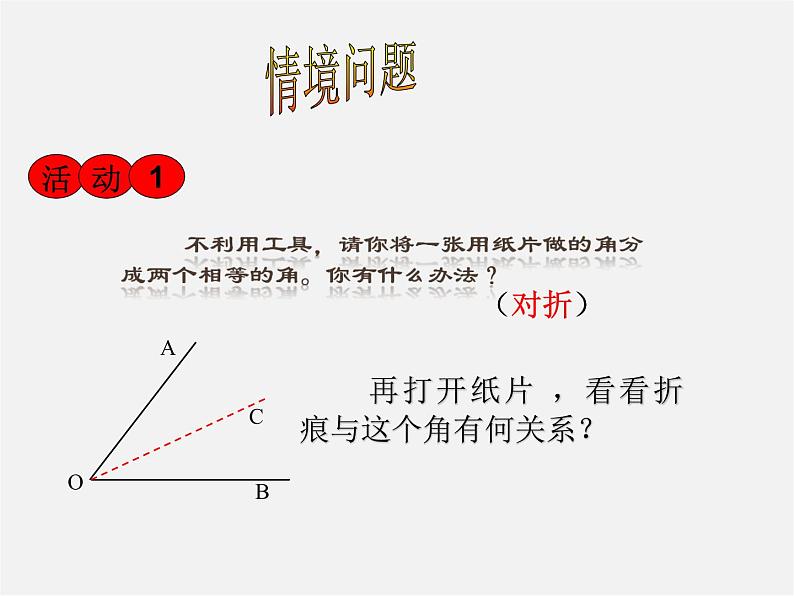
再打开纸片 ，看看折痕与这个角有何关系？
1、如图，是一个角平分仪，其中AB=AD,BC=DC。将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线，你能说明它的道理吗?
如果前面活动中的纸片换成木板、钢板等没法折的角，又该怎么办呢？
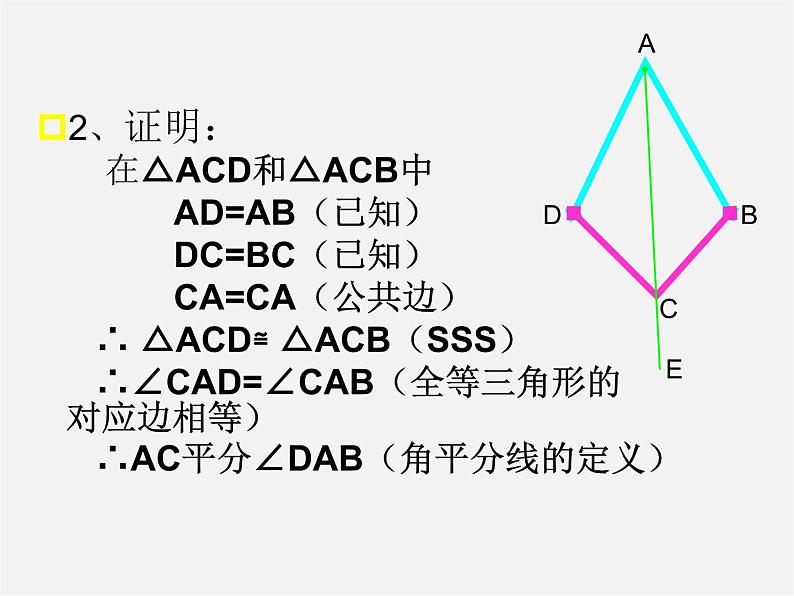
2、证明： 在△ACD和△ACB中 AD=AB（已知） DC=BC（已知） CA=CA（公共边） ∴ △ACD≌ △ACB（SSS） ∴∠CAD=∠CAB（全等三角形的 对应边相等） ∴AC平分∠DAB（角平分线的定义）
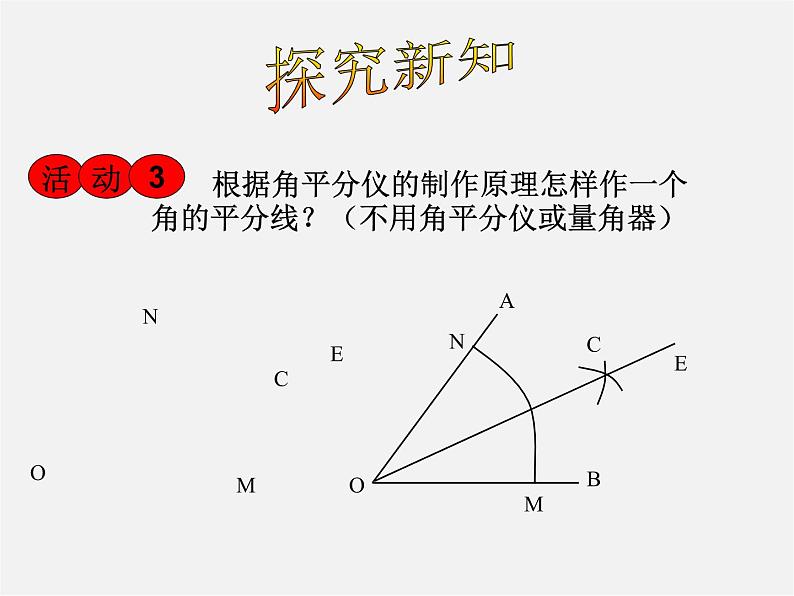
根据角平分仪的制作原理怎样作一个角的平分线？（不用角平分仪或量角器）
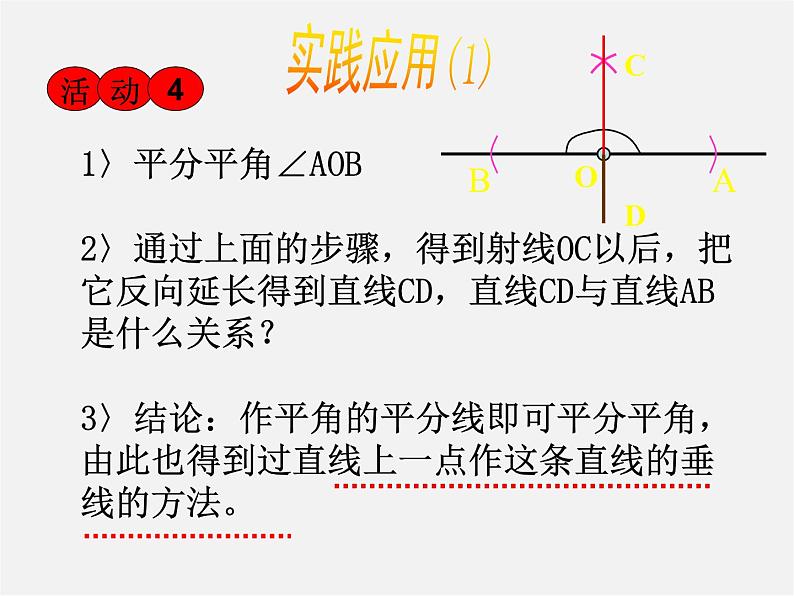
1〉平分平角∠AOB2〉通过上面的步骤，得到射线OC以后，把它反向延长得到直线CD，直线CD与直线AB是什么关系？ 3〉结论：作平角的平分线即可平分平角，由此也得到过直线上一点作这条直线的垂线的方法。
(1)实验：将∠AOB对折，再折出一个直角三角形（使第一条折痕为斜边），然后展开，观察两次折叠形成的三条折痕，你能得出什么结论？
(2)猜想:角的平分线上的点到角的两边的距离相等.
证明：∵OC平分∠ AOB ∠ AOB （已知） ∴ ∠1= ∠2（角平分线的定义） ∵PD ⊥ OA，PE ⊥ OB（已知） ∴ ∠PDO= ∠PEO（垂直的定义） 在△PDO和△PEO中 ∠PDO= ∠PEO（已证） ∠1= ∠2 （已证） OP=OP （公共边） ∴ △PDO ≌ △PEO（AAS） ∴PD=PE（全等三角形的对应边相等）
已知：如图，OC平分∠AOB，点P在OC上，PD⊥OA于点D，PE⊥OB于点E求证: PD=PE
角平分线上的点到角两边的距离相等。
(4)得到角平分线的性质：
利用此性质怎样书写推理过程?
思考：要在Ｓ区建一个集贸市场，使它到公路，铁路距离相等且离公路，铁路的交叉处５００米，应建在何处？（比例尺 1：20 000）
如图：在△ABC中，∠C=90° AD是∠BAC的平分线，DE⊥AB于E，F在AC上，BD=DF； 求证：CF=EB
分析:要证CF=EB,首先我们想到的是要证它们所在的两个三角形全等,即Rt△CDF ≌ Rt△EDB.
现已有一个条件BD=DF(斜边相等),还需要我们找什么条件
DC=DE (因为角的平分线的性质) 再用HL证明.
试试自己写证明。你一定行！
一、过程小结：情境→观察→作图→应用→探究→再应用
二、知识小结：本节课学习了那些知识？有哪些运用？你学了吗？做了吗？用了吗？