数学12.2 三角形全等的判定教学课件ppt

这是一份数学12.2 三角形全等的判定教学课件ppt，共17页。PPT课件主要包含了用数学语言表述，复习回顾，探究新知⑴，⑴边－角－边，做一做，动画演示，几何语言，ABDE，∠B∠E，BCEF等内容，欢迎下载使用。
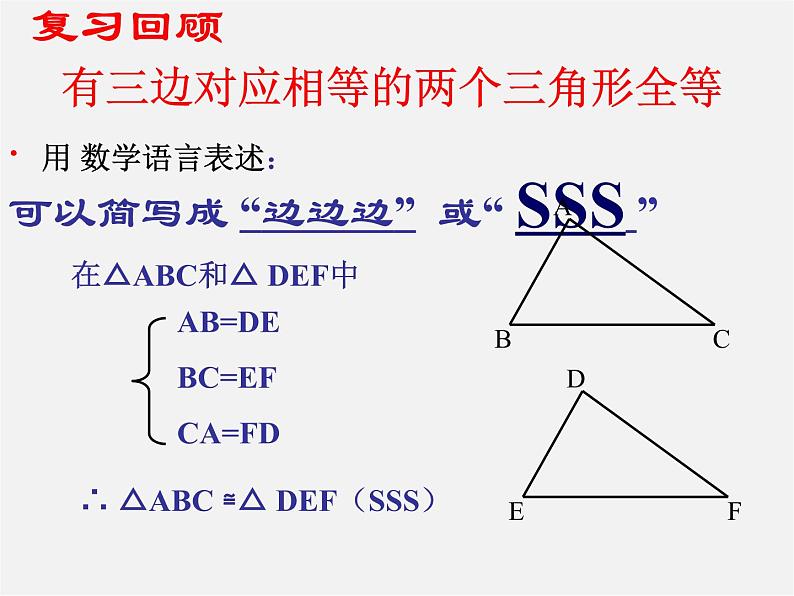
有三边对应相等的两个三角形全等.可以简写成 “边边边” 或“ SSS ”
在△ABC和△ DEF中
∴ △ABC ≌△ DEF（SSS）
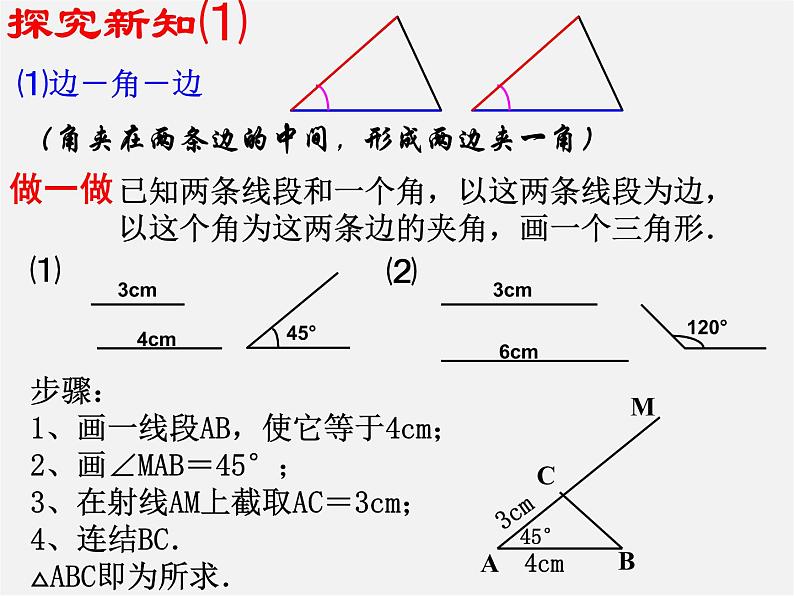
（角夹在两条边的中间，形成两边夹一角）
已知两条线段和一个角，以这两条线段为边，以这个角为这两条边的夹角，画一个三角形．
步骤：　1、画一线段AB，使它等于4cm；2、画∠MAB＝45°；3、在射线AM上截取AC＝3cm；4、连结BC．△ABC即为所求．
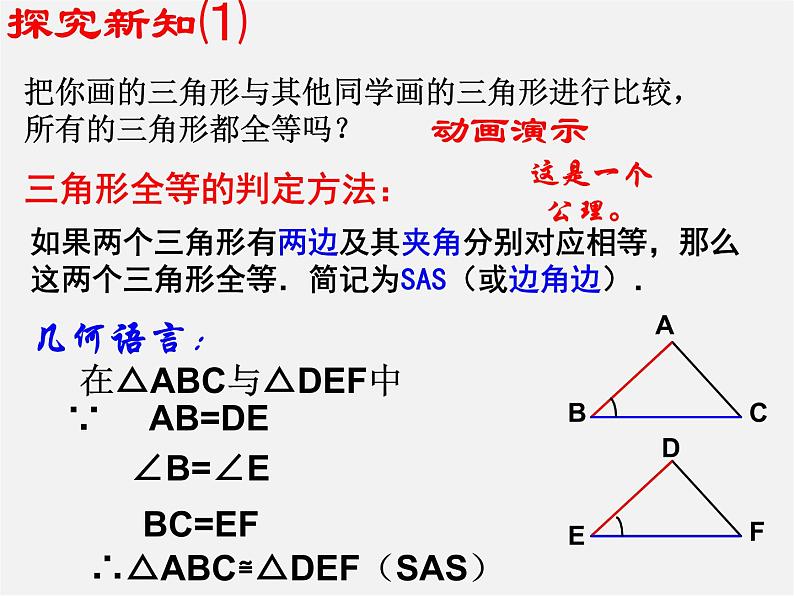
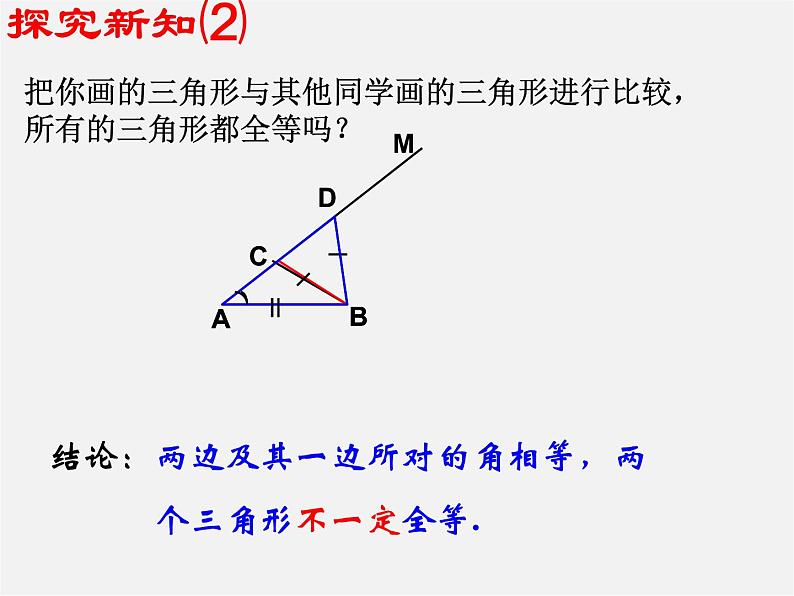
把你画的三角形与其他同学画的三角形进行比较，所有的三角形都全等吗？
如果两个三角形有两边及其夹角分别对应相等，那么这两个三角形全等．简记为SAS（或边角边）．
三角形全等的判定方法：
在△ABC与△DEF中
∴△ABC≌△DEF（SAS）
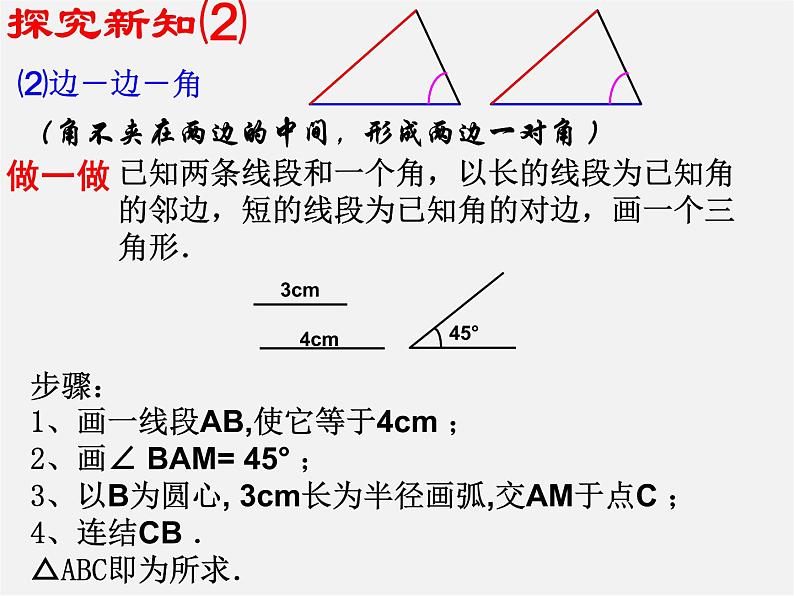
（角不夹在两边的中间，形成两边一对角 ）
已知两条线段和一个角，以长的线段为已知角的邻边，短的线段为已知角的对边，画一个三角形．
步骤：　1、画一线段AB,使它等于4cm ；2、画∠ BAM= 45° ；3、以B为圆心, 3cm长为半径画弧,交AM于点C ；4、连结CB ．△ABC即为所求．
结论：两边及其一边所对的角相等，两 个三角形不一定全等.
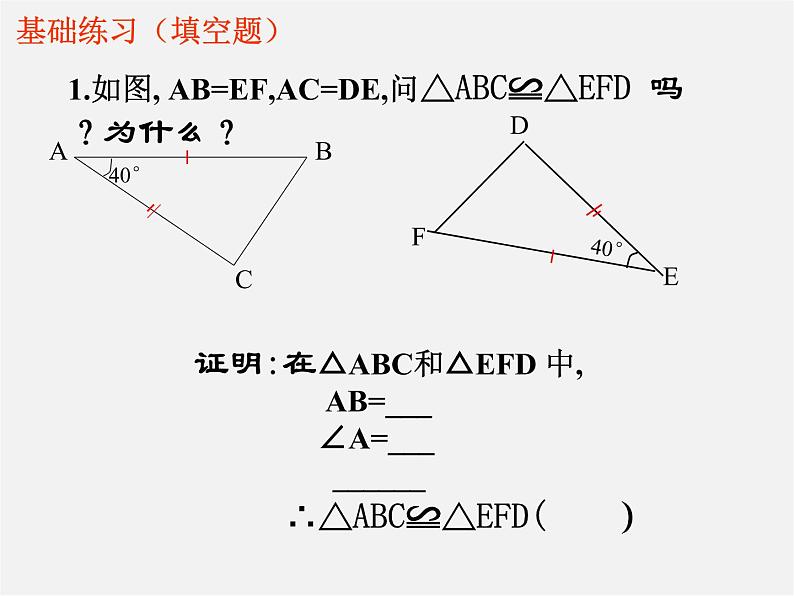
1.如图, AB=EF,AC=DE,问△ABC≌△EFD 吗？为什么？
证明:在△ABC和△EFD 中, AB=___ ∠A=___ ______ ∴△ABC≌△EFD( ）
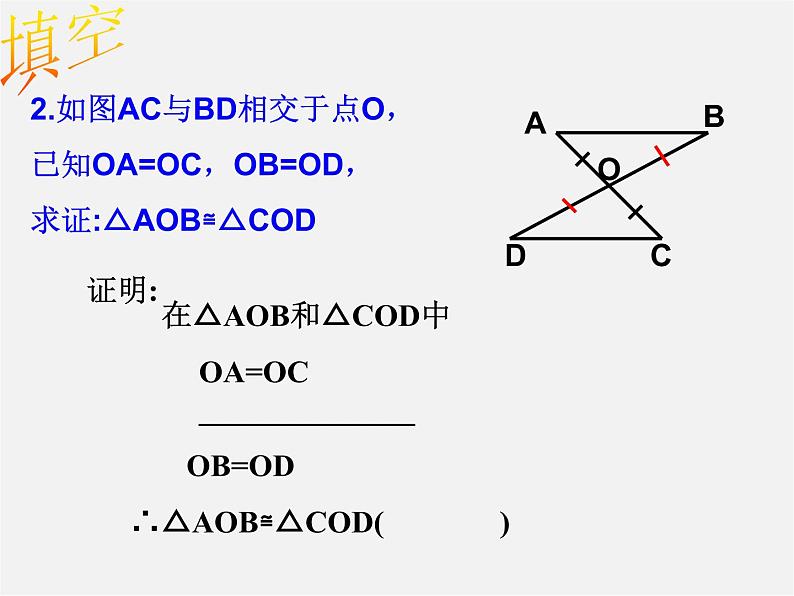
2.如图AC与BD相交于点O，已知OA=OC，OB=OD，求证:△AOB≌△COD
在△AOB和△COD中
OA=OC______________
∴△AOB≌△COD( )
已知：如图，AB=CB，∠1=∠2 △ABD 和△CBD 全等吗？
例2如图有一池塘，要测池塘两端A,B的距离，可先在平地上取一点C，从点C不经过池塘可以直接到达点A和B。连接AC并延长到点D，使CD=CA,连接BC并延长到点E，使CE=CB，连接DE,那么量出DE的长就是A,B的距离，为什么？
变式1:已知：如图,AB=CB,∠1= ∠2 求证:(1) AD=CD (2)BD 平分∠ ADC
变式2:已知:AD=CD，BD平分∠ADC 求证:∠A=∠C
例3: 如图，AC=BD，∠1= ∠2求证:BC=AD
变式1: 如图，AC=BD,BC=AD求证:∠1= ∠2
变式2: 如图，AC=BD,BC=AD求证:∠C=∠D
变式3: 如图，AC=BD,BC=AD求证:∠A=∠B
1.如图，点E，F在BC上，BE=CF，AB=DC，∠B=∠C求证：∠A=∠D
2.如图，已知OA=OB,应填什么条件就得到： △AOC≌ △BOD(只允许添加一个条件)
AB=DE∠B=∠EBC=EF
两边和它们的夹角对应相等的两个三角形全等。简写成“边角边”或“SAS”