初中数学苏科版七年级下册第7章 平面图形的认识（二）7.5 多边形的内角和与外角和教学ppt课件

这是一份初中数学苏科版七年级下册第7章 平面图形的认识（二）7.5 多边形的内角和与外角和教学ppt课件，共19页。PPT课件主要包含了学习目标，三角形的外角，探究与思考，相邻的内角，不相邻的内角，判断基础巩固，多边形的外角和，观察与思考，动态展示，多边形外角和实际应用等内容，欢迎下载使用。

学习目标1、利用多种的方法探索多边形的外角和公式。2、利用多边形外角和公式解决问题。重点探索多边形的外角和公式。难点利用多边形外角和公式解决问题。
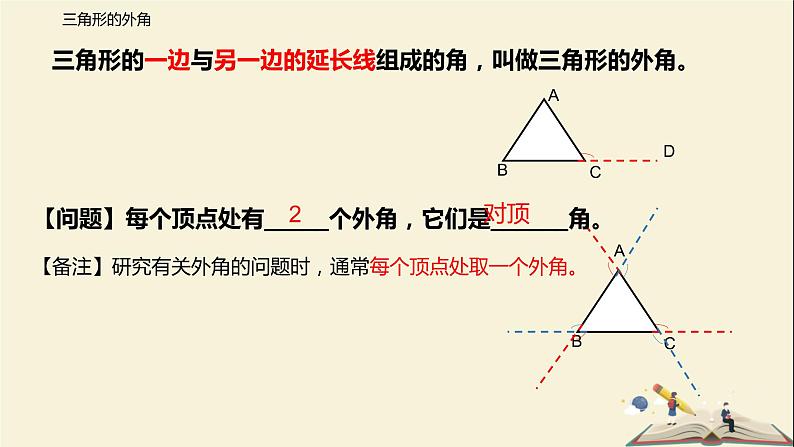
三角形的一边与另一边的延长线组成的角，叫做三角形的外角。
【问题】每个顶点处有_____个外角，它们是______角。
【备注】研究有关外角的问题时，通常每个顶点处取一个外角。
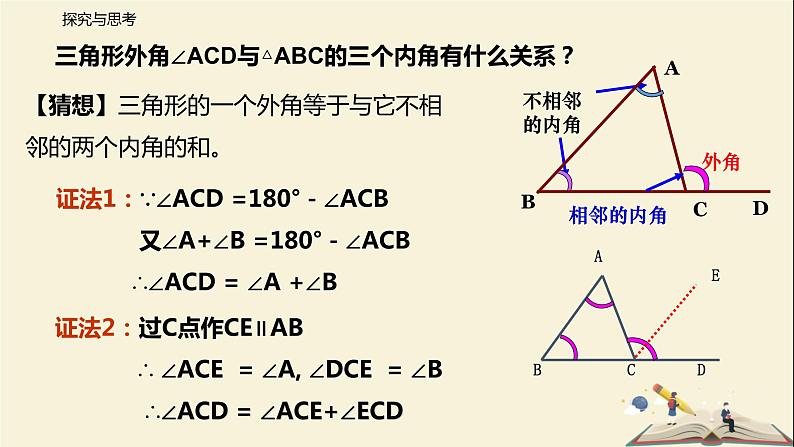
三角形外角∠ACD与△ABC的三个内角有什么关系？
【猜想】三角形的一个外角等于与它不相 邻的两个内角的和。
证法1：∵∠ACD =180°－∠ACB 又∠A+∠B =180°－∠ACB ∴∠ACD = ∠A +∠B
证法2：过C点作CE∥AB ∴ ∠ACE = ∠A, ∠DCE = ∠B ∴∠ACD = ∠ACE+∠ECD
三角形的外角与内角的关系：1、三角形的一个外角与它相邻的内角 ；2、三角形的一个外角 与它不相邻的两个内角的和（三角形外角的性质1）；3、三角形的一个外角 任何一个与它不相邻的内角。
1.三角形的外角和是指三角形所有外角和。2.三角形的外角和等于它内角和的2倍。3.三角形的一个外角等于两个内角的和。4、三角形的一个外角等于与它不相邻的两个内角的和。5.三角形的一个外角大于任何一个内角。6.三角形的一个外角大于任何一个不相邻的内角。
练一练（利用三角形外角的性质解题）
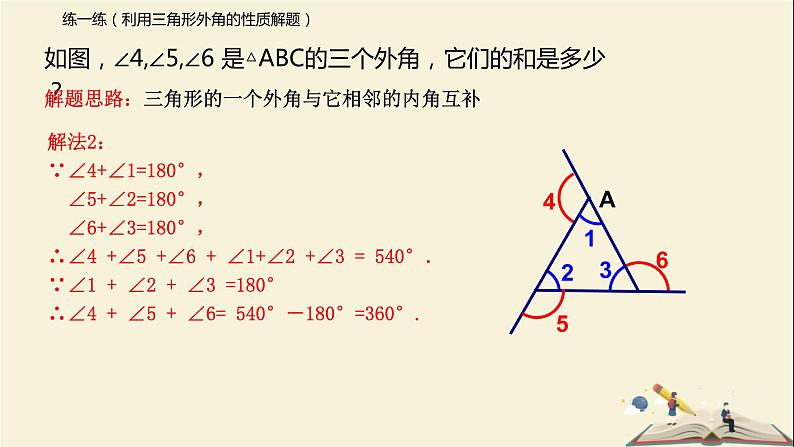
如图，∠4,∠5,∠6 是△ABC的三个外角，它们的和是多少？
解法1：∵ ∠4 =∠2 +∠3， ∠5 =∠1 +∠3， ∠6 =∠1 +∠2，∴∠4 +∠5 +∠6=(∠2+∠3)+(∠1+∠3)+(∠1+∠2)= 2(∠1+∠2+∠3)．= 2×180°=360°
解题思路：三角形的一个外角等于与它不相邻的两个内角的和
解法2：∵∠4+∠1=180°， ∠5+∠2=180°， ∠6+∠3=180°，∴∠4 +∠5 +∠6 + ∠1+∠2 +∠3 = 540°． ∵∠1 + ∠2 + ∠3 =180°∴∠4 + ∠5 + ∠6= 540°－180°=360°.
解题思路：三角形的一个外角与它相邻的内角互补
解法3：过A作AD∥BC， ∴ ∠5＝∠BAD， ∠6＝∠8. ∴ ∠4＋∠5＋∠6＝∠4＋∠BAD＋∠8=360°
解题思路：两直线平行，同位角相等
三角形外角性质2：三角形的外角和等于360°.
在六边形的每个顶点处各取一个外角，这些外角的和叫做六边形外角和。
问题1：任何一个外角同与它相邻的内角有什么关系？
问题2：六边形的6个外角加上与它们相邻的内角，所得总和是多少？
单个外角和它相邻的内角和为180°，所以六边形6个外角与它们相邻内角和为6×180°=1080°
问题3：上述总和与六边形的内角和、外角和有什么关系？
6×180°-（n-2）×180°=360°
n边形的外角和是多少度呢?
因为多边形的外角与它相邻的内角是邻补角，所以n边形的外角和加内角和等于n·180°，而内角和为(n－2)·180°,则外角和为：n·180°－(n－2)·180°= 360°.
多边形的外角和等于360°.
动态演示多边形外角和为360°
将左侧的五边形不断缩小后，形成右边图形。由各线段组成夹角和为一个周角，所以多边形外角和为360°
如图所示，小华从A点出发，沿直线前进10米后左转24°，再沿直线前进10米，又向左转24°，……，照这样走下去，他第一次回到出发地A点时，一共走的路程是（　 　）A．140米B．150米C．160米 D．240米
【答案】B【提示】由题意可知小华走出了一个正多边形，根据正多边形的外角和公式可求解.【详解】已知多边形的外角和为360°，而每一个外角为24°，可得多边形的边数为360°÷24°=15，所以小明一共走了：15×10=150米．故答案选B．
多边形内角和与外角和综合
若一个多边形的外角和与它的内角和相等，则这个多边形是（ ）A．三角形B．四边形 C．五边形D．六边形
【答案】B【提示】任意多边形的外角和为360°，然后利用多边形的内角和公式计算即可．【详解】解：设多边形的边数为n．根据题意得：（n-2）×180°=360°，解得：n=4．故选：B．
【答案】B【提示】多边形的内角和比外角和的3倍多180°，而多边形的外角和是360°，则内角和是3×360°+180°．n边形的内角和可以表示成（n-2）•180°，设这个多边形的边数是n，得到方程，从而求出边数．【详解】根据题意，得：（n-2）•180°=3×360°+180°，解得：n=9，则这个多边形的边数是9．故选B．
用若干个某种正多边形瓷砖可以铺满地面，这种正多边形瓷砖不可能是（ ）
【解析】A、正六边形的每个内角是120°，正方形的每个内角是90°，120m+90n=360°，显然n取任何正整数时，m不能得正整数，故不能铺满；B、正五边形每个内角是180°-360°÷5=108°，正八边形每个内角为135度，135m+108n=360°，显然n取任何正整数时，m不能得正整数，故不能铺满；C、正方形的每个内角为90°，正八边形的每个内角为135°，两个正八边形和一个正方形刚好能铺满地面；D、正三角形每个内角为60度，正十边形每个内角为144度，60m+144n=360°，显然n取任何正整数时，m不能得正整数，故不能铺满．故选C．
能够铺满地面的正多边形组合是（ ）A．正六边形和正方形B．正五边形和正八边形C．正方形和正八边形D．正三角形和正十边形
能够利用多种方法证明多边形外角和
利用多边形外角和解决实际问题