



苏科版七年级下册12.2 证明教学ppt课件
展开判断一件事情的句子叫做命题。
2、证明与图形关的命题的一般步骤是什么?
(1)根据题意,画出图形;
(2)根据命题的条件、结论,结合图形,写出已知、求证;
证明:∵ AB∥CD(已知), ∴ ∠2=∠3(两直线平行,同位角相等) ∵ ∠1+∠3=180°(平角的定义), ∴ ∠1+∠2=180°(等量代换).
证明:两直线平行,同旁内角互补.
已知:AB∥CD.求证:∠1 + ∠2 = 180°.
思考:在这个命题的证明过程中运用了哪些知识?
思考:三角形的三个内角,它们有怎样的数量关系呢?
三个内角的和等于180º.
以前我们是怎么发现这个结论的?
剪拼的方法只是直观感受,度量的方法存在误差,都不能作为证明的依据.
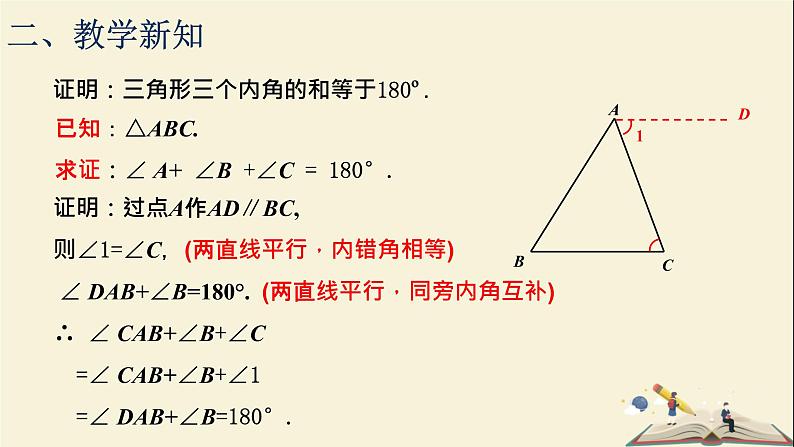
证明:三角形三个内角的和等于180º.
证明:过点A作AD∥BC,则∠1=∠C,(两直线平行,内错角相等) ∠ DAB+∠B=180°. (两直线平行,同旁内角互补)∴ ∠ CAB+∠B+∠C =∠ CAB+∠B+∠1 =∠ DAB+∠B=180°.
已知:△ABC.求证:∠ A+ ∠B +∠C = 180°.
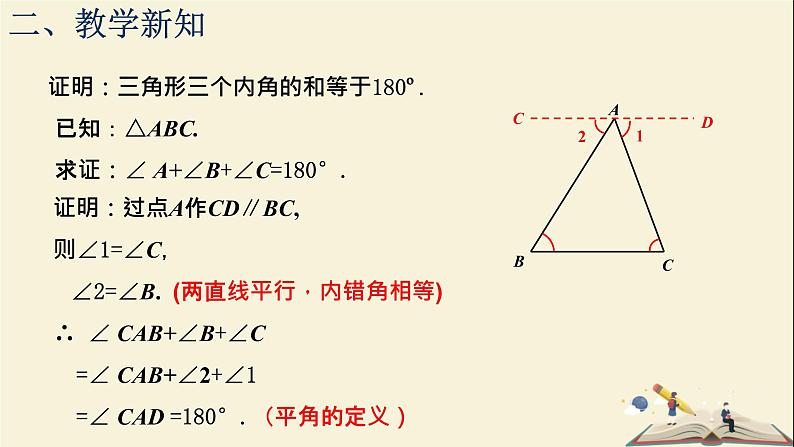
证明:过点A作CD∥BC,则∠1=∠C, ∠2=∠B. (两直线平行,内错角相等)∴ ∠ CAB+∠B+∠C =∠ CAB+∠2+∠1 =∠ CAD =180°.(平角的定义)
已知:△ABC.求证:∠ A+∠B+∠C=180°.
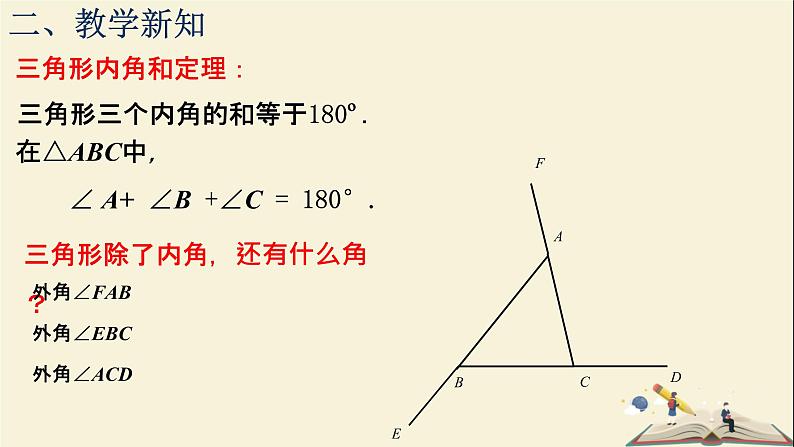
三角形三个内角的和等于180º.
在△ABC中, ∠ A+ ∠B +∠C = 180°.
三角形除了内角,还有什么角?
思考: ∠ACD是△ABC的一个外角,那么它与不相邻的两个内角∠A、∠B之间有怎样的数量关系?为什么?
∵ ∠A+∠B+∠ACB=180° (三角形内角和定理 ) ∠ACD+∠ACB=180° ( 邻补角的定义 )∴ ∠A+∠B=∠ACD.
三角形的一个外角,等于和它与不相邻的两个内角的和.
三角形内角和定理的推论:
三角形的一个外角,等于和它不相邻的两个内角的和.
在△ABC中,∠ACD=∠A+∠B .
已知:如图,AC、BD 相交于点O .
求证:∠A+∠B= ∠C+∠D.
证明:∵ ∠A+∠B+∠AOB=180°(三角形内角和定理) ∠C+∠D+∠COD=180°(三角形内角和定理) ∴ ∠A+∠B+∠AOB= ∠C+∠D+∠COD.(等量代换)∵ ∠AOB= ∠COD, (对顶角相等)∴ ∠A+∠B= ∠C+∠D. (等式性质)
证明:∵在△ABO中,∠A+∠B=∠AOD (三角形的外角等于和它不相邻的两个内角的和) 在△CDO中, ∠C+∠D=∠AOD (三角形的外角等于和它不相邻的两个内角的和) ∴ ∠A+∠B= ∠C+∠D. (等量代换)
4. 已知:如图,AD是△ABC的角平分线,E是BC延长线上一点, ∠B = ∠EAC .求证:∠ADE=∠DAE .
证明:∵ AD是∠ABC的平分线,(已知)∴ ∠1=∠2,(角平分线的定义)∵ ∠B = ∠EAC ,(已知)∴ ∠B+∠1= ∠EAC +∠2,(等式性质)∴ ∠ ADE =∠DAE.
三角形内角的和定理及其推论的应用.
5、已知:如图在△ABC中,∠ABC、 ∠ACB的平分线交于点O,求 ∠BOC与∠A的关系.
初中数学12.2 证明授课ppt课件: 这是一份初中数学12.2 证明授课ppt课件,共33页。PPT课件主要包含了教学目标,知识精讲,情境引入,视觉误差,是静的还是动的,But,证明与定理,等量代换,公理基本事实,前面已证这边可省略等内容,欢迎下载使用。
初中数学苏科版七年级下册12.2 证明课文内容课件ppt: 这是一份初中数学苏科版七年级下册12.2 证明课文内容课件ppt,共12页。PPT课件主要包含了情境引入,活动一考考你的眼力,活动二数学实验室,活动三,活动四,活动五,课堂小结,本节课你有什么收获,课堂作业,拓展延伸等内容,欢迎下载使用。
2021学年12.2 证明评课ppt课件: 这是一份2021学年12.2 证明评课ppt课件,共23页。PPT课件主要包含了眼见为实,实践出真知,眼见未必为实,考考你的眼力,检验你的结论,你的眼睛欺骗你了吗,活动一,活动二,做一做,猜猜看等内容,欢迎下载使用。













