







- 湘教版数学七下:2.2.3运用乘法公式进行计算 课件+教案 课件 25 次下载
- 湘教版数学七下:第2章 整式的乘法 复习课件+教案 课件 31 次下载
- 湘教版数学七下:3.2提公因式法(1) 课件+教案 课件 28 次下载
- 湘教版数学七下:3.2提公因式法(2) 课件+教案 课件 28 次下载
- 湘教版数学七下:3.3公式法(1) 课件+教案 课件 31 次下载
初中数学湘教版七年级下册3.1 多项式的因式分解试讲课ppt课件
展开3.1 多项式的因式分解教案
主备人: 审核人: 本章课时序号:1
课 题 | 多项式的因式分解 | 课型 | 新授课 |
教学目标 | 1. 理解因式分解的概念,了解因式分解的意义。 2. 知道因式分解与整式乘法的联系和区别。 3. 会用多项式的乘法检验因式分解是否正确。 4. 体验类比思想在数学学习中的应用价值。 | ||
教学重点 |
| ||
教学难点 | 1. 识别多项式的等式中的因式分解。 2. 会用多项式的乘法检验因式分解是否正确。 | ||
教 学 活 动 | |||
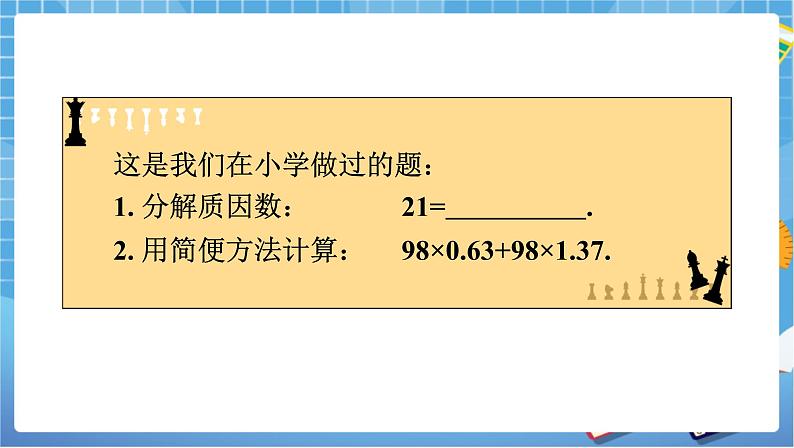
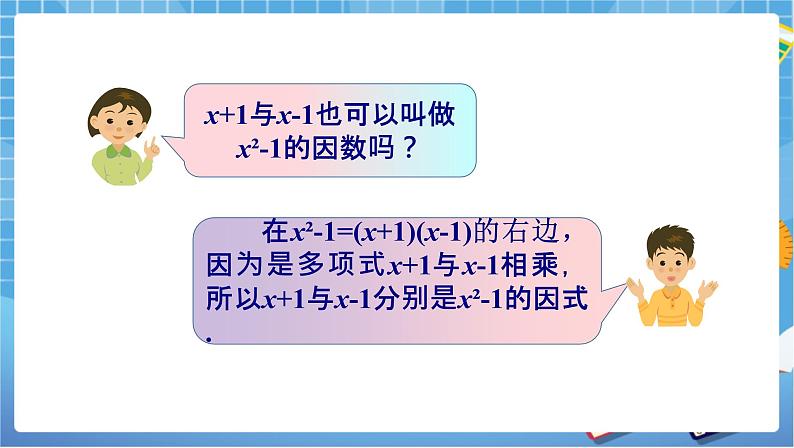
一、情景导入 1、 出示文字,指名朗读:有的时候,我们真的很怀念在小学的美好时光,不由自主地想起在那时学习的情景…… 2、 出示小学经常做的数学题 这是我们在小学做过的题: (1) 分解质因数: 21= . (2) 用简便方法计算: 98×0.63+98×1.37. 3、 展示在小学做这类题的方法 师:你是怎样解答这两道题目的? 生1:对于第1题,我们这样做:因为21等于7乘3,所以21= 7×3 . 生2:对于第2题,把乘法分配律倒过来想: 98×0.63+98×1.37=98×(0.63+1.37)=98×2=196. (设计意图:通过对小学知识的回顾,引导学生用类比的方法理解因式分解的涵义) 二、教学新知 (一) 理解“因式”的概念 1、 x²-1等于x+1乘哪个多项式? (1)启发学生这样想: 1可以看作1²,则x²-1表示x与1的平方差,根据平方差公式x²-1等于什么乘什么? (2)学生回答:因为 (x+1)(x-1)=x²-1,所以 x²-1=(x+1)(x-1). 2、 类比因数的概念得出因式的概念 (1)启发联想:在等式21=3×7中,3和7都叫做21的因数。在等式x²-1=(x+1)(x-1) 中,式子x+1与x-1应该叫做什么? (2)交流讨论: 生1:x+1与x-1也可以叫做x²-1的因数吗? 生2:在x²-1=(x+1)(x-1)的右边,因为是多项式x+1与x-1相乘,所以x+1与x-1分别是x²-1的因式. (3)展示概念: 一般地,对于两个多项式f和g,如果有多项式h使得f=gh,我们把g叫做f的的一 个因式。此时,h也是f的一个因式。 (二) 教学因式分解的概念。 1、 师:把x²-1写成(x+1)(x-1)的形式叫做把这个多项式因式分解。 2、 类比抽象到一般:一般地,把一个多项式表示成若干个多项式的乘积的形式, 称为把这个多项式因式分解。 (设计意图:用分解质因数,通过类比得出因式、分解因式的概念) (三)教学例题1 例1 下列各式由左边到右边的变形,哪些是因式分解,哪些不是,为什么? (1) a2+2ab+b² =(a+b)²; (2) m²+m-4=(m+3)(m-2)+2 . 1、 启发学生根据因式分解的概念进行讨论 2、 教师讲解: (1)是。因为(a+b)²从左边到右边是把多项式a2+2ab+b2表示成a+b与a+b的积的 形式。 (2)不是。因为(m+3)(m-2)+2不是几个多项式的积。3、 阅读第34页“阅读材料” (四)教学例2 例2 检验下列因式分解是否正确。 (1) x²+xy=x(x+y); (2) a²-5a+6=(a-3)(a-2); (3) 4m²-n²=(2m-n)(2m+n) 1、 启发学生根据用多项式的乘法计算等号右边,看是否等于左边。 2、 分组讨论 3、 教师讲解 解 (1)因为x(x+y)=x²+xy,所以因式分解x²+xy=x(x+y)正确。 (2)因为(a-3)(a-2)=a²-5a+6,所以因式分解a²-5a+6=(a-3)(a-2)正确。 (3)因为(2m-n)(2m+n)=4m²-n²,所以因式分解 2m²-n²=(2m-n)(2m+n)正确。 (五)活动:各抒己见 1、 下列从左到右的变形,不是因式分解的是( ) A. x²-xy=x(x-y) B. a²-a-20=(a-5)(a+2) C. m²-2mn+n²=(m-n)² D. (x+y)(x-y)=x²-y² 【答案】D 2、 下列因式分解正确的是( ) A. a²-2ab+a=a(a-2b+1) B. a²-3a-2=(a-3)(a+2) C. m²-2mn+n²=(m+n)2 D. 4x²-y²=(4x+y)(4x-y) 【答案】A (设计意图:通过活动,学生进行充分讨论交流,强化学生对概念的理解) (六)阅读材料,了解因式分解的意义 1、 为将来学习分式的约分化简打下基础 课件展示:类比分数的约分,进行分式的约分过程 2、 类似于用乘法分配律的简便运算,我们可以用简便方法求出某些代数式的值。 例如已知x+y=6,xy=-7,求代入式的值。 可以这样解:x²y+xy²=xy(x+y)=6×(-7)=-42。 3、 因式分解还是今后要学习的解一元二次方程的一种重要方法。 课件展示: 例如4x²-4x+1=0是一个一元二次方程,就可以用因式分解的方法求出它的解。 因此,因式分解是我们今后学习的重要基础。 (设计意图:让学生了解因式分解的重要性,激发学生的求知欲望) 三、课堂练习,固基提能 (一)巩固练习 1、 三个数4,6,14的最大公因数是 . 【答案】2 【思路】先将每个数分解质因数,再找出这些数的公共的因数,求得的积就是最大公因数. 2、 36,60的最大公因数是 . 【答案】12 3、 下列等式从左到右的变形是因式分解的是( ) A. x(x-4y)=x²-4xy B. a²-2a-1=a(a-2)-1 C. (a+b)(a-b)=a²-b² D. x²-2xy+y²=(x-y)² 【答案】D 4、 把下列多项式因式分解,正确的是 ( ) A. a²-3a+2=(a-3)(a-2) B. b²-6b+8=(b-3)² C. m²-2mn+n²=m(m-2n)+n² D. 4x²-8xy=4x(x-2y) (二)能力提升 5、 下列等式从左到右的变形是因式分解的有( ) ① (x+5)(x-1)=x²+4x-5; ② 14ax-14ay=14a(x-y) ③ (m+3)(m-3)=m²-9 ④ x²-10x+25y²=(x-5y)² A. ①② B. ①③ C. ②④ D. ③④ 【答案】C 6、 下列等式从左到右的变形是因式分解的有( ) ① x²-y²-4=(x+y)(x-y)-4; ② a²-2a-1=(a-1)²-3 ③ (m+5n)(m-5n)=m²-25n² ④ x²-2xy+y²=(x-y)² ⑤ 5x²-7x+x=x(5x-7x+1) A. ①②④ B. ①③④ C. ①④⑤ D. ④⑤ 【答案】D 7、 小明在水果店买了苹果、梨、葡萄各akg,这三种水果的单价分别是x,y,z元。小明一共要花多少元? (1)先分别算出买每种水果花多少元,再算一共要花多少元,列成一个代数式是 。 (2)先算三种水果的单价和,再算一共要花多少元,列成一个代数式是 。 (3)根据(1)题和(2)题写出一个关于因式分解的等式是 。 【答案】(1)ax+ay+az (2)a(x+y+z) (3)ax+ay+az=a(x+y+z)
四、课堂总结: 1、 什么叫做因式分解? 2、 因式分解与整式乘法有何关系? 3、 如何检验一个多项式的等式是否为因式分解? | |||
板书设计 |
3.1多项式的因式分解 1、 多项式的因式分解及因式的概念 2、 多项式的因式分解与多项式乘法的联系与区别 3、 用多项式的乘法检验多项式的因式分解 | ||
初中数学3.1 多项式的因式分解教案配套课件ppt: 这是一份初中数学3.1 多项式的因式分解教案配套课件ppt,文件包含31多项式的因式分解pptx、31多项式的因式分解docx、31多项式的因式分解练习doc等3份课件配套教学资源,其中PPT共11页, 欢迎下载使用。
初中数学湘教版七年级下册第3章 因式分解3.1 多项式的因式分解说课课件ppt: 这是一份初中数学湘教版七年级下册第3章 因式分解3.1 多项式的因式分解说课课件ppt,文件包含31多项式的因式分解课件ppt、31多项式的因式分解教案DOCX等2份课件配套教学资源,其中PPT共14页, 欢迎下载使用。
湘教版七年级下册第3章 因式分解3.1 多项式的因式分解多媒体教学课件ppt: 这是一份湘教版七年级下册第3章 因式分解3.1 多项式的因式分解多媒体教学课件ppt,共27页。













