

2020-2021学年广东省茂名市电白区七年级(上)期末数学试卷 解析版
展开
这是一份2020-2021学年广东省茂名市电白区七年级(上)期末数学试卷 解析版,共19页。试卷主要包含了选择题.,填空题,解答题.,解答题等内容,欢迎下载使用。
2020-2021学年广东省茂名市电白区七年级(上)期末数学试卷
一、选择题(每小题3分,共30分).
1.(3分)2016年某市用于资助贫困学生的助学金总额是9680000元,将9680000用科学记数法表示为( )
A.96.8×105 B.9.68×106 C.9.68×107 D.0.968×108
2.(3分)下列调查中,最适宜采用普查方式的是( )
A.对全国初中学生视力状况的调查
B.对“十一国庆”期间全国居民旅游出行方式的调查
C.旅客上飞机前的安全检查
D.了解某种品牌手机电池的使用寿命
3.(3分)如图,由5个完全相同的小正方体组合成一个立体图形,它的左视图是( )
A. B. C. D.
4.(3分)小明做了以下5道题:①0﹣(﹣3)=﹣3;②(﹣3)+(﹣8)=﹣11;③;④(﹣24)÷(﹣6)=﹣4;⑤﹣110=1.请你帮他检查一下,他一共做对了多少道?( )
A.1 B.2 C.3 D.4
5.(3分)点A,B,C在同一直线上,已知AB=3cm,BC=1cm,则线段AC的长是( )
A.2cm B.3cm C.4cm D.2cm或4cm
6.(3分)“某幼儿园给小朋友分苹果,若每个小朋友分3个则剩1个;若每个小朋友分4个则少2个,问苹果有多少个?”若设共有x个苹果,则列出的方程是( )
A.3x+1=4x﹣2 B.3x﹣1=4x+2 C. D.
7.(3分)如图,点A、B、C是直线l上的三个点,图中共有线段条数是( )
A.1条 B.2条 C.3条 D.4条
8.(3分)如图,正方形的边长为a,图中阴影部分的面积可以表示为( )
A. B. C. D.
9.(3分)如图,两块直角三角板的直角顶点O重合在一起,若∠BOC=∠AOD,则∠BOC的度数为( )
A.22.5° B.30° C.45° D.60°
10.(3分)某公司员工分别在A,B,C三个住宅区居住,A区有30人,B区有15人,C区有10人,三个区在同一条直线上,位置如图所示,该公司的接送车打算在此间只设一个停靠点,为使所有员工步行到停靠点的路程之和最小,那么停靠点的位置应设在( )
A.A区 B.B区
C.C区 D.A、B两区之间
二、填空题:(每小题4分,共28分)
11.(4分)的系数为 ,次数为 .
12.(4分)某正方体的每个面上都有一个汉字,如图是它的一个展开图,则在原正方体中,与“想”字所在面相对的面上的汉字是 .
13.(4分)钟表在4点半时,它的时针与分针所成锐角是 度.
14.(4分)已知代数式2a3bn+1与﹣3am﹣2b2是同类项,则2m+3n= .
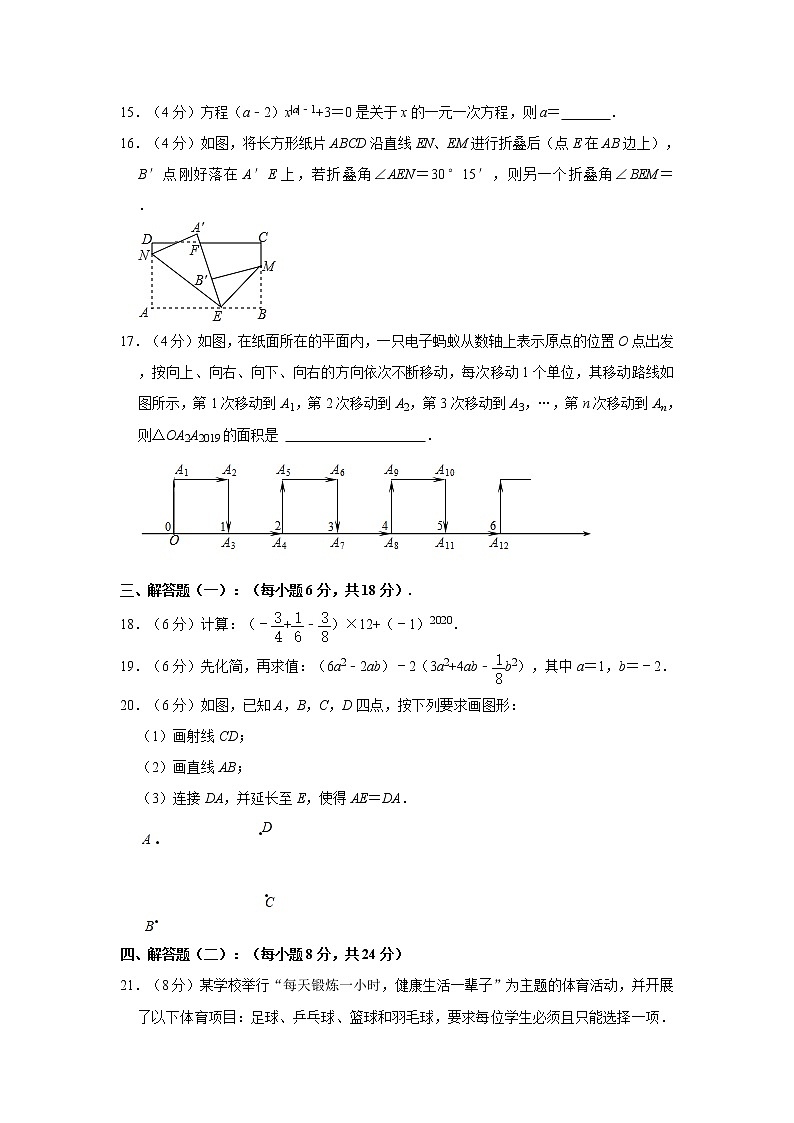
15.(4分)方程(a﹣2)x|a|﹣1+3=0是关于x的一元一次方程,则a= .
16.(4分)如图,将长方形纸片ABCD沿直线EN、EM进行折叠后(点E在AB边上),B′点刚好落在A′E上,若折叠角∠AEN=30°15′,则另一个折叠角∠BEM= .
17.(4分)如图,在纸面所在的平面内,一只电子蚂蚁从数轴上表示原点的位置O点出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其移动路线如图所示,第1次移动到A1,第2次移动到A2,第3次移动到A3,…,第n次移动到An,则△OA2A2019的面积是 .
三、解答题(一):(每小题6分,共18分).
18.(6分)计算:(﹣+﹣)×12+(﹣1)2020.
19.(6分)先化简,再求值:(6a2﹣2ab)﹣2(3a2+4ab﹣b2),其中a=1,b=﹣2.
20.(6分)如图,已知A,B,C,D四点,按下列要求画图形:
(1)画射线CD;
(2)画直线AB;
(3)连接DA,并延长至E,使得AE=DA.
四、解答题(二):(每小题8分,共24分)
21.(8分)某学校举行“每天锻炼一小时,健康生活一辈子”为主题的体育活动,并开展了以下体育项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择一项.为了解选择各项体育活动的学生人数,随机抽取了部分学生进行调查,并将获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据统计图回答问题:
(1)这次活动一共调查了 名学生;
(2)补全条形统计图;
(3)求选择篮球项目的人数在扇形统计图中所占的百分比?
(4)若该学校有1500人,请你估计该学校选择乒乓球项目的学生人数约是多少人?
22.(8分)如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)求出∠BOD的度数;
(2)请通过计算说明OE是否平分∠BOC.
23.(8分)某中学学生步行到郊外旅行.七年级(1)班学生组成前队,步行速度为4千米/时,七(2)班的学生组成后队,速度为6千米/时;前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回联络,他骑车的速度为10千米/时.
(1)后队追上前队需要多长时间?
(2)后队追上前队时间内,联络员走的路程是多少?
(3)两队何时相距2千米?
五、解答题(三):(每小题10分,共20分)
24.(10分)某社区超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲
乙
进价(元/件)
22
30
售价(元/件)
29
40
(1)该超市购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元,求第二次乙商品是按原价打几折销售?
25.(10分)已知数轴上三点A、O、B表示的数分别为4、0、﹣2,动点P从A点出发,以每秒3个单位的速度沿数轴向左匀速运动.
(1)当点P到点A的距离与点P到点B的距离相等时,点P在数轴上表示的数是 .
(2)另一动点R从点B出发,以每秒2个单位的速度沿数轴向左匀速运动,若点P、R同时出发,问点P运动多长时间追上点R?
(3)若点M为AP的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若发生变化,请你说明理由;若不变,请你画出图形,并求出线段MN的长度.
2020-2021学年广东省茂名市电白区七年级(上)期末数学试卷
参考答案与试题解析
一、选择题(每小题3分,共30分).
1.(3分)2016年某市用于资助贫困学生的助学金总额是9680000元,将9680000用科学记数法表示为( )
A.96.8×105 B.9.68×106 C.9.68×107 D.0.968×108
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥1时,n是非负数;当原数的绝对值<1时,n是负数.
【解答】解:将9680000用科学记数法表示为:9.68×106.
故选:B.
2.(3分)下列调查中,最适宜采用普查方式的是( )
A.对全国初中学生视力状况的调查
B.对“十一国庆”期间全国居民旅游出行方式的调查
C.旅客上飞机前的安全检查
D.了解某种品牌手机电池的使用寿命
【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
【解答】解:A、对全国初中学生视力状况的调查,范围广,适合抽样调查,故A错误;
B、对“十一国庆”期间全国居民旅游出行方式的调查范围广,适合抽样调查,故B错误;
C、旅客上飞机前的安全检查,适合普查,故C正确;
D、了解某种品牌手机电池的使用寿命,适合抽样调查,故D错误;
故选:C.
3.(3分)如图,由5个完全相同的小正方体组合成一个立体图形,它的左视图是( )
A. B. C. D.
【分析】找到从左面看所得到的图形即可,注意所有的看到的棱都应表现在左视图中.
【解答】解:从左面看易得第一层有2个正方形,第二层最左边有一个正方形.
故选:B.
4.(3分)小明做了以下5道题:①0﹣(﹣3)=﹣3;②(﹣3)+(﹣8)=﹣11;③;④(﹣24)÷(﹣6)=﹣4;⑤﹣110=1.请你帮他检查一下,他一共做对了多少道?( )
A.1 B.2 C.3 D.4
【分析】根据有理数的运算法则计算得到结果,即可作出判断.
【解答】解:①0﹣(﹣3)=3,原计算错误;
②(﹣3)+(﹣8)=﹣11,原计算正确;
③×(﹣)=﹣,原计算正确;
④(﹣24)÷(﹣6)=4,原计算错误;
⑤﹣110=﹣1,原计算错误.
则他一共做对了2题,
故选:B.
5.(3分)点A,B,C在同一直线上,已知AB=3cm,BC=1cm,则线段AC的长是( )
A.2cm B.3cm C.4cm D.2cm或4cm
【分析】本题没有给出图形,在画图时,应考虑到A、B、C三点之间的位置关系的多种可能,再根据题意画出的图形进行解答.
【解答】解:本题有两种情形:
(1)当点C在线段AB上时,如图,AC=AB﹣BC,
又∵AB=3cm,BC=1cm,
∴AC=3﹣1=2cm;
(2)当点C在线段AB的延长线上时,如图,AC=AB+BC,
又∵AB=3cm,BC=1cm,
∴AC=3+1=4cm.
故线段AC=2cm或4cm.
故选:D.
6.(3分)“某幼儿园给小朋友分苹果,若每个小朋友分3个则剩1个;若每个小朋友分4个则少2个,问苹果有多少个?”若设共有x个苹果,则列出的方程是( )
A.3x+1=4x﹣2 B.3x﹣1=4x+2 C. D.
【分析】根据苹果总个数不变,结合每个小朋友分3个则剩1个;每个小朋友分4个则少2个,分别表示苹果数量进而得出等式即可.
【解答】解:∵设共有x个苹果,
∴每个小朋友分3个则剩1个时,小朋友的人数是:,
若每个小朋友分4个则少2个时,小朋友的人数是:,
∴,
故选:C.
7.(3分)如图,点A、B、C是直线l上的三个点,图中共有线段条数是( )
A.1条 B.2条 C.3条 D.4条
【分析】写出所有的线段,然后再计算条数.
【解答】解:图中线段有:线段AB、线段AC、线段BC,共三条.
故选:C.
8.(3分)如图,正方形的边长为a,图中阴影部分的面积可以表示为( )
A. B. C. D.
【分析】阴影部分的面积=×以a为半径圆的面积﹣×以a为半径圆的面积.
【解答】解:根据题意知,阴影部分的面积=×πa2﹣×π×(a)2=.
故选:D.
9.(3分)如图,两块直角三角板的直角顶点O重合在一起,若∠BOC=∠AOD,则∠BOC的度数为( )
A.22.5° B.30° C.45° D.60°
【分析】此题由“两块直角三角板”可知∠DOC=∠BOA=90°,根据同角的余角相等可以证明∠DOB=∠AOC,由题意设∠BOC=x°,则∠AOD=7x°,结合图形列方程即可求解.
【解答】解:由两块直角三角板的直顶角O重合在一起可知:∠DOC=∠BOA=90°,
∴∠DOB+∠BOC=90°,∠AOC+∠BOC=90°,
∴∠DOB=∠AOC,
设∠BOC=x°,则∠AOD=7x°,
∴∠DOB+∠AOC=∠AOD﹣∠BOC=6x°,
∴∠DOB=3x°,
∴∠DOB+∠BOC=4x°=90°,
解得:x=22.5.
故选:A.
10.(3分)某公司员工分别在A,B,C三个住宅区居住,A区有30人,B区有15人,C区有10人,三个区在同一条直线上,位置如图所示,该公司的接送车打算在此间只设一个停靠点,为使所有员工步行到停靠点的路程之和最小,那么停靠点的位置应设在( )
A.A区 B.B区
C.C区 D.A、B两区之间
【分析】根据题意分别计算停靠点分别在A、B、C各点和A区、B区之间时员工步行的路程和,选择最小的值即可求解.
【解答】解:∵当停靠点在A区时,所有员工步行到停靠点路程和是:
15×100+10×300=4500(m),
当停靠点在B区时,所有员工步行到停靠点路程和是:30×100+10×200=5000(m ),
当停靠点在C区时,所有员工步行到停靠点路程和是:30×300+15×200=12000(m ),
当停靠点在A、B区之间时,
设在A区、B区之间时,设距离A区x米,
则所有员工步行路程之和=30x+15( 100﹣x)+10 ( 100+200﹣x)
=30x+1500﹣15x+3000﹣10x
=5x+4500,
∴当x=0时,即在A区时,路程之和最小,为4500米,
综上,当停靠点在A区时,所有员工步行到停靠点路程和最小,
故选:A.
二、填空题:(每小题4分,共28分)
11.(4分)的系数为 ﹣ ,次数为 3 .
【分析】单项式中的数字因数叫做单项式的系数,一个单项式中所有字母的指数的和叫做单项式的次数.
【解答】解:的系数为﹣,次数为3.
故答案为:﹣,3.
12.(4分)某正方体的每个面上都有一个汉字,如图是它的一个展开图,则在原正方体中,与“想”字所在面相对的面上的汉字是 亮 .
【分析】利用正方体及其表面展开图的特点解题.
【解答】解:这是一个正方体的平面展开图,共有六个面,与“想”字所在面相对的面上的汉字是亮.
故答案为:亮.
13.(4分)钟表在4点半时,它的时针与分针所成锐角是 45 度.
【分析】根据钟面平均分成12份,可得每份的度数,根据时针与分针相距的份数乘以每份的度数,可得答案.
【解答】解:钟表在4点半时,它的时针与分针所成锐角是30°×1.5=45°.
故答案为:45.
14.(4分)已知代数式2a3bn+1与﹣3am﹣2b2是同类项,则2m+3n= 13 .
【分析】本题考查同类项的定义(所含字母相同,相同字母的指数相同),可得:m﹣2=3,n+1=2,解方程即可求得m,n的值,从而求出2m+3n的值.
【解答】解:由同类项的定义,
可知m﹣2=3,n+1=2,
解得n=1,m=5,
则2m+3n=13.
故答案为:13
15.(4分)方程(a﹣2)x|a|﹣1+3=0是关于x的一元一次方程,则a= ﹣2 .
【分析】只含有一个未知数(元),并且未知数的指数是1(次)的方程叫做一元一次方程,它的一般形式是ax+b=0(a,b是常数且a≠0).
【解答】解:由一元一次方程的特点得:|a|﹣1=1,a﹣2≠0,
解得:a=﹣2.
故答案为:﹣2.
16.(4分)如图,将长方形纸片ABCD沿直线EN、EM进行折叠后(点E在AB边上),B′点刚好落在A′E上,若折叠角∠AEN=30°15′,则另一个折叠角∠BEM= 59°45′ .
【分析】由折叠性质得∠AEN=∠A′EN,∠BEM=∠B′EM,即可得出结果;
【解答】解:由折叠性质得:∠AEN=∠A′EN,∠BEM=∠B′EM,
∴∠A′EN=30°15′,
∠BEM=(180°﹣∠AEN﹣∠A′EN)=(180°﹣30°15′﹣30°15′)=59°45′,
故答案为:59°45′.
17.(4分)如图,在纸面所在的平面内,一只电子蚂蚁从数轴上表示原点的位置O点出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其移动路线如图所示,第1次移动到A1,第2次移动到A2,第3次移动到A3,…,第n次移动到An,则△OA2A2019的面积是 .
【分析】观察图形可知:OA4n=2n,由OA2016=1008,推出OA2019=1009,由此即可解决问题.
【解答】解:观察图形可知:点A4n在数轴上,OA4n=2n,
∵OA2016=1008,
∴OA2019=1009,点A2019在数轴上,
∴S=×1009×1=,
故答案为:.
三、解答题(一):(每小题6分,共18分).
18.(6分)计算:(﹣+﹣)×12+(﹣1)2020.
【分析】原式利用乘法分配律及乘方的意义计算,即可得到结果.
【解答】解:原式=﹣×12+×12﹣×12+1
=﹣9+2﹣+1
=﹣.
19.(6分)先化简,再求值:(6a2﹣2ab)﹣2(3a2+4ab﹣b2),其中a=1,b=﹣2.
【分析】先去括号,再合并同类项,最后代入求值.
【解答】解:原式=6a2﹣2ab﹣6a2﹣8ab+b2
=﹣10ab+b2,
当a=1,b=﹣2时,
原式=﹣10×1×(﹣2)+×(﹣2)2
=20+1
=21.
20.(6分)如图,已知A,B,C,D四点,按下列要求画图形:
(1)画射线CD;
(2)画直线AB;
(3)连接DA,并延长至E,使得AE=DA.
【分析】(1)画射线CD即可;
(2)画直线AB即可;
(3)连接DA,并延长至E,使得AE=DA即可.
【解答】解:如图所示,
(1)射线CD即为所求作的图形;
(2)直线AB即为所求作的图形;
(3)连接DA,并延长至E,使得AE=DA.
四、解答题(二):(每小题8分,共24分)
21.(8分)某学校举行“每天锻炼一小时,健康生活一辈子”为主题的体育活动,并开展了以下体育项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择一项.为了解选择各项体育活动的学生人数,随机抽取了部分学生进行调查,并将获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据统计图回答问题:
(1)这次活动一共调查了 250 名学生;
(2)补全条形统计图;
(3)求选择篮球项目的人数在扇形统计图中所占的百分比?
(4)若该学校有1500人,请你估计该学校选择乒乓球项目的学生人数约是多少人?
【分析】(1)根据选择足球的人数和所占的百分比可以求得本次调查的人数;
(2)根据(1)中的结果和条形统计图中的数据可以计算出选择篮球的人数,从而可以将条形统计图补充完整;
(3)根据统计图中的数据可以计算出选择篮球项目的人数在扇形统计图中所占的百分比;
(4)根据统计图中的数据可以计算出该学校选择乒乓球项目的学生人数约是多少人.
【解答】解:(1)这次活动一共调查了:80÷32%=250(名)学生,
故答案为:250;
(2)选择篮球的有:250﹣80﹣40﹣60=70(人),
补全的条形统计图如右图所示;
(3)×100%=28%,
答:选择篮球项目的人数在扇形统计图中占28%;
(4)(人),
答:该学校选择乒乓球项目的学生人数约是240人.
22.(8分)如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)求出∠BOD的度数;
(2)请通过计算说明OE是否平分∠BOC.
【分析】(1)根据∠BOD=∠DOC+∠BOC,首先利用角平分线的定义和邻补角的定义求得∠DOC和∠BOC即可;
(2)根据∠DOC与∠COE互余即可得出∠COE的度数,由(1)可知∠BOC=130°,那么∠BOE=∠BOC﹣∠COE=65°,进而可得出结论,从而求解.
【解答】解:(1)因为∠AOC=50°,OD平分∠AOC,
所以∠DOC=∠AOC=25°,∠BOC=180°﹣∠AOC=130°,
所以∠BOD=∠DOC+∠BOC=155°;
(2)OE平分∠BOC.理由如下:
∵∠DOE=90°,∠DOC=25°,
∴∠COE=90°﹣25°=65°,
∵∠BOC=130°,
∴∠BOE=∠BOC﹣∠COE=130°﹣65°=65°,
∴∠COE=∠BOE,
∴OE平分∠BOC.
23.(8分)某中学学生步行到郊外旅行.七年级(1)班学生组成前队,步行速度为4千米/时,七(2)班的学生组成后队,速度为6千米/时;前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回联络,他骑车的速度为10千米/时.
(1)后队追上前队需要多长时间?
(2)后队追上前队时间内,联络员走的路程是多少?
(3)两队何时相距2千米?
【分析】(1)设后队追上前队需要x小时,根据后队比前队快的速度×时间=前队比后队先走的路程可列出方程,解出即可得出时间;
(2)先计算出联络员所走的时间,再由路程=速度×时间即可得出联络员走的路程.
(3)要分三种情况讨论:①当(1)班出发半小时后,相距2千米;②当(2)班还没有超过(1)班时,相距2千米;③当(2)班超过(1)班后,(1)班与(2)班再次相距2千米,分别列出方程,求解即可.
【解答】解:(1)设后队追上前队需要x小时,
由题意得:(6﹣4)x=4×1,
解得:x=2.
故后队追上前队需要2小时;
(2)后队追上前队时间内,联络员走的路程就是在这2小时内所走的路,
所以10×2=20(千米).
答:后队追上前队时间内,联络员走的路程是20千米;
(3)要分三种情况讨论:
①当七年级(1)班出发半小时后,两队相距4×=2(千米)
②当七年级(2)班还没有超过(1)班时,相距2千米,
设七年级(2)班需y小时与七年级(1)相距2千米,
由题意得:(6﹣4)y=2,
解得:y=1;
所以当七年级(2)班出发1小时后两队相距2千米;
③当七年级(2)班超过七年级(1)班后,七年级(1)班与七年级(2)班再次相距2千米时
(6﹣4)y=4+2,
解得:y=3.
答当七年级(1)班出发0.5小时或当七年级(2)班出发1小时后或3小时后,两队相距2千米.
五、解答题(三):(每小题10分,共20分)
24.(10分)某社区超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲
乙
进价(元/件)
22
30
售价(元/件)
29
40
(1)该超市购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元,求第二次乙商品是按原价打几折销售?
【分析】(1)设第一次购进甲种商品x件,则购进乙种商品(x+15)件,根据单价×数量=总价,即可得出关于x的一元一次方程,解之即可得出结论;
(2)根据总利润=单件利润×销售数量,列式计算即可求出结论;
(3)设第二次乙种商品是按原价打y折销售,根据总利润=单件利润×销售数量,即可得出关于y的一元一次方程,解之即可得出结论.
【解答】解:(1)设第一次购进甲种商品x件,则购进乙种商品(x+15)件,
根据题意得:22x+30(x+15)=6000,
解得:x=150,
∴x+15=90.
答:该超市第一次购进甲种商品150件、乙种商品90件.
(2)(29﹣22)×150+(40﹣30)×90=1950(元).
答:该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得利润1950元.
(3)设第二次乙种商品是按原价打y折销售,
根据题意得:(29﹣22)×150+(40×﹣30)×90×3=1950+180,
解得:y=8.5.
答:第二次乙商品是按原价打8.5折销售.
25.(10分)已知数轴上三点A、O、B表示的数分别为4、0、﹣2,动点P从A点出发,以每秒3个单位的速度沿数轴向左匀速运动.
(1)当点P到点A的距离与点P到点B的距离相等时,点P在数轴上表示的数是 1 .
(2)另一动点R从点B出发,以每秒2个单位的速度沿数轴向左匀速运动,若点P、R同时出发,问点P运动多长时间追上点R?
(3)若点M为AP的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若发生变化,请你说明理由;若不变,请你画出图形,并求出线段MN的长度.
【分析】(1)由已知条件得到AB=6,由PA=PB,于是得到结论;
(2)设点P运动x秒时,在点C处追上点R,于是得到AC=3x BC=2x,AB=6,根据AC=BC+AB,列方程即可得到结论;
(3)线段MN的长度不发生变化,理由如下分两种情况:①当点P在A、B之间运动时,②当点P运动到点B左侧时,求得线段MN的长度不发生变化.
【解答】解:(1)∵A,B表示的数分别为4,﹣2,
∴AB=6,
∵PA=PB,
∴点P表示的数是1,
故答案为:1;
(2)设P点运动x秒追上R点,由题意得:2x+6=3x
解得:x=6
答:P点运动6秒追上R点.
(3)MN的长度不变.
①当P点在线段AB上时,如图示:
∵M为PA的中点,N为PB的中点
∴
又∵MN=MP+NP
∴
∵AP+BP=AB,AB=6
∴
②当P点在线段AB的延长线上时,如图示:
∵MN=MP﹣NP,AB=AP﹣BP=6
∴=.
相关试卷
这是一份2022-2023学年广东省茂名市电白区七年级(下)期末数学试卷(含解析),共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2022-2023学年广东省茂名市电白区七年级(下)期末数学试卷(含解析),共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2022-2023学年广东省茂名市电白区八年级(下)期末数学试卷(含解析),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。









