北师大版 (2019)必修 第二册6.1 余弦定理与正弦定理教学ppt课件

这是一份北师大版 (2019)必修 第二册6.1 余弦定理与正弦定理教学ppt课件，共50页。PPT课件主要包含了课标阐释，思维脉络，激趣诱思，知识点拨，探究一，探究二，当堂检测，角度2证明问题，答案B，答案D等内容，欢迎下载使用。

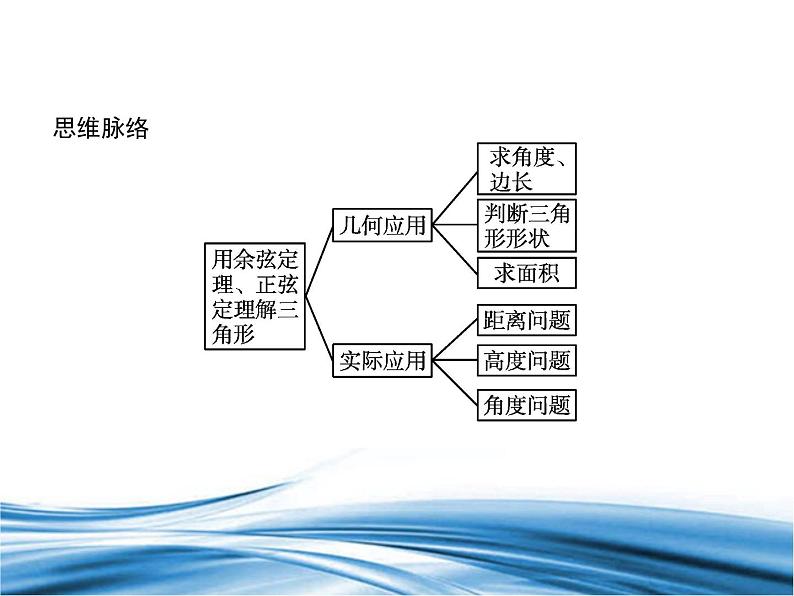
1.会用正弦定理、余弦定理解决与三角形有关的几何计算问题.(数学运算、逻辑推理)2.会用正弦定理、余弦定理解决与距离、高度、角度有关的实际问题.(数学建模、数学运算)
滑行的距离滑冰是一项集力量、耐力和速度于一身的运动项目.在第21届温哥华冬奥会上,有两个滑冰者甲和乙位于冰面上A、B两点,A与B相距100 m.如果甲从A出发,以8 m/s速度沿着一条与AB成60°角的直线滑行,同时乙从B出发,以7 m/s 的速度沿着与甲相遇的最短直线滑行.那么相遇时,甲滑行了多远呢?
一、解三角形与三角形有关的几何计算在三角形的三条边和三个角这6个元素中,如果已知3个(至少含一边长),那么由余弦定理和正弦定理,就可以求得其他3个元素.具体情形如下:情形1　已知两个角的大小与一条边的边长.先由三角形内角和等于180°求出第三个角的大小,然后依据正弦定理求得另外两条边的边长.情形2　已知两条边的边长及其夹角的大小.先由余弦定理求出第三条边的边长,然后再由余弦定理求得第二、第三个角的大小.
情形3　已知三条边的边长.由余弦定理求出两个角,再利用三角形内角和等于180°求出第三个角.情形4　已知两条边的边长和其中一边对角的大小.首先,由正弦定理求出第二条边所对角的正弦,这时,要判断是两解、一解还是无解.然后,根据三角形内角和等于180°得到第三个角的大小.最后,由余弦定理或正弦定理求得第三条边的边长.
名师点析1.应用正弦定理可以解决怎样的解三角形问题?(1)已知三角形的任意两个角与一边,求其他两边和另一角.(2)已知三角形的两边与其中一边的对角,求另一边的对角,进而计算出其他的边和角.2.应用余弦定理可以解决哪些解三角形问题?(1)已知三角形的两边及其夹角,求其他的边和角.(2)已知三角形的三边,求三个角.
答案(1)C　(2)等腰直角三角形
二、解三角形的实际应用1.实际测量中的有关名称、术语
2.解三角形应用题的步骤解三角形应用题时,通常都要根据题意,从实际问题中抽象出一个或几个三角形,然后通过解三角形,得到实际问题的解.求解的关键是将实际问题转化为解三角形问题.
(1)解题思路(2)基本步骤①分析:理解题意,弄清已知与未知,画出示意图(一个或几个三角形);②建模:根据已知条件与求解目标,把已知量与待求量尽可能地集中在有关三角形中,建立一个解三角形的数学模型;③求解:利用正弦定理、余弦定理解三角形,求得数学模型的解;④检验:检验所求的解是否符合实际问题,从而得出实际问题的解.
微思考张晓同学从家中出发,先向东走了1 000 m,然后拐弯向北走了200 m,你能用什么方法确定其方位?答案方向角
微练习1从A处望B处的仰角为α,从B处望A处的俯角为β,则α,β的关系是(　　)A.α>β　　　　　B.α=β C.α+β=90°D.α+β=180°解析如图,在A处望B处的仰角α与从B处望A处的俯角β是内错角,根据水平线平行,得α=β.答案B
微练习2已知目标A的方位角为135°,请画出其图示.解如图所示:
微练习3请分别画出北偏东30°,南偏东45°的方向角.解如图所示:
解三角形与三角形有关的几何计算角度1　三角形中线段长度的计算例1在四边形ABCD中,已知AD⊥CD,AD=10,AB=14,∠BDA=60°,∠BCD=135°,求BC的长.
解在△ABD中,设BD=x,由余弦定理,得BA2=BD2+AD2-2BD·AD·cs∠BDA即142=x2+102-2·10x·cs 60°,整理得x2-10x-96=0,解得x1=16,x2=-6(舍去),所以BD=16.由AD⊥CD,∠BDA=60°,知∠CDB=30°,
反思感悟 解决此类问题要处理好两个关键点(1)找出已知某边长的三角形,从中筛选出可解三角形.(2)找要求线段所在的三角形,确定所需条件.解题时二者应结合,明确解题思路.
反思感悟 解决此类问题时,要灵活运用三角形中特有的恒等变形公式、三角形边和角的相互转换公式,主要是正弦定理、余弦定理,因此这类题型都可用不同的途径求解.
解三角形的实际应用角度1　测量距离问题§1　求可到达点与不可到达点之间的距离问题例3如图 ,一名学生在河岸紧靠岸边笔直行走,开始在A处,经观察,在河的对岸有一参照物C,与学生前进方向成30°角,学生前进200 m 后到达点B,测得该参照物与前进方向成75°角.(1)求点A与参照物C的距离;(2)求河的宽度.
反思感悟 1.测量从一个可到达的点与一个不可到达的点之间的距离问题,一般可转化为已知两个角和一条边解三角形的问题,从而运用正弦定理解决.2.如图,点B为不可到达点,求A,B的距离的具体解题步骤:(1)取基线AC(尽量长),且使AB,AC不共线;(2)测量AC,∠BAC,∠BCA;
变式训练3 如图所示,为了测量河的宽度,在一岸边选定两点A,B,望对岸标记物C,测得∠CAB=30°,∠CBA=75°,AB=120 m,则河的宽度为　　　m. 
解析由题意,得∠ACB=180°-30°-75°=75°,所以△ABC为等腰三角形.因为河宽即边AB上的高,这与边AC上的高相等,过点B作BD⊥AC于D,所以河宽=BD=120sin 30°=60(m).答案60
反思感悟 测量两个不可到达的点之间的距离问题,一般是先把求距离问题转化为应用余弦定理求三角形的边长的问题,再把求未知的边长问题转化为只有一点不能到达的两点距离测量问题,最后运用正弦定理解决问题.
(1)A处与D处的距离;(2)灯塔C与D处的距离.
角度2　测量高度问题例5如图,为了测量河对岸的塔高AB,选取与塔底B在同一水平面内的两个测点C和D,测得CD=200 m,在点C和点D测得塔顶A的仰角分别是45°和30°,且∠CBD=30°,求塔高AB.
反思感悟 1.在测量底部不可到达的建筑物的高度时,可以借助正弦定理或余弦定理,构造两角(两个仰角或两个俯角)和一边或三角(两个方向角和仰角)和一边,如图所示.
2.解决测量高度问题的一般步骤:
变式训练5如图,在山顶铁塔上B处测得一点A的俯角为α,在塔底C处测得A处的俯角为β.若铁塔高为m米,则山高CD为　　　　　米. 
因为AB=40 m,所以AB=PB,所以∠APB=∠PAB=30°,所以∠PBA=120°.因此测绘人员到达点B时,目标参照物P相对于该测绘人员的方位角为180°-120°=60°,且目标参照物P与他的距离为40 m.
反思感悟 解决实际测量中的角度问题的基本步骤(1)找准观测点以及参照物,根据“上北下南,左西右东”确定正北方向;(2)根据题意作出示意图;(3)分析图中的已知量和未知量,标出有关角和线段的大小;(4)利用正弦定理或余弦定理解三角形,求出未知量.
变式训练6如图所示,从A到B,方位角是50°,距离是470 m;从B到C,方位角是80°,距离是860 m;从C到D,方位角是150°,距离是640 m,试计算从A到D的方位角和距离.
§2　航海与追击中的角度问题例7某渔轮在航行中不幸遇险,发出呼救信号,我海军舰艇在A处获悉后,立即测出该渔轮在方位角为45°,距离为10 n mile的C处,并测得渔轮正沿方位角为105°的方向,以9 n mile/h的速度向某小岛靠拢,我海军舰艇立即以21 n mile/h的速度前去营救,求舰艇的航向和靠近渔轮所需的时间.
反思感悟 1.本题欲求方位角,先求边长,而要求边长,需先求时间.由于舰艇与渔轮同时在移动,因此相遇点不确定,即舰艇的航向不确定,解题时画图的关键是设出相遇点B,画出可以求解的三角形.2.解决这类问题,首先明确题中所给各个角的含义,然后分析题意,根据题意画出正确的示意图,将实际问题转化为数学问题,运用正弦定理或余弦定理求解.
1.如果等腰三角形的周长是底边长的5倍,则它的顶角的余弦值为(　　)
2.若P在Q的北偏东44°50'方向上,则Q在P的(　　)A.东偏北45°10'方向上B.北偏东45°50'方向上C.南偏西44°50'方向上D.西偏南45°50'方向上解析如图所示,点Q在点P的南偏西44°50'方向上.答案C