2021-2022学年山东省济宁市鱼台县八年级（上）期中数学试卷 解析版

这是一份2021-2022学年山东省济宁市鱼台县八年级（上）期中数学试卷 解析版，共19页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。
2021-2022学年山东省济宁市鱼台县八年级（上）期中数学试卷
一、选择题：（共10小题每小题3分共30分下面每小题只有一选项是正确的，请将正确选项涂在答题卡上
1．（3分）点M（﹣2，3）关于x轴对称点的坐标为（　　）
A．（﹣2，﹣3） B．（2，﹣3） C．（﹣3，﹣2） D．（2，3）
2．（3分）下面三根木条能组成三角形的是（　　）
A．1cm，2cm，5cm B．2cm，2cm，4cm
C．2cm，3cm，5cm D．2cm，3cm，4cm
3．（3分）一个多边形的内角和是1800°，则这个多边形是（　　）边形．
A．9 B．10 C．11 D．12
4．（3分）下面四个图形分别是节能、节水、低碳和绿色食品标志，在这四个标志中，是轴对称图形的是（　　）
A． B． C． D．
5．（3分）一个多边形的内角和是外角和的2倍，这个多边形是（　　）
A．四边形 B．五边形 C．六边形 D．八边形
6．（3分）如图，三角形ABC，∠BAC＝90°，AD是三角形ABC的高，图中相等的是（　　）

A．∠B＝∠C B．∠BAD＝∠B C．∠C＝∠BAD D．∠DAC＝∠C
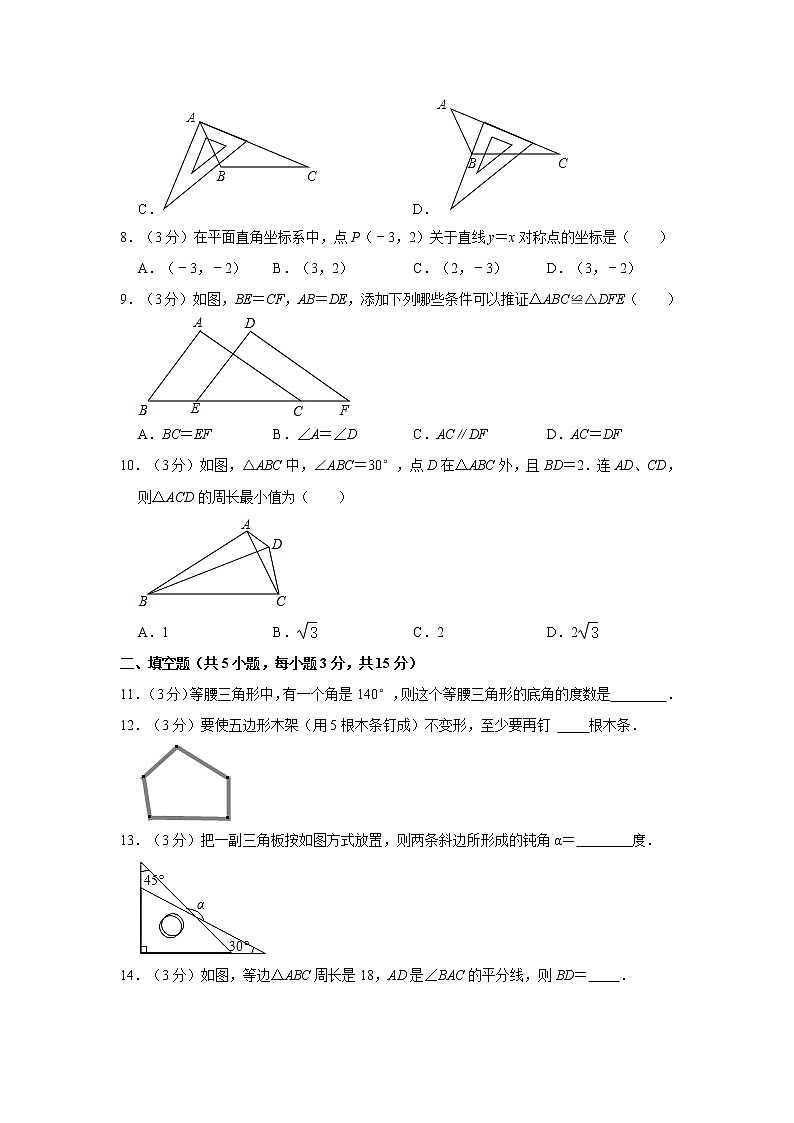
7．（3分）用三角板作△ABC的边BC上的高，下列三角板的摆放位置正确的是（　　）
A． B．
C． D．
8．（3分）在平面直角坐标系中，点P（﹣3，2）关于直线y＝x对称点的坐标是（　　）
A．（﹣3，﹣2） B．（3，2） C．（2，﹣3） D．（3，﹣2）
9．（3分）如图，BE＝CF，AB＝DE，添加下列哪些条件可以推证△ABC≌△DFE（　　）

A．BC＝EF B．∠A＝∠D C．AC∥DF D．AC＝DF
10．（3分）如图，△ABC中，∠ABC＝30°，点D在△ABC外，且BD＝2．连AD、CD，则△ACD的周长最小值为（　　）

A．1 B． C．2 D．2
二、填空题（共5小题，每小题3分，共15分）
11．（3分）等腰三角形中，有一个角是140°，则这个等腰三角形的底角的度数是　 　．
12．（3分）要使五边形木架（用5根木条钉成）不变形，至少要再钉 　 　根木条．

13．（3分）把一副三角板按如图方式放置，则两条斜边所形成的钝角α＝　 　度．

14．（3分）如图，等边△ABC周长是18，AD是∠BAC的平分线，则BD＝　 　．

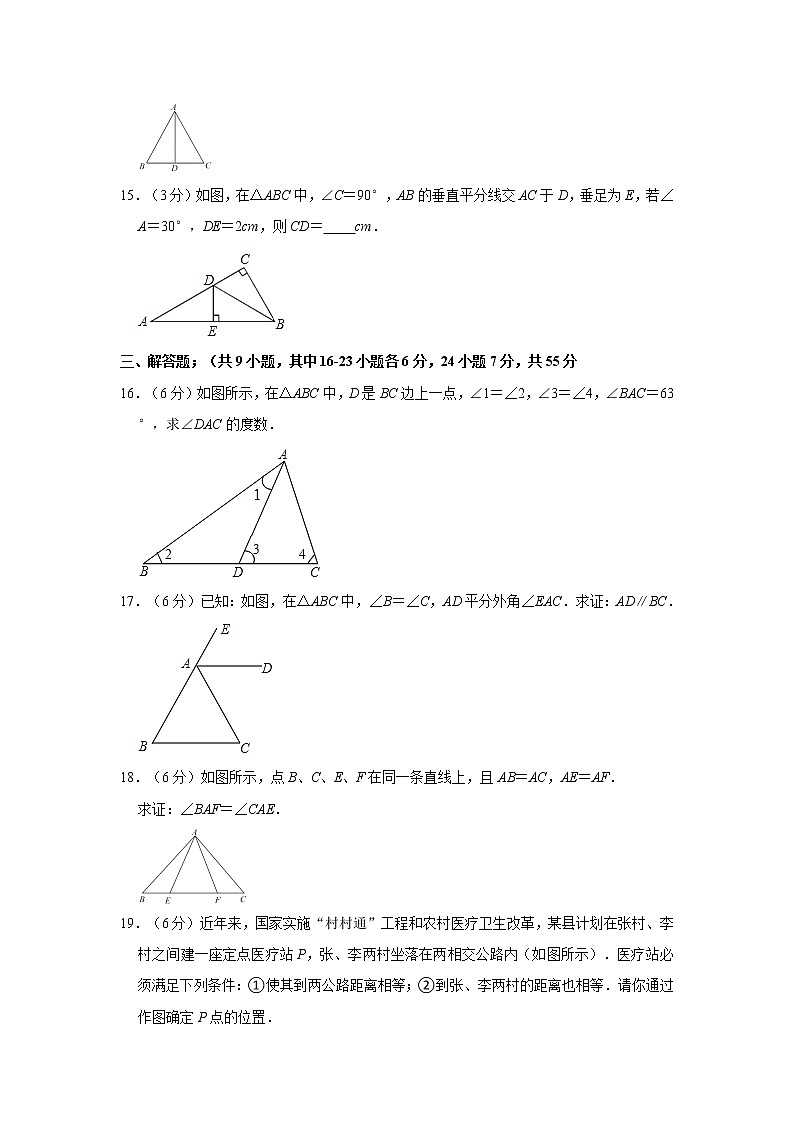
15．（3分）如图，在△ABC中，∠C＝90°，AB的垂直平分线交AC于D，垂足为E，若∠A＝30°，DE＝2cm，则CD＝　 　cm．

三、解答题；（共9小题，其中16-23小题各6分，24小题7分，共55分
16．（6分）如图所示，在△ABC中，D是BC边上一点，∠1＝∠2，∠3＝∠4，∠BAC＝63°，求∠DAC的度数．

17．（6分）已知：如图，在△ABC中，∠B＝∠C，AD平分外角∠EAC．求证：AD∥BC．

18．（6分）如图所示，点B、C、E、F在同一条直线上，且AB＝AC，AE＝AF．
求证：∠BAF＝∠CAE．

19．（6分）近年来，国家实施“村村通”工程和农村医疗卫生改革，某县计划在张村、李村之间建一座定点医疗站P，张、李两村坐落在两相交公路内（如图所示）．医疗站必须满足下列条件：①使其到两公路距离相等；②到张、李两村的距离也相等．请你通过作图确定P点的位置．

20．（6分）在平面直角坐标系xOy中，△ABC的位置如图所示．
（1）分别写出以下顶点的坐标：A（ 　 　，　 　）；B（ 　 　，　 　）．
（2）顶点A关于x轴对称的点A'的坐标（ 　 　，　 　），顶点C关于y轴对称的点C′的坐标（ 　 　，　 　）．
（3）求△ABC的面积．

21．（6分）如图，△ABC中，点O是∠ABC、∠ACB角平分线的交点，AB+BC+AC＝12，过O作OD⊥BC于D点，且OD＝2，求△ABC的面积．

22．（6分）如图，在△ABC中，AB＝AC，CD是∠ACB的平分线，DE∥BC，交AC于点E．
（1）求证：DE＝CE．
（2）若∠CDE＝35°，求∠A的度数．

23．（6分）如图，∠B＝∠C＝90°，E是BC的中点，DE平分∠ADC．
（1）求证：AE平分∠DAB；
（2）若AD＝8，BC＝6，求四边形ABCD的面积．

24．（7分）如图，△ABC是等边三角形．

（1）如图①，DE∥BC，分别交AB、AC于点D、E．求证：△ADE是等边三角形；
（2）如图②，△ADE仍是等边三角形，点B在ED的延长线上，连接CE，判断∠BEC的度数及线段AE、BE、CE之间的数量关系，并说明理由．

2021-2022学年山东省济宁市鱼台县八年级（上）期中数学试卷
参考答案与试题解析
一、选择题：（共10小题每小题3分共30分下面每小题只有一选项是正确的，请将正确选项涂在答题卡上
1．（3分）点M（﹣2，3）关于x轴对称点的坐标为（　　）
A．（﹣2，﹣3） B．（2，﹣3） C．（﹣3，﹣2） D．（2，3）
【分析】根据关于x轴对称的点，横坐标相同，纵坐标互为相反数，可得答案．
【解答】解：M（﹣2，3）关于x轴对称点的坐标为（﹣2，﹣3），
故选：A．
2．（3分）下面三根木条能组成三角形的是（　　）
A．1cm，2cm，5cm B．2cm，2cm，4cm
C．2cm，3cm，5cm D．2cm，3cm，4cm
【分析】根据三角形三边关系定理：三角形两边之和大于第三边，三角形的两边差小于第三边，可选出答案．
【解答】解：A、1+2＜5，故此选项不符合题意；
B、2+2＝4，故此选项不符合题意；
C、2+3＝5，故此选项不符合题意；
D、2+3＞4，故此选项符合题意．
故选：D．
3．（3分）一个多边形的内角和是1800°，则这个多边形是（　　）边形．
A．9 B．10 C．11 D．12
【分析】根据n边形的内角和是（n﹣2）180°，根据多边形的内角和为1800°，就得到一个关于n的方程，从而求出边数．
【解答】解：根据题意得：
（n﹣2）180＝1800，
解得：n＝12．
故选：D．
4．（3分）下面四个图形分别是节能、节水、低碳和绿色食品标志，在这四个标志中，是轴对称图形的是（　　）
A． B． C． D．
【分析】结合轴对称图形的概念进行求解即可．
【解答】解：A、不是轴对称图形，本选项不符合题意；
B、不是轴对称图形，本选项不符合题意；
C、不是轴对称图形，本选项不符合题意；
D、是轴对称图形，本选项符合题意．
故选：D．
5．（3分）一个多边形的内角和是外角和的2倍，这个多边形是（　　）
A．四边形 B．五边形 C．六边形 D．八边形
【分析】此题可以利用多边形的外角和和内角和定理求解．
【解答】解：设所求多边形边数为n，由题意得
（n﹣2）•180°＝360°×2
解得n＝6．
则这个多边形是六边形．
故选：C．
6．（3分）如图，三角形ABC，∠BAC＝90°，AD是三角形ABC的高，图中相等的是（　　）

A．∠B＝∠C B．∠BAD＝∠B C．∠C＝∠BAD D．∠DAC＝∠C
【分析】由三角形高的定义可得∠ADB＝∠ADC＝90°＝∠BAC，由三角形内角和定理和直角三角形的性质可求解．
【解答】解：∵AD是三角形ABC的高，
∴∠ADB＝∠ADC＝90°＝∠BAC，
∴∠B+∠C＝90°，∠BAD+∠B＝90°，∠C+∠CAD＝90°，
∴∠B＝∠DAC，∠C＝∠BAD，
故选：C．
7．（3分）用三角板作△ABC的边BC上的高，下列三角板的摆放位置正确的是（　　）
A． B．
C． D．
【分析】根据高线的定义即可得出结论．
【解答】解：B，C，D都不是△ABC的边BC上的高，
故选：A．
8．（3分）在平面直角坐标系中，点P（﹣3，2）关于直线y＝x对称点的坐标是（　　）
A．（﹣3，﹣2） B．（3，2） C．（2，﹣3） D．（3，﹣2）
【分析】作出图形，过点P作y轴的垂线与直线y＝x相交，再过交点作x轴的垂线，然后根据线段垂直平分线上的点到两端点的距离相等求解即可．
【解答】解：如图所示，点P（﹣3，2）关于直线y＝x对称点的坐标是（2，﹣3）．

故选：C．
9．（3分）如图，BE＝CF，AB＝DE，添加下列哪些条件可以推证△ABC≌△DFE（　　）

A．BC＝EF B．∠A＝∠D C．AC∥DF D．AC＝DF
【分析】要使△ABC≌△DEF，已知AB＝ED，BE＝CF，具备了两条边对应相等，还缺少边或角对应相等的条件，结合判定方法及图形进行选择即可．
【解答】解：可添加AC＝DF，或AB∥DE或∠B＝∠DEF，
证明添加AC＝DF后成立，
∵BE＝CF，
∴BC＝EF，
又AB＝DE，AC＝DF，
∴△ABC≌△DEF．
故选：D．
10．（3分）如图，△ABC中，∠ABC＝30°，点D在△ABC外，且BD＝2．连AD、CD，则△ACD的周长最小值为（　　）

A．1 B． C．2 D．2
【分析】作D关于直线BA的对称点M，直线BC的对称点N，连接MN，则线段MN的长度即为△ACD的周长的最小值，根据对称的性质得到∠MBA＝∠DBA，∠NBD＝∠DBC，BM＝BD＝BN，得到△MBN是等边三角形，于是得到结论．
【解答】解：作D关于直线BA的对称点M，直线BC的对称点N，连接MN，则线段MN的长度即为△ACD的周长的最小值，
由对称的性质得到∠MBA＝∠DBA，∠NBD＝∠DBC，BM＝BD＝BN，
∴∠MBA+∠NBC＝∠ABC＝30°，
∴∠MBN＝60°，
∴△MBN是等边三角形，
∴MN＝BM＝BD＝2，
∴△ACD的周长最小值为2，
故选：C．

二、填空题（共5小题，每小题3分，共15分）
11．（3分）等腰三角形中，有一个角是140°，则这个等腰三角形的底角的度数是　20°　．
【分析】根据数据，140°内角只能是顶角，利用三角形内角和定理求解即可．
【解答】解：根据题意，140°内角为顶角，
∴底角＝（180°﹣140°）＝20°．
故答案为：20°．
12．（3分）要使五边形木架（用5根木条钉成）不变形，至少要再钉 　2　根木条．

【分析】三角形具有稳定性，其它多边形不具有稳定性，把多边形分割成三角形则多边形的形状就不会改变．
【解答】解：再钉上两根木条，就可以使五边形分成三个三角形．故至少要再钉两根木条．
13．（3分）把一副三角板按如图方式放置，则两条斜边所形成的钝角α＝　165　度．

【分析】根据三角形的一个外角等于与它不相邻的两个内角的和或者根据四边形的内角和等于360°得出．
【解答】解：本题有多种解法．
解法一：∠α为下边小三角形外角，∠α＝30°+135°＝165°；
解法二：利用四边形内角和，∠α等于它的对顶角，故∠α＝360°﹣90°﹣60°﹣45°＝165°．
14．（3分）如图，等边△ABC周长是18，AD是∠BAC的平分线，则BD＝　3　．

【分析】由等边三角形的性质可求AB＝BC＝AC＝6，由等腰三角形的“三线合一”可求BD＝3．
【解答】解：∵等边△ABC周长是18，
∴AB＝BC＝AC＝6，
∵AD是∠BAC的平分线，AB＝BC＝AC＝6，
∴BD＝CD＝3，
故答案为：3．
15．（3分）如图，在△ABC中，∠C＝90°，AB的垂直平分线交AC于D，垂足为E，若∠A＝30°，DE＝2cm，则CD＝　2　cm．

【分析】根据线段垂直平分线的性质，可得∠ABD＝30°，结合已知，可得BD是∠ABC的角平分线，根据角平分线的性质，即可得出CD的长度；
【解答】解：∵DE是AB的垂直平分线，
∴AD＝BD，∠A＝30°，
∴∠DBA＝∠A＝30°，
∵∠C＝90°，
∴∠DBC＝30°，
即BD是∠ABC的角平分线，
∵DE⊥AB，DC⊥BC，
∴DE＝CD，DE＝2cm，
∴CD＝2cm；
故答案为：2．
三、解答题；（共9小题，其中16-23小题各6分，24小题7分，共55分
16．（6分）如图所示，在△ABC中，D是BC边上一点，∠1＝∠2，∠3＝∠4，∠BAC＝63°，求∠DAC的度数．

【分析】△ABD中，由三角形的外角性质知∠3＝2∠2，因此∠4＝2∠2，从而可在△BAC中，根据三角形内角和定理求出∠4的度数，进而可在△DAC中，由三角形内角和定理求出∠DAC的度数．
【解答】解：设∠1＝∠2＝x，则∠3＝∠4＝2x．
因为∠BAC＝63°，
所以∠2+∠4＝117°，即x+2x＝117°，
所以x＝39°；
所以∠3＝∠4＝78°，
∠DAC＝180°﹣∠3﹣∠4＝24°．
17．（6分）已知：如图，在△ABC中，∠B＝∠C，AD平分外角∠EAC．求证：AD∥BC．

【分析】根据三角形的一个外角等于与它不相邻的两个内角的和可得∠EAC＝∠B+∠C，再根据角平分线的定义可得∠EAC＝2∠EAD，从而得到∠B＝∠EAD，然后根据同位角相等两直线平行证明即可．
【解答】证明：由三角形的外角性质得，∠EAC＝∠B+∠C，
∵∠B＝∠C，
∴∠EAC＝2∠B，
∵AD平分外角∠EAC，
∴∠EAC＝2∠EAD，
∴∠B＝∠EAD，
∴AD∥BC．
18．（6分）如图所示，点B、C、E、F在同一条直线上，且AB＝AC，AE＝AF．
求证：∠BAF＝∠CAE．

【分析】根据全等三角形的性质得到∠B＝∠C，∠AEF＝∠AFE，根据全等三角形的判定和性质定理即可得到结论．
【解答】证明：∵AB＝AC，
∴∠B＝∠C，
∵AE＝AF，
∴∠AEF＝∠AFE，
在△ABF与△ACE中，

∴△ABF≌△ACE（AAS），
∴∠BAF＝∠CAE．
19．（6分）近年来，国家实施“村村通”工程和农村医疗卫生改革，某县计划在张村、李村之间建一座定点医疗站P，张、李两村坐落在两相交公路内（如图所示）．医疗站必须满足下列条件：①使其到两公路距离相等；②到张、李两村的距离也相等．请你通过作图确定P点的位置．

【分析】画出两条公路夹角的平分线和张、李两村之间线段的垂直平分线，交点即是所求．
【解答】解：（1）画出角平分线；
（2）作出垂直平分线．
交点P即满足条件．

20．（6分）在平面直角坐标系xOy中，△ABC的位置如图所示．
（1）分别写出以下顶点的坐标：A（ 　﹣4　，　3　）；B（ 　3　，　0　）．
（2）顶点A关于x轴对称的点A'的坐标（ 　4　，　3　），顶点C关于y轴对称的点C′的坐标（ 　2　，　5　）．
（3）求△ABC的面积．

【分析】（1）直接利用坐标系得出△ABC各个顶点的坐标即可；
（2）利用关于坐标轴对称点的性质解答即可；关于x轴的对称点的坐标特点：横坐标不变，纵坐标互为相反数；关于y轴的对称点的坐标特点：横坐标互为相反数，纵坐标不变；
（3）直接利用割补法即可得出△ABC的面积．
【解答】解：（1）由图可得，A（﹣4，3），B（3，0），C（﹣2，5），
故答案为：﹣4，3，3，0；
（2）顶点A关于y轴对称的点A'的坐标为（4，3），
顶点C关于y轴对称的点C′的坐标（2，5），
故答案为：4，3，2，5；
（3）△ABC的面积为：
（4+3）×5﹣﹣+
＝
＝10．

21．（6分）如图，△ABC中，点O是∠ABC、∠ACB角平分线的交点，AB+BC+AC＝12，过O作OD⊥BC于D点，且OD＝2，求△ABC的面积．

【分析】作OE⊥AB于E，OF⊥AC于F，连接OA，如图，根据角平分线的性质得OE＝OF＝OD＝2，然后根据三角形面积公式和S△ABC＝S△ABO+S△BCO+S△ACO进行计算即可．
【解答】解：作OE⊥AB于E，OF⊥AC于F，连接OA，如图，
∵点O是∠ABC、∠ACB角平分线的交点，
∴OE＝OD，OF＝OD，
即OE＝OF＝OD＝2，
∴S△ABC＝S△ABO+S△BCO+S△ACO＝AB•OE+BC•OD+AC•OF
＝×2×（AB+BC+AC）
＝×2×12
＝12．

22．（6分）如图，在△ABC中，AB＝AC，CD是∠ACB的平分线，DE∥BC，交AC于点E．
（1）求证：DE＝CE．
（2）若∠CDE＝35°，求∠A的度数．

【分析】（1）根据角平分线的性质可得出∠BCD＝∠ECD，由DE∥BC可得出∠EDC＝∠BCD，进而可得出∠EDC＝∠ECD，再利用等角对等边即可证出DE＝CE；
（2）由（1）可得出∠ECD＝∠EDC＝35°，进而可得出∠ACB＝2∠ECD＝70°，再根据等腰三角形的性质结合三角形内角和定理即可求出∠A的度数．
【解答】（1）证明：∵CD是∠ACB的平分线，
∴∠BCD＝∠ECD．
∵DE∥BC，
∴∠EDC＝∠BCD，
∴∠EDC＝∠ECD，
∴DE＝CE．
（2）解：∵∠ECD＝∠EDC＝35°，
∴∠ACB＝2∠ECD＝70°．
∵AB＝AC，
∴∠ABC＝∠ACB＝70°，
∴∠A＝180°﹣70°﹣70°＝40°．

23．（6分）如图，∠B＝∠C＝90°，E是BC的中点，DE平分∠ADC．
（1）求证：AE平分∠DAB；
（2）若AD＝8，BC＝6，求四边形ABCD的面积．

【分析】（1）过点E作EF⊥DA于点F，首先根据角的平分线上的点到角的两边的距离相等可得CE＝EF，根据等量代换可得BE＝EF，再根据角平分线的判定可得AE平分∠BAD；
（2）根据角平分线的性质可得CD＝DF，AB＝AF，可求CD+AB，再利用梯形的面积公式可得答案．
【解答】（1）证明：过点E作EF⊥DA于点F，
∵∠C＝90°，DE平分∠ADC，
∴CE＝EF，
∵E是BC的中点，
∴BE＝CE，
∴BE＝EF，
又∵∠B＝90°，EF⊥AD，
∴AE平分∠DAB．

（2）解：∵∠C＝90°，DE平分∠ADC，EF⊥DA，
∴CD＝DF，
∵∠B＝90°，AE是∠DAB的平分线，
∴AB＝AF，
∴CD+AB＝DF+AF＝AD＝8，
∴S梯形ABCD＝8×6÷2＝24．

24．（7分）如图，△ABC是等边三角形．

（1）如图①，DE∥BC，分别交AB、AC于点D、E．求证：△ADE是等边三角形；
（2）如图②，△ADE仍是等边三角形，点B在ED的延长线上，连接CE，判断∠BEC的度数及线段AE、BE、CE之间的数量关系，并说明理由．
【分析】（1）根据等边三角形的性质得到∠B＝∠C＝60°，根据平行线的性质和等边三角形的判定定理证明即可；
（2）证明△BAD≌△CAE，得到BD＝CE即可证明．
【解答】（1）证明：∵△ABC是等边三角形，
∴∠B＝∠C＝60°，
∵DE∥BC，
∴∠ADE＝∠B＝60°，∠AED＝∠C＝60°，
∴△ADE是等边三角形；
（2）解：AE+CE＝BE．
∵∠BAD+∠DAC＝60°，∠CAE+∠DAC＝60°，
∴∠BAD＝∠CAE，
在△BAD和△CAE中，
，
∴△BAD≌△CAE（SAS），
∴BD＝CE，∠AEC＝∠ADB＝120°，
∴BE＝BD+DE＝AE+CE，∠BEC＝∠AEC﹣∠AED＝60°．