湘教版八年级下册1.4 角平分线的性质一等奖ppt课件

导入新课

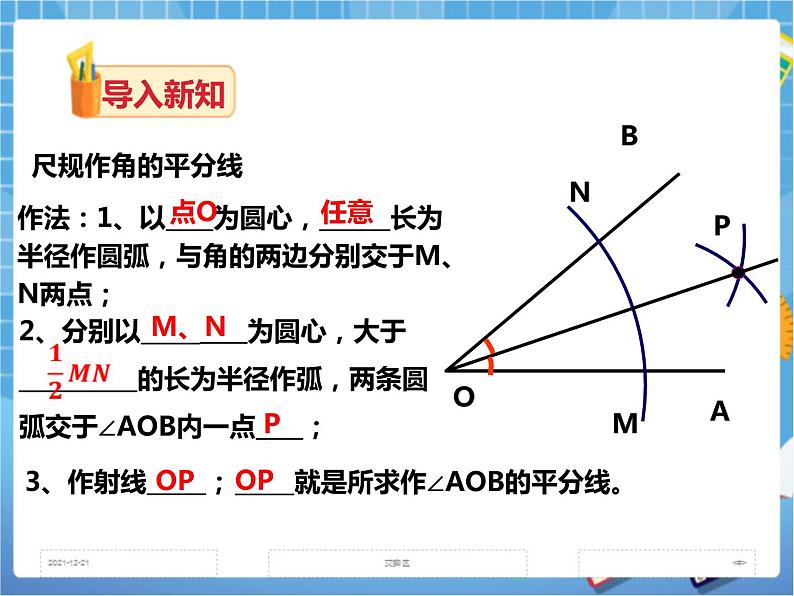
角平分线的概念

一条射线把一个角分成两个相等的角，这条射线叫做这个角的平分线。

尺规作角的平分线

作法：1、以____为圆心，______长为半径作圆弧，与角的两边分别交于M、N两点；

2、分别以_____为圆心，大于__________的长为半径作弧，两条圆弧交于∠AOB内一点____；

3、作射线_____；

_____就是所求作∠AOB的平分线。

学生解答问题

体验角平分线的作法，并为角平分线的性质定理的引出做铺垫，为下一步设置问题墙。

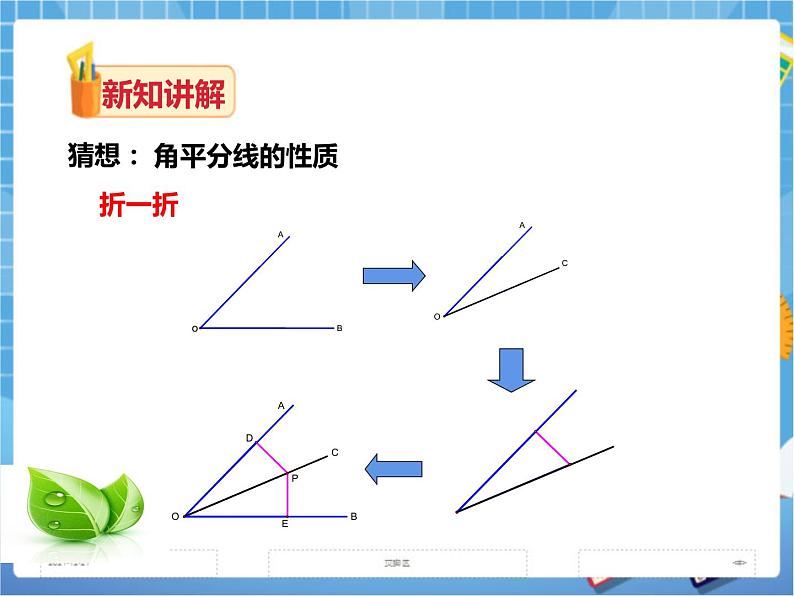
讲授新课

猜想：角平分线的性质

折一折

将AOB对折,在折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论?

角平分线上的点到角的两边的距离相等          

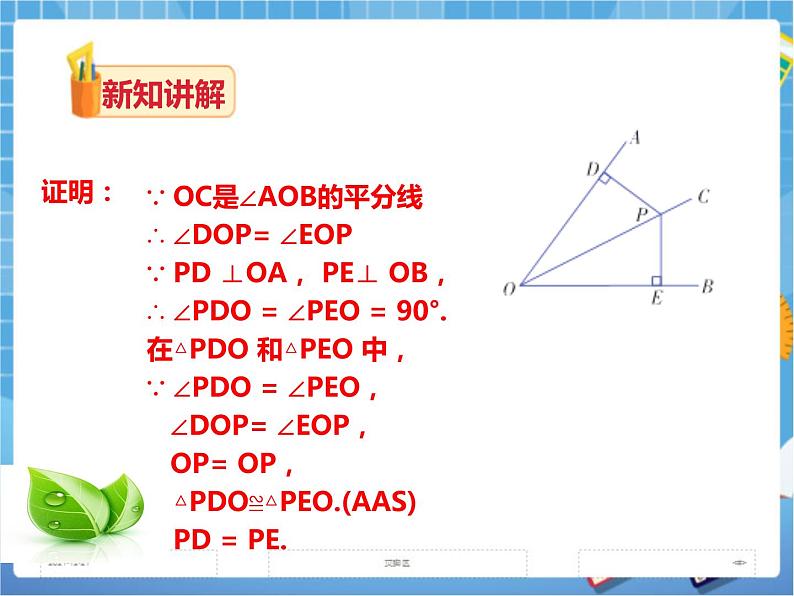
探究

如图，在∠AOB的平分线OC上任取一点P，作PD⊥OA，PE⊥OB，垂足分别为点D，E，试问PD与PE相等吗？

你能证明这个结论吗？

结论：

角平分线的性质定理

角的平分线上的点到角的两边的距离相等.

几何语言：

∵ OC是∠AOB的平分线

PD ⊥OA， PE⊥ OB

∴ PD = PE

定理应用所具备的条件：

(1)角的平分线；

(2)点在该平分线上

(3)垂直距离

定理的作用：证明线段相等

练习

如图，E 是∠AOB 的平分线上一点，EC⊥OA 于点C，ED⊥OB 于点D.

求证：（1）∠ECD=∠EDC； （2）OC=OD.

思考：角的内部到角的两边距离相等的点在这个角的平分线上吗？

如图，点P在∠AOB的内部，作PD⊥OA，PE⊥OB，垂足分别在点D，E.若PD=PE.

求证：点P在∠AOB的平分线上

结论：

角平分线的性质逆定理

角的内部到角的两边距离相等的点在角的平分线上.

几何语言：

∵ PD⊥OA， PE⊥OB

   PD = PE

∴OC是∠AOB的平分线

练习

已知，如图，AB=AC，BD=CD，DE⊥AB于点E，DF⊥AC于点F，求证：DE=DF

例1 如图，∠BAD=∠BCD=90 °， ∠1=∠2.

（1）求证：点B在∠ABC的平分线上。

（2）求证：BD是∠ABC的角平分线。

如图，在△ABC 中，AD⊥DE，BE⊥DE，AC，BC 分别平分∠BAD，∠ABE，点C在线段DE上.

求证：AB=AD+BE.

让学生在小组内共同合作，协手完成此活动．教师参与此活动，并给学生以提示、启发

学生实验

学生分组讨论,教师引导得出结论

学生分析已知条件,利用(AAS)证明.

学生自主解答，教师适时的进行提示

由学生自己独立完成，教师巡视学生的结果

学生自主解答，教师适时的进行提示

学生自主解答例题

让学生试着寻找解题思路；教师可引导学生发现证明的思路

通过折纸及作图过程，由学生自己去发现结论．教师要有足够的耐心，要为学生的思考留有时间和空间．

从实验探索中发现角的平分线的性质。

培养学生的数学抽象概括能力及理性精神.

让学生体验成功

通过此题的解答，充分调动学生动脑的积极性，培养学生发散思维。

增强学生解决问题以及总结归纳的能力。

通过此题的解答，使学生对知识的掌握进一步的提高

进一步理解和掌握角平分线性质定理与逆定理，提高学生的数学应用意识和逻辑推理能力．

通过学生对角的平分线的知识进行独立练习，自我评价学习效果，及时发现问题、解决知识盲点，培养学生的创新精神和实践能力。

巩固提升

1 .如图，∠1＝∠2，PD⊥OA，PE⊥OB，垂足分别为 D，E，下列结论错误的是（　　）

A、PD＝PE　       B、OD＝OE　

C、∠DPO＝∠EPO　 D、PD＝OD

答案：D

2.在△ABC中，∠C=90゜，AD平分∠BAC交BC于D，BD：DC=3：2，点D到AB的距离为6，则BC长为（　　）

A．10 B．20 C．15 D．25

答案：C

3、如图 ，OP平分∠MON，PA⊥ON于点A，点Q是射线OM上一个动点，若PA=3，则PQ的最小值为　   　．

答案：3

4、如图，AD∥BC，∠ABC的角平分 线BP与∠BAD的角平分线AP相交于点P，作PE⊥AB 于点E．若PE=2，则两平行线AD与BC间的距离为　   　．

答案：4

5、如图，在△ABC中，∠C=90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB于点E．

求证：AC=AE

答案：

证明：∵在△ABC中，∠C=90°，

AD平分∠CAB，DE⊥AB，

∴CD=DE，∠AED=∠C=90°，∠CAD=∠EAD，

在△ACD和△ AED中

∴△ACD≌△AED，

∴AC=AE

6.要在S区建一个集贸市场，使它到公路，铁路距离相等且离公路，铁路的交叉处500米，应建在何处？(比例1:20000)

答案：

解：设距离交点Oxm，
则：=，
解得：x=0.025，
0.025m=2.5cm．
OP=2.5cm．
点P即为所求．

学生自主解答，教师讲解答案。

鼓励学生认真思考；发现解决问题的方法，引导学生主动地参与教学活动，发扬数学民主，让学生在独立思考、合作交流等数学活动中，培养学生合作互助意识，提高数学交流与数学表达能力。

课堂小结

谈一谈本节的主要内容，畅所欲言聊收获。

学生归纳本节所学知识

培养学生总结，归纳的能力。

板书