专题02 ： 27.1 图形的相似 - 期末复习专题训练 2021-2022学年人教版数学九年级下册

这是一份专题02 ： 27.1 图形的相似 - 期末复习专题训练 2021-2022学年人教版数学九年级下册，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
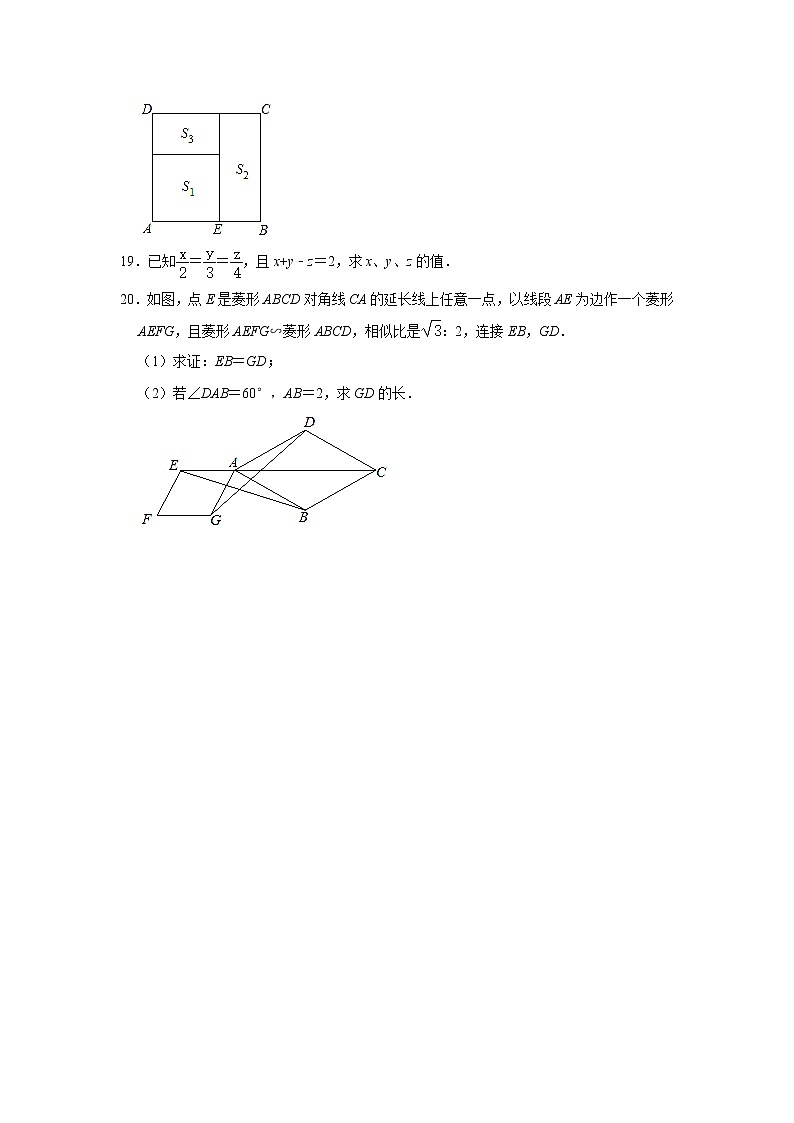
专题02 ：2022年人教新版九年级（下册）27.1 图形的相似 - 期末复习专题训练一、选择题（共10小题）1．若＝，则的值为（　　）A．5 B． C．3 D．2．两个相似多边形的面积之比是1：4，则这两个相似多边形的周长之比是（　　）A．1：2 B．1：4 C．1：8 D．1：163．如果C是线段AB的黄金分割点，并且AC＞CB，AB＝1，那么AC的长度为（　　）A． B． C． D．4．下面四组线段中，成比例的是（　　）A．a＝2，b＝3，c＝4，d＝5 B．a＝1，b＝2，c＝2，d＝4 C．a＝4，b＝6，c＝5  d＝10 D．a＝，b＝，c＝3，d＝5．若，则的值为（　　）A． B．﹣1 C．1 D．6．下列各组数中，不能组成比例的是（　　）A．2、4、4和8 B．0.3、6、0.2和4 C．2、5、7和15 D．、、和7．已知a：b＝2：3，那么下列等式中成立的是（　　）A．3a＝2b B．2a＝3b C． D．8．若2x﹣7y＝0，则x：y等于（　　）A．2：7 B．4：7 C．7：2 D．7：49．将直角三角形的三条边的长度都扩大同样的倍数后得到的三角形（　　）A．仍是直角三角形 B．一定是锐角三角形 C．可能是钝角三角形 D．一定是钝角三角形10．下列各组线段中，成比例的是（　　）A．2cm，3cm，4cm，5cm B．2cm，4cm，6cm，8cm C．3cm，6cm，8cm，12cm D．1cm，3cm，5cm，15cm二、填空题（共5小题）11．在2和8这两个数之间添上一个数，使之成为2与8的比例中项．这个数是　   　．12．若两个相似多边形的相似比是2：3，则它们的周长比是　    　．13．定义：如果三角形的两个内角∠α与∠β满足∠α＝2∠β，那么，我们将这样的三角形称为“倍角三角形”．如果一个等腰三角形是“倍角三角形”，那么这个等腰三角形的腰长与底边长的比值为　                　．14．定义：我们知道，四边形的一条对角线把这个四边形分成两个三角形，如果这两个三角形相似但不全等，我们就把这条对角线叫做这个四边形的相似对角线．在四边形ABCD中，对角线BD是它的相似对角线，∠ABC＝70°，BD平分∠ABC，那么∠ADC＝　    　度．15．已知≠0，则＝　 　．三、解答题（共5小题）16．如图所示，有矩形ABCD和矩形A′B′C′D′，AB＝8cm，BC＝12cm，A′B′＝4cm，B′C′＝6cm．（1）求和；（2）线段A′B′，AB，B′C′，BC是成比例线段吗？17．如图，点B是线段AC的黄金分割点，且AB＞BC，若AC＝2，求AB、BC的长．18．如图，点E是正方形ABCD的边AB边上的黄金分割点，且AE＞EB，S1表示AE为边长的正方形面积，S2表示以BC为长，BE为宽的矩形面积，S3表示正方形ABCD除去S1和S2剩余的面积，求S3：S2的值．19．已知＝＝，且x+y﹣z＝2，求x、y、z的值．20．如图，点E是菱形ABCD对角线CA的延长线上任意一点，以线段AE为边作一个菱形AEFG，且菱形AEFG∽菱形ABCD，相似比是：2，连接EB，GD．（1）求证：EB＝GD；（2）若∠DAB＝60°，AB＝2，求GD的长．
专题02 ：2022年人教新版九年级（下册）27.1 图形的相似 - 期末复习专题训练参考答案与试题解析一、选择题（共10小题）1．若＝，则的值为（　　）A．5 B． C．3 D．【解答】解：由＝，得4b＝a﹣b．，解得a＝5b，＝＝5，故选：A．2．两个相似多边形的面积之比是1：4，则这两个相似多边形的周长之比是（　　）A．1：2 B．1：4 C．1：8 D．1：16【解答】解：∵两个相似多边形的面积之比是1：4，∴这两个相似多边形的相似比是1：2，则这两个相似多边形的周长之比是1：2，故选：A．3．如果C是线段AB的黄金分割点，并且AC＞CB，AB＝1，那么AC的长度为（　　）A． B． C． D．【解答】解：∵C是线段AB的黄金分割点，AC＞CB，∴AC＝AB＝，故选：C．4．下面四组线段中，成比例的是（　　）A．a＝2，b＝3，c＝4，d＝5 B．a＝1，b＝2，c＝2，d＝4 C．a＝4，b＝6，c＝5  d＝10 D．a＝，b＝，c＝3，d＝【解答】解：A、2×5≠3×4，故选项错误；B、1×4＝2×2，故选项正确；C、4×10≠5×6，故选项错误；D、×3≠×，故选项错误．故选：B．5．若，则的值为（　　）A． B．﹣1 C．1 D．【解答】解：由，得2x＝x﹣y，∴x＝﹣y，∴＝﹣1，故选：B．6．下列各组数中，不能组成比例的是（　　）A．2、4、4和8 B．0.3、6、0.2和4 C．2、5、7和15 D．、、和【解答】解：A、2×8＝4×4，能组成比例，故本选项不符合题意；B、4×0.3＝6×0.2，能组成比例，故本选项不符合题意；C、2×15≠5×7，不能组成比例，故本选项符合题意；D、×＝×，能组成比例，故本选项不符合题意．故选：C．7．已知a：b＝2：3，那么下列等式中成立的是（　　）A．3a＝2b B．2a＝3b C． D．【解答】解：∵a：b＝2：3的两内项是b、2，两外项是a、3，∴3a＝2b；A、3a＝2b；故本选项正确；B、2a＝3b；故本选项错误；C、由得，2a+2b＝5b，即2a＝3b；故本选项错误；D、由得，3a﹣3b＝b，即3a＝4b；故本选项错误；故选：A．8．若2x﹣7y＝0，则x：y等于（　　）A．2：7 B．4：7 C．7：2 D．7：4【解答】解：∵2x﹣7y＝0，∴2x＝7y，∴x：y＝7：2．故选：C．9．将直角三角形的三条边的长度都扩大同样的倍数后得到的三角形（　　）A．仍是直角三角形 B．一定是锐角三角形 C．可能是钝角三角形 D．一定是钝角三角形【解答】解：∵将直角三角形的各边都缩小或扩大同样的倍数后，得到的三角形的三条边与原三角形的三条边对应成比例，∴两三角形相似．又∵原来的三角形是直角三角形，而相似三角形的对应角相等，∴得到的三角形仍是直角三角形．故选：A．10．下列各组线段中，成比例的是（　　）A．2cm，3cm，4cm，5cm B．2cm，4cm，6cm，8cm C．3cm，6cm，8cm，12cm D．1cm，3cm，5cm，15cm【解答】解：A、∵2×5≠3×4，∴选项A不成比例；B、∵2×8≠4×6，∴选项B不成比例；C、∵3×12≠6×8，∴选项C不成比例；D、∵1×15＝3×5，∴选项D成比例．故选：D．二、填空题（共5小题）11．在2和8这两个数之间添上一个数，使之成为2与8的比例中项．这个数是　±4　．【解答】解：设2和8的比例中项是x，则：x2＝2×8，解得x＝±4，故答案为：±4．12．若两个相似多边形的相似比是2：3，则它们的周长比是　2：3　．【解答】解：∵两个相似多边形的相似比是2：3，∴它们的周长比是：2：3．故答案为：2：3．13．定义：如果三角形的两个内角∠α与∠β满足∠α＝2∠β，那么，我们将这样的三角形称为“倍角三角形”．如果一个等腰三角形是“倍角三角形”，那么这个等腰三角形的腰长与底边长的比值为　或　．【解答】解：若等腰三角形的三个内角∠α、∠β，∠β，∵∠α+2∠β＝180°，∠α＝2∠β，∴4∠β＝180°，解得β＝45°，∴此“倍角三角形”为等腰直角三角形，∴腰长与底边长的比值为；若等腰三角形的三个内角∠α、∠α，∠β，∵2∠α+∠β＝180°，∠α＝2∠β，∴5∠β＝180°，解得β＝36°，如图，∠B＝∠C＝72°，∠A＝36°，作∠ABC的平分线BD，则∠ABD＝∠CBD＝36°，∴DA＝DB，∵∠BDC＝∠A+∠ABD＝72°，∴∠BDC＝∠C，∴BD＝BC，即DA＝DB＝CB，∵∠CBD＝∠A，∠BCD＝∠ACB，∴△BDC∽△ACB，∴BC：AC＝CD：BC，即BC：AC＝（AC﹣BC）：BC，整理得AC2﹣AC•BC﹣BC2＝0，解得AC＝BC，即＝，此时腰长与底边长的比值为，综上所述，这个等腰三角形的腰长与底边长的比值为或．故答案为或．14．定义：我们知道，四边形的一条对角线把这个四边形分成两个三角形，如果这两个三角形相似但不全等，我们就把这条对角线叫做这个四边形的相似对角线．在四边形ABCD中，对角线BD是它的相似对角线，∠ABC＝70°，BD平分∠ABC，那么∠ADC＝　145　度．【解答】解：如图所示，∵∠ABC＝70°，BD平分∠ABC，∴∠ABD＝∠DBC，又∵对角线BD是它的相似对角线，∴△ABD∽△DBC，∴∠A＝∠BDC，∠ADB＝∠C，∴∠A+∠C＝∠ADC，又∵∠A+∠C+∠ADC＝360°﹣70°＝290°，∴∠ADC＝145°，故答案为：145．15．已知≠0，则＝　3　．【解答】解：设＝k，则a＝3k，b＝4k，c＝5k，＝＝3．故答案为：3．三、解答题（共5小题）16．如图所示，有矩形ABCD和矩形A′B′C′D′，AB＝8cm，BC＝12cm，A′B′＝4cm，B′C′＝6cm．（1）求和；（2）线段A′B′，AB，B′C′，BC是成比例线段吗？【解答】解：（1）∵AB＝8cm，BC＝12cm，A′B′＝4cm，B′C′＝6cm．∴＝＝，＝＝； （2）由（1）知＝＝，＝＝；∴＝，∴线段A′B′，AB，B′C′，BC是成比例线段．17．如图，点B是线段AC的黄金分割点，且AB＞BC，若AC＝2，求AB、BC的长．【解答】解：∵点B是线段AC的黄金分割点，且AB＞BC，∴AB＝×AC＝﹣1，∴BC＝AC﹣AB＝2﹣（﹣1）＝3﹣．18．如图，点E是正方形ABCD的边AB边上的黄金分割点，且AE＞EB，S1表示AE为边长的正方形面积，S2表示以BC为长，BE为宽的矩形面积，S3表示正方形ABCD除去S1和S2剩余的面积，求S3：S2的值．【解答】解：如图，设AB＝1，∵点E是正方形ABCD的边AB边上的黄金分割点，且AE＞EB，∴AE＝GF＝，∴BE＝FH＝AB﹣AE＝，∴S3：S2＝（GF•FH）：（BC•BE）＝（×）：（1×）＝．故答案为：．19．已知＝＝，且x+y﹣z＝2，求x、y、z的值．【解答】解：设＝＝＝k，得x＝2k，y＝3k，z＝4k．将x＝2k，y＝3k，z＝4k代入x+y﹣z＝2，得2k+3k﹣4k＝2．解得k＝2．x＝2k＝4，y＝3k＝6，z＝4k＝8．20．如图，点E是菱形ABCD对角线CA的延长线上任意一点，以线段AE为边作一个菱形AEFG，且菱形AEFG∽菱形ABCD，相似比是：2，连接EB，GD．（1）求证：EB＝GD；（2）若∠DAB＝60°，AB＝2，求GD的长．【解答】（1）证明：∵菱形AEFG∽菱形ABCD，∴∠EAG＝∠BAD，∴∠EAG+∠GAB＝∠BAD+∠GAB，∴∠EAB＝∠GAD，∵AE＝AG，AB＝AD，∴△AEB≌△AGD，∴EB＝GD；（2）连接BD交AC于点P，则BP⊥AC，∵∠DAB＝60°，∴∠PAB＝30°，∵菱形AEFG∽菱形ABCD，相似比是：2，AB＝2，∴AE＝，BP＝AB＝1，∴AP＝，∴EP＝，∴EB＝，∴GD＝．