2021-2022学年鲁教版（五四制）七年级数学第一学期期末综合复习模拟测试题1（word版 含答案）

2021-2022学年鲁教版七年级数学第一学期期末综合复习模拟测试题1（附答案）

一、选择题（共12小题，满分36分.）

1．在实数：，π，，，2π，，0.36，0.3737737773…（相邻两个3之间7的个数逐次加1），﹣，，无理数的个数为（　　）

A．4 B．5 C．6 D．7

2．如图，在方格纸上，用（1，1）表示点A的位置，用（2，3）表示点C的位置，则点B的位置表示为（　　）

A．（3，1） B．（3，2） C．（4，2） D．（4，3）

3．根据你对函数概念的理解，下列曲线表示的函数中，y不是x的函数的是（　　）

A．B．C．D．

4．下列各组数，互为相反数的是（　　）

A．﹣2与 B．|﹣|与 C．﹣2与（﹣）2 D．2与

5．一次函数y＝﹣2x+6与x轴的交点坐标是（　　）

A．（3，0） B．（﹣3，0） C．（0，3） D．（0，﹣3）

6．已知点（1，m）和点（3，n）是一次函数y＝﹣2x+h图象上的两个点，则m与n的大小关系是（　　）

A．m＞n B．m＜n C．m＝n D．以上都不对

7．如图，已知点P（a，b）在第二象限，则一次函数y＝﹣ax+2b的图象可能是（　　）

A．B．C．D．

8．如图，点A、B、C分别是同一数轴上的三个点，且AB＝AC，A、B两点对应的实数分别是1和﹣，则点C位于下列哪两个相邻整数之间（　　）

A．3和4 B．2和3 C．1和2 D．4和5

9．某油箱容量为60 L的汽车，加满汽油后行驶了100 km时，油箱中的汽油大约消耗了，如果加满汽油后汽车行驶的路程为xkm，油箱中剩油量为yL，则y与x之间的函数解析式和自变量取值范围分别是（　　）

A．y＝0.12x，x＞0 B．y＝60﹣0.12x，x＞0 

C．y＝0.12x，0≤x≤500 D．y＝60﹣0.12x，0≤x≤500

10．已知点P（3，a）关于x轴的对称点为Q（b，2），则ab＝（　　）

A．6 B．﹣6 C．5 D．﹣5

11．如图，Rt△ABC中，AB＝9，BC＝6，∠B＝90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，则线段BN的长为（　　）

A． B． C．4 D．5

12．A，B两地相距20千米，甲、乙两人都从A地去B地，图中l1和l2分别表示甲、乙两人所走路程s（千米）与时间t（小时）之间的关系．对于下列说法：

①乙晚出发1小时：②乙出发3小时后追上甲；

③甲的速度是6千米/小时；④乙先到达B地．其中正确的个数是（　　）

A．4个 B．3个 C．2个 D．1个

二、填空题（共6小题，满分24分.）

13．在平面直角坐标系中，已知一次函数y＝2x+1的图象经过P1（﹣1，y1），P2（2，y2）两点，则y1　   　y2（填“＞”或“＜”或“＝”）．

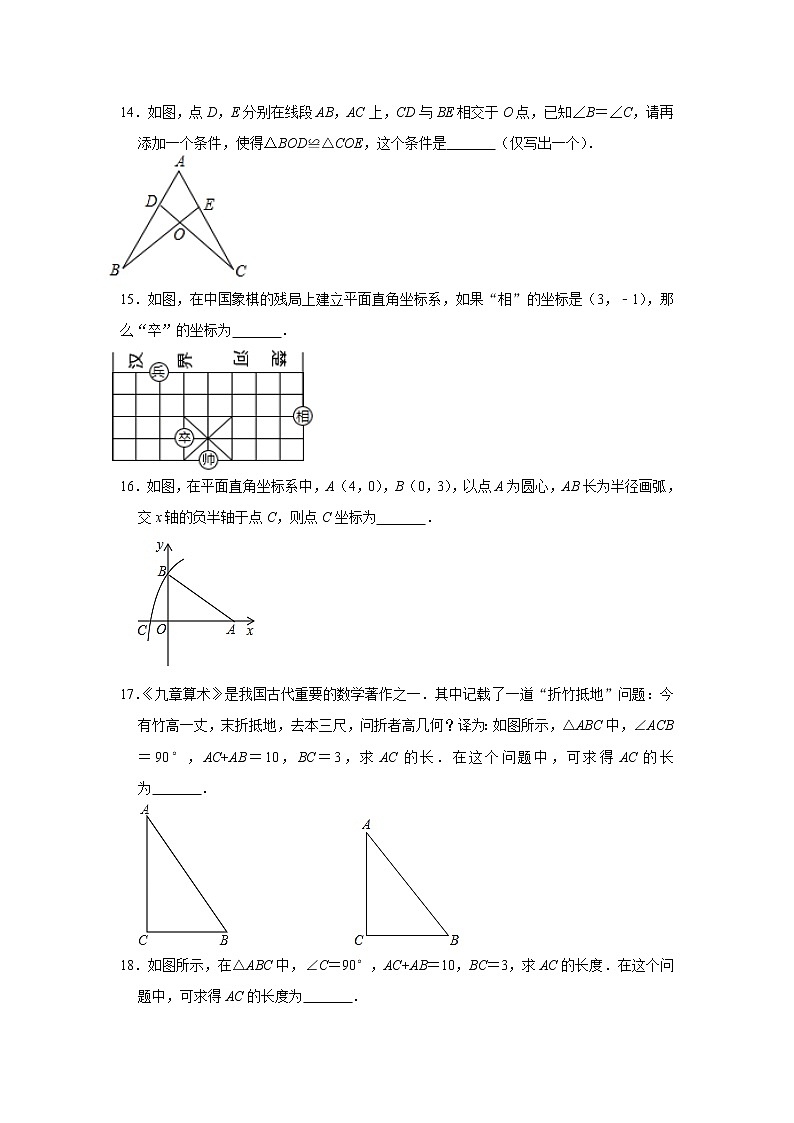
14．如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，已知∠B＝∠C，请再添加一个条件，使得△BOD≌△COE，这个条件是　   　（仅写出一个）．

15．如图，在中国象棋的残局上建立平面直角坐标系，如果“相”的坐标是（3，﹣1），那么“卒”的坐标为　   　．

16．如图，在平面直角坐标系中，A（4，0），B（0，3），以点A为圆心，AB长为半径画弧，交x轴的负半轴于点C，则点C坐标为　   　．

17．《九章算术》是我国古代重要的数学著作之一．其中记载了一道“折竹抵地”问题：今有竹高一丈，末折抵地，去本三尺，问折者高几何？译为：如图所示，△ABC中，∠ACB＝90°，AC+AB＝10，BC＝3，求AC的长．在这个问题中，可求得AC的长为　   　．

18．如图所示，在△ABC中，∠C＝90°，AC+AB＝10，BC＝3，求AC的长度．在这个问题中，可求得AC的长度为　   　．

三.解答下列各题：（共7小题，满分60分.）

19．计算：﹣+（﹣）﹣2+（π﹣3.14）0﹣（）2

20．如图，在△ABC中，AD是BC边上的高，AE平分∠BAC，∠C＝46°，∠DAE＝10°，求∠B的度数．

21．如图，在平面直角坐标系中，每个小正方形的边长为1，点A的坐标为（﹣3，2）．请按要求分别完成下列各小题：

（1）画出△ABC关于y轴对称的△A1B1C1，则点C1的坐标是　   　；

（2）△ABC的面积是多少？

22．如图，四边形ABCD中，∠C＝90°，BD平分∠ABC，AD＝3，E为AB上一点，AE＝4，ED＝5，求CD的长．

23．如图，点A的坐标为（﹣，0），点B的坐标为（0，3）．

（1）求过A，B两点直线的函数表达式；

（2）过B点作直线BP与x轴交于点P，且使OP＝2OA，求△ABP的面积．

24如图1，在直角梯形ABCD中，动点P从B点出发，沿B→C→D→A匀速运动，设点P运动的路程为x，△ABP的面积为y，图象如图2所示．

（1）当点P运动的路程x＝4时，△ABP的面积为y＝　   　；

（2）求：线段AB的长；

（3）求：梯形ABCD的面积是多少？

25．[材料阅读]

材料一：如图1，∠AOB＝90°，点P在∠AOB的平分线OM上，∠CPD＝90°，点C，分别在OA，OB上．可求得如下结论：PC﹣PD； OC+OD为定值．

材料二：（性质）：四边形的内角和为360°．

[问题解决]

（1）如图2，点P在∠AOB的平分线OM上，PE⊥OA，OP＝m，PE＝n，∠CPD的边OA，OB交于点C，D，且∠AOB+∠CPD＝180°，求OC+OD的值（用含m．n的式子表示）．

（2）如图2，在平面直角坐标系中，直线y＝﹣x+7与y轴，x轴分别交于A，B两点，点P是AB的中点，∠CPD＝90°，PC与y轴交于点C，PD与x轴的正半轴交于点D，OC＝2，连接CD．求CD的长度．

参考答案:

一、选择题（共12小题，满分36分.）

1．解：因为＝3，＝2，＝，

所以无理数有：π，，2π，0.3737737773…（相邻两个3之间7的个数逐次加1）共4个．

故选：A．

2．解：如图，点B的位置为（4，2）．

故选C．

3．解：根据函数的意义可知：对于自变量x的任何值，y都有唯一的值与之相对应，所以B不正确．

故选：B．

4．解：﹣2与（﹣）2互为相反数，

故选：C．

5．解：当y＝0时，0＝﹣2x+6，

∴x＝3，

即直线y＝﹣2x+6与x轴的交点坐标为（3，0），

故选：A．

6．解：∵点（1，m）和点（3，n）是一次函数y＝﹣2x+h图象上的两个点，

∴m＝﹣2+h，n＝﹣6+h．

∵﹣2+h＞﹣6+h，

∴m＞n．

故选：A．

7．解：∵点P（a，b）在第二象限，

∴a＜0，b＞0，

∴﹣a＞0，2b＞0，

∴y＝﹣ax+2b经过一、二、三象限．

故选：B．

8．解：设点C所表示的数为x，

∵点B与点C到点A的距离相等，

∴AC＝AB，即x﹣1＝1+，

解得：x＝2+．

∵，

∴，

即点C位于3和4之间．

故选：A．

9．解：因为油箱容量为60 L的汽车，加满汽油后行驶了100 km时，油箱中的汽油大约消耗了，

可得：L/km，60÷0.12＝500（km），

所以y与x之间的函数解析式和自变量取值范围是：y＝60﹣0.12x，（0≤x≤500），

故选：D．

10．解：∵点P（3，a）关于x轴的对称点为Q（b，2），

∴a＝﹣2，b＝3，

∴ab＝﹣6，

故选：B．

11．解：设BN＝x，由折叠的性质可得DN＝AN＝9﹣x，

∵D是BC的中点，

∴BD＝3，

在Rt△BDN中，x2+32＝（9﹣x）2，

解得x＝4．

故线段BN的长为4．

故选：C．

12．解：由图可知，

乙晚出发1小时，故①正确；

乙出发3﹣1＝2小时后追上甲，故②错误；

甲的速度是：18÷3＝6（千米/小时），故③正确；

乙先到达B地，故④正确；

故选：B．

二、填空题（共6小题，满分24分.）

13．解：∵一次函数y＝2x+1中k＝2＞0，

∴y随x的增大而增大，

∵﹣1＜2，

∴y1＜y2．

故答案为：＜．

14．解：∵∠B＝∠C，∠BOD＝∠COE，

∵OB＝OC，

∴△BOD≌△COE（ASA）

∵OD＝OE，

∴△BOD≌△COE（AAS），

∵BD＝CE，

∴△BOD≌△COE（AAS），

故答案为：OB＝OC．

15．解：如图所示，

“卒”的坐标为（﹣2，﹣2），

故答案为：（﹣2，﹣2）．

16解：∵点A，B的坐标分别为（4，0），（0，3），

∴OA＝4，OB＝3，

在Rt△AOB中，由勾股定理得：AB＝＝5，

∴AC＝AB＝5，

∴OC＝5﹣4＝1，

∴点C的坐标为（﹣1，0），

故答案为：（﹣1，0），

17．解：设AC＝x，

∵AC+AB＝10，

∴AB＝10﹣x．

在Rt△ABC中，∠ACB＝90°，

∴AC2+BC2＝AB2，即x2+32＝（10﹣x）2．

解得：x＝4.55，

即AC＝4.55．

故答案为：4.55．

18．解：∵AC+AB＝10，

∴AB＝10﹣AC，

由勾股定理得，AC2+BC2＝AB2，即AC2+32＝（10﹣AC）2，

解得，AC＝，

故答案为：．

三.解答下列各题：（共7小题，满分60分.）

19．解：﹣+（﹣）﹣2+（π﹣3.14）0﹣（）2

＝8﹣++1﹣

＝9

20．解：∵AD⊥BC，

∴∠ADC＝90°，

∵∠C＝46°

∴∠CAD＝44°，

∵∠DAE＝10°，

∴∠CAE＝34°，

∵AE平分∠BAC，

∴∠BAC＝2∠EAC＝68°，

∴∠B＝180°﹣68°﹣46°＝66°．

21．解：（1）如图，△A1B1C1为所作；则点C1的坐标是（5，3）；

故答案为（5，3）；

（2）△ABC的面积＝2×3﹣×1×2﹣×3×1﹣×1×2＝2.5．

22．解：∵AD＝3，AE＝4，ED＝5，

∴AD2+AE2＝ED2．

∴∠A＝90°．

∴DA⊥AB．

∵∠C＝90°．

∴DC⊥BC．

∵BD平分∠ABC，

∴DC＝AD．

∵AD＝3，

∴CD＝3．

23．解：（1）设过A，B两点的直线解析式为y＝ax+b（a≠0），则根据题意，得，

解得，，

则过A，B两点的直线解析式为y＝2x+3；

（2）设P点坐标为（x，0），依题意得x＝±3，所以P点坐标分别为P1（3，0），P2（﹣3，0）．

＝＝，

＝×（3﹣）×3＝，

所以，△ABP的面积为或．

24．解：（1）由图象得：x＝4时，△ABP的面积为y＝16；

故答案为：16；

（2）根据图象得：BC＝4，此时△ABP为16，

∴AB•BC＝16，即×AB×4＝16，

解得：AB＝8；

（3）由图象得：DC＝9﹣4＝5，

则S梯形ABCD＝×BC×（DC+AB）＝×4×（5+8）＝26．

25．解：（1）如图1，作PF⊥OB，PE⊥OC，

P在∠AOB的平分线OM上，则PE＝PF，

则△PFD≌△PEC（AAS），

∴EC＝ED，而OE＝OF

所以CO+OD＝2OE，

在Rt△OPE中，OE＝＝

所以OC+OD＝2；

（2）当点C在y轴上方时，

如图2，连接OP

同理可得：△OPC≌△BPD（AAS），

所以OC＝BD＝2，．

由直线y＝﹣x+7，可得B（7，0），

在Rt△OCD中，CD＝＝，

当点C在y轴下方时，

如图3，连接OP

同理可得△OPC≌△BPD（AAS）；

所以CO＝BD＝2，．

由B（7，0），可得OD＝9，

在Rt△OCD中，CD＝＝；

综上所述，CD的长度为或