八年级（上）期末数学试卷

这是一份八年级（上）期末数学试卷，共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。


1. 函数y=2−x+1x−1中自变量x的取值范围是( )
A.x≤2B.x≤2且x≠1C.x<2且x≠1D.x≠1

2. 下列长度的三条线段，哪一组不能构成三角形( )
A.3，3，3B.3，4，5C.5，6，10D.4，5，9

3. 在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（ ）
A.B.C.D.

4. 一个多边形的内角和是外角和的2倍，这个多边形是（ ）
A.四边形B.五边形C.六边形D.八边形

5. 如图，每个小正方形的边长为1，△ABC的三边a、b、c的大小关系式正确的是（ ）
A.c
6.
如图，在△ABC中，AB=AC，且D为BC上一点，CD=AD，AB=BD，则∠B的度数为( )
A.30∘B.36∘C.40∘D.45∘

7. 如图，△ACB≅△A′CB′，∠BCB′=30∘，则∠ACA′的度数为( )

A.20∘B.30∘C.35∘D.40∘

8. 如图，在△ABC中，∠B＝42∘，AD⊥BC于点D，点E是BD上一点，EF⊥AB于点F，若ED＝EF，则∠AEC的度数为（ ）

A.60∘B.62∘C.64∘D.66∘

9. (2x)n−81分解因式后得(4x2+9)(2x+3)(2x−3)，则n等于（ ）
A.2B.4C.6D.8

10. 甲、乙两地之间的高速公路全长200千米，比原来国道的长度减少了20千米．高速公路通车后，某长途汽车的行驶速度提高了45千米/时，从甲地到乙地的行驶时间缩短了一半．设该长途汽车在原来国道上行驶的速度为x千米/时，根据题意，下列方程正确的是（ ）
A.200x=180x−45⋅12B.200x=220x−45⋅12
C.200x+45=180x⋅12D.200x+45=220x⋅12
二、填空题：每空3分，共18分．

若点A(m+2, 3)与点B(−4, n+5)关于y轴对称，则m+n=________．

当x=________时，2x−3与54x+3的值互为倒数．

如图，已知△ABC的三个内角的平分线交于点O，点D在CA的延长线上，且DC=BC，若∠BAC=80∘，则∠BOD的度数为________．


分解因式：(x2+4)2−16x2=________．

如图，在五边形ABCDE中，∠A+∠B+∠E＝300∘，DP、CP分别平分∠EDC、∠BCD，则∠CPD的度数是________​∘．


如图，∠BAC=110∘，若MP和NQ分别垂直平分AB和AC，则∠PAQ的度数是________．

三、解答题：第17-21题各8分，第22-23题各10分，第24题12分，共72分。

（1）x−33x2−6x÷(x+2−5x−2)；
(2)(−2a2)2⋅a4−(−5a4)2．

解分式方程：
（1）2yy−1+1=3y−1y；

（2）xx2−4−1x−2=−2x+2．

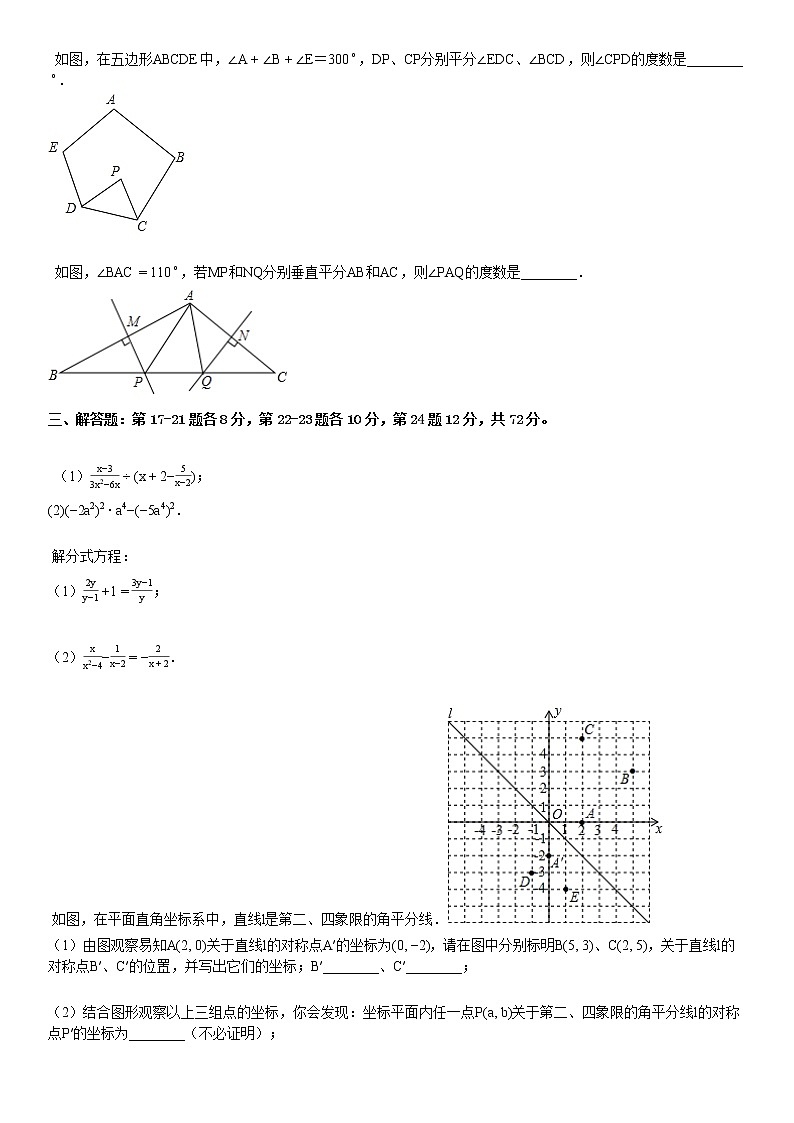
如图，在平面直角坐标系中，直线l是第二、四象限的角平分线．
（1）由图观察易知A(2, 0)关于直线l的对称点A′的坐标为(0, −2)，请在图中分别标明B(5, 3)、C(2, 5)，关于直线l的对称点B′、C′的位置，并写出它们的坐标；B′________、C′________；

（2）结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点P(a, b)关于第二、四象限的角平分线l的对称点P′的坐标为________（不必证明）；

（3）已知两点D(−1, −3)、E(1, −4)，试在直线l上确定一点Q，使点Q到D、E两点的距离之和最小，并求出Q点坐标．

如图，在△ABC中，AB=AC，点D，E，F分别在边AB，BC，AC上，且BD=CE，BE=CF，如果点G为DF的中点，那么EG与DF垂直吗？

先阅读下列材料：
我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法，其实分解因式的方法还有分组分解法、拆项法、十字相乘法等等．
（1）分组分解法：将一个多项式适当分组后，可提公因式或运用公式继续分解的方法．
如：ax+by+bx+ay=(ax+bx)+(ay+by)
=x(a+b)+y(a+b)
=(a+b)(x+y)
2xy+y2−1+x2
=x2+2xy+y2−1
=(x+y)2−1
=(x+y+1)(x+y−1)

（2）拆项法：将一个多项式的某一项拆成两项后，可提公因式或运用公式继续分解的方法．如：
x2+2x−3
=x2+2x+1−4
=(x+1)2−22
=(x+1+2)(x+1−2)
=(x+3)(x−1)
请你仿照以上方法，探索并解决下列问题：
（1）分解因式：a2−b2+a−b；
（2）分解因式：x2−6x−7；

（3）分解因式：a2+4ab−5b2．

如图所示，△ABC中，AB=BC，DE⊥AB于点E，DF⊥BC于点D，交AC于F.

(1)若∠AFD=155∘，求∠EDF的度数；

(2)若点F是AC的中点，求证：∠CFD=12∠B．

某文具店老板第一次用1000元购进一批文具，很快销售完毕；第二次购进时发现每件文具进价比第一次上涨了2.5元．老板用2500元购进了第二批文具，所购进文具的数量是第一次购进数量的2倍，同样很快销售完毕，两批文具的售价为每件15元．
（1）问第二次购进了多少件文具？

（2）文具店老板第一次购进的文具有30元的损耗，第二次购进的文具有125元的损耗，问文具店老板在这两笔生意中是盈利还是亏本？请说明理由．

已知，点D位直线BC上一动点（点D不与点B，C重合），∠BAC=90∘，AB=AC，∠ABC=∠ACB=45∘，∠DAE=90∘，AD=AE，连接CE．
（1）如图1，当点D在线段BC上时，求证：
①BD⊥CE；
②CE=BC−CD．
知识迁移，探究发现

（2）如图2，当点D在线段BC的延长线上时，其他条件不变，请直接写出CE，BC，CD三条线段之间的数量关系．
参考答案与试题解析
2016-2017学年湖北省鄂州市鄂城区八年级（上）期末数学试卷
一、选择题：每空3分，共30分．
1.
【答案】
B
【考点】
函数自变量的取值范围
【解析】
根据二次根式的性质和分式的意义，被开方数大于等于0，分母不等于0，就可以求解．
【解答】
解：根据二次根式有意义，分式有意义得：2−x≥0且x−1≠0，
解得：x≤2且x≠1．
故选B.
2.
【答案】
D
【考点】
三角形三边关系
【解析】
先回顾一下三角形的三边关系定理，根据判定定理逐个判断即可．
【解答】
解：A，3+3>3，符合三角形的三边关系定理，故本选项错误；
B，3+4>5，3+5>4，5+4>3，符合三角形的三边关系定理，故本选项错误；
C，5+6>10，5+10>6，6+10>5，符合三角形的三边关系定理，故本选项错误；
D，4+5=9，不符合三角形的三边关系定理，故本选项正确.
故选D．
3.
【答案】
A
【考点】
轴对称图形
【解析】
根据轴对称图形的概念求解．如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴．
【解答】
解：观察图形可知，
A、是轴对称图形，故A符合题意；
B、不是轴对称图形，故B不符合题意；
C、不是轴对称图形，故C不符合题意；
D、不是轴对称图形，故D不符合题意．
故选A.
4.
【答案】
C
【考点】
多边形内角与外角
【解析】
此题可以利用多边形的外角和和内角和定理求解．
【解答】
解：设所求多边形边数为n，
由题意得：
(n−2)⋅180∘=360∘×2，
解得n=6．
则这个多边形是六边形．
故选C.
5.
【答案】
A
【考点】
勾股定理
【解析】
通过小正方形网格，可以看出AB=4，AC、BC分别可以构造直角三角形，再利用勾股定理可分别求出b、a，然后比较三边的大小即可．
【解答】
解：∵ b=AC=42+32=5=25，a=BC=42+12=17，c=4=16，
∴ b>a>c，
即c故选A．
6.
【答案】
B
【考点】
等腰三角形的判定与性质
【解析】
求出∠BAD=2∠CAD=2∠B=2∠C的关系，利用三角形的内角和是180∘，求∠B，
【解答】
解：∵ AB=AC，
∴ ∠B=∠C，
∵ AB=BD，
∴ ∠BAD=∠BDA，
∵ CD=AD，
∴ ∠C=∠CAD，
∵ ∠BAD+∠CAD+∠B+∠C=180∘，
∴ 5∠B=180∘，
∴ ∠B=36∘.
故选B.
7.
【答案】
B
【考点】
全等三角形的性质
【解析】
本题根据全等三角形的性质并找清全等三角形的对应角即可．
【解答】
解：∵ △ACB≅△A′CB′，
∴ ∠ACB=∠A′CB′，
即∠ACA′+∠A′CB=∠B′CB+∠A′CB，
∴ ∠ACA′=∠B′CB，
又∠B′CB=30∘
∴ ∠ACA′=30∘．
故选B．
8.
【答案】
D
【考点】
角平分线的性质
【解析】
根据三角形内角和定理求出∠BAD，根据角平分线的判定定理得到∠BAE＝∠DAE，根据三角形的外角的性质计算即可．
【解答】
∵ ∠B＝42∘，AD⊥BC，
∴ ∠BAD＝48∘，
∵ ED＝EF，AD⊥BC，EF⊥AB，
∴ ∠BAE＝∠DAE＝24∘，
∴ ∠AEC＝∠B+∠BAE＝66∘，
9.
【答案】
B
【考点】
因式分解-运用公式法
【解析】
直接利用平方差公式计算得出答案．
【解答】
解：∵ (4x2+9)(2x+3)(2x−3)
=(4x2+9)(4x2−9)
=16x4−81
=(2x)4−81
=(2x)n−81，
∴ n=4．
故选：B．
10.
【答案】
D
【考点】
由实际问题抽象为分式方程
【解析】
设该长途汽车在原来国道上行驶的速度为x千米/时，根据“甲、乙两地之间的高速公路全长200千米，比原来国道的长度减少了20千米．高速公路通车后，某长途汽车的行驶速度提高了45千米/时，从甲地到乙地的行驶时间缩短了一半”，可列出方程．
【解答】
解：设该长途汽车在原来国道上行驶的速度为x千米/时，
根据题意得
200x+45=220x⋅12．
故选D．
二、填空题：每空3分，共18分．
【答案】
0
【考点】
关于x轴、y轴对称的点的坐标
【解析】
根据“关于y轴对称的点，纵坐标相同，横坐标互为相反数”列出方程求解即可．
【解答】
解：∵ 点A(m+2, 3)与点B(−4, n+5)关于y轴对称，
∴ m+2=4，3=n+5，
解得：m=2，n=−2，
∴ m+n=0，
故答案为：0．
【答案】
3
【考点】
解一元一次方程
【解析】
首先根据倒数的定义列出方程2x−3=4x+35，然后解方程即可．
【解答】
解：∵ 2x−3与54x+3的值互为倒数，
∴ 2x−3=4x+35，
去分母得：5(2x−3)=4x+3，
去括号得：10x−15=4x+3，
移项、合并得：6x=18，
系数化为1得：x=3．
所以当x=3时，2x−3与54x+3的值互为倒数．
【答案】
100∘
【考点】
全等三角形的性质
【解析】
如图在CO的延长线上取一点H．首先证明∠DOB=∠D+∠OBC+∠OCD+∠OCB=∠D+∠OBC+∠ACB，由△OCD≅△OCB，推出∠D=∠OBC=∠ABO，推出∠DOB=∠ABC+∠ACB=180∘−∠BAC，延长即可解决问题．
【解答】
解：如图在CO的延长线上取一点H．
∵ ∠DOH=∠D+∠DCO，∠BOH=∠OBC+∠OCB，
∴ ∠DOB=∠D+∠OBC+∠OCD+∠OCB=∠D+∠OBC+∠ACB，
∵ O是内心，
∴ ∠DCO=∠BCO，
在△OCD和△OCB中，
OC=OC∠OCD=∠OCBCD=CB，
∴ △OCD≅△OCB(SAS)，
∴ ∠D=∠OBC=∠ABO，
∴ ∠DOB=∠ABC+∠ACB=180∘−∠BAC=100∘，
故答案为：100∘．
【答案】
(x+2)2(x−2)2
【考点】
因式分解-运用公式法
【解析】
先利用平方差公式分解，再利用完全平方公式进行二次因式分解．
【解答】
解：(x2+4)2−16x2
=(x2+4−4x)(x2+4+4x)
=(x+2)2(x−2)2．
故答案为：(x+2)2(x−2)2.
【答案】
60
【考点】
多边形内角与外角
三角形内角和定理
角平分线的性质
【解析】
根据五边形的内角和等于540∘，由∠A+∠B+∠E＝300∘，可求∠BCD+∠CDE的度数，再根据角平分线的定义可得∠PDC与∠PCD的角度和，进一步求得∠CPD的度数．
【解答】
∵ 五边形的内角和等于540∘，∠A+∠B+∠E＝300∘，
∴ ∠BCD+∠CDE＝540∘−300∘＝240∘，
∵ ∠BCD、∠CDE的平分线在五边形内相交于点O，
∴ ∠PDC+∠PCD=12(∠BCD+∠CDE)＝120∘，
∴ ∠CPD＝180∘−120∘＝60∘．
【答案】
40∘
【考点】
线段垂直平分线的性质
【解析】
根据三角形内角和定理求出∠B+∠C的度数，根据线段的垂直平分线的性质得到PA=PB，QA=QC，得到∠PAB=∠B，∠QAC=∠C，结合图形计算即可．
【解答】
解：∵ ∠BAC=110∘，
∴ ∠B+∠C=70∘，
∵ MP和NQ分别垂直平分AB和AC，
∴ PA=PB，QA=QC，
∴ ∠PAB=∠B，∠QAC=∠C，
∴ ∠PAB+∠QAC=∠B+∠C=70∘，
∴ ∠PAQ=∠BAC−(∠PAB+∠QAC)=40∘，
故答案为：40∘．
三、解答题：第17-21题各8分，第22-23题各10分，第24题12分，共72分。
【答案】
解：（1）原式=x−33x(x−2)÷(x−2)(x+2)−5x−2
=x−33x(x−2)÷x2−9x−2
=x−33x(x−2)×x−2(x−3)(x+3)
=13x(x+3)
=13x2+9x．
（2）原式=4a4×a4−25a8
=4a8−25a8
=−21a8．
【考点】
分式的混合运算
单项式乘单项式
【解析】
结合分式混合运算的运算法则进行求解即可．
【解答】
解：（1）原式=x−33x(x−2)÷(x−2)(x+2)−5x−2
=x−33x(x−2)÷x2−9x−2
=x−33x(x−2)×x−2(x−3)(x+3)
=13x(x+3)
=13x2+9x．
（2）原式=4a4×a4−25a8
=4a8−25a8
=−21a8．
【答案】
解：（1）去分母得：2y2+y2−y=3y2−4y+1，
解得：y=13，
经检验y=13是分式方程的解；
（2）去分母得：x−x−2=−2x+4，
解得：x=3，
经检验x=3是分式方程的解．
【考点】
解分式方程
【解析】
两分式方程去分母转化为整式方程，求出整式方程的解得到未知数的值，代入检验即可．
【解答】
解：（1）去分母得：2y2+y2−y=3y2−4y+1，
解得：y=13，
经检验y=13是分式方程的解；
（2）去分母得：x−x−2=−2x+4，
解得：x=3，
经检验x=3是分式方程的解．
【答案】
(−3, −5),(−5, −2)
(−b, −a)
【考点】
轴对称——最短路线问题
坐标与图形变化-对称
【解析】
（1）分别作B(5, 3)、C(2, 5)关于直线l的对称点B′，C′，B′(−3, −5)、C′(−5, −2)；
（2）观察以上三组点的坐标，会发现坐标平面内任一点P(a, b)关于第二、四象限的角平分线l的对称点P′的坐标为(−b, −a)；
（3）先求出点D关于直线l的对称点D′的坐标为(3, 1)，再运用待定系数法求出点E、点D′的直线解析式为y=52x−132．点Q是直线y=52x−132与直线l:y=−x的交点，解方程组：y=52x−132y=−x，即可得到点Q的坐标．
【解答】
解：（1）如图：B′(−3, −5)、C′(−5, −2)；
（2）∵ A(2, 0)关于直线l的对称点A′的坐标为(0, −2)，
B(5, 3)关于直线l的对称点B′(−3, −5)，
C(2, 5)关于直线l的对称点C′(−5, −2)，
∴ 发现：坐标平面内任一点P(a, b)关于第二、四象限的角平分线l的对称点P′的坐标为(−b, −a)；
（3）点D关于直线l的对称点D′的坐标为(3, 1)．
设过点E、点D′的直线解析式为：y=kx+b，
分别把点E、D′的坐标代入得k+b=−43k+b=1，
解得k=52b=−132，
∴ y=52x−132．
解方程组：y=52x−132y=−x，
得x=137y=−137，
∴ 点Q的坐标为(137, −137)．
【答案】
解：连接DE，EF，
∵ AB=AC，
∴ ∠B=∠C，
在△BDE和△CFE中，
BD=CE∠B=∠CBE=CF，
∴ △BDE≅△CFE(SAS)，
∴ DE=EF，
在在△DGE和△FGE中，
DG=FGGE=GEDE=EF，
∴ △DGE≅△FGE(SSS)，
∴ ∠DGE=∠FGE，
∵ ∠DGE+∠FGE=180∘，
∴ ∠DGE=∠FGE=90∘，
∴ EG⊥DF．
【考点】
全等三角形的性质
等腰三角形的判定与性质
【解析】
连接DE，EF，易证△BDE≅△CFE，可得DE=EF，可证△DGE≅△FGE，可求得∠DGE=∠FGE=90∘．
【解答】
解：连接DE，EF，
∵ AB=AC，
∴ ∠B=∠C，
在△BDE和△CFE中，
BD=CE∠B=∠CBE=CF，
∴ △BDE≅△CFE(SAS)，
∴ DE=EF，
在在△DGE和△FGE中，
DG=FGGE=GEDE=EF，
∴ △DGE≅△FGE(SSS)，
∴ ∠DGE=∠FGE，
∵ ∠DGE+∠FGE=180∘，
∴ ∠DGE=∠FGE=90∘，
∴ EG⊥DF．
【答案】
解：（1）原式=(a+b)(a−b)+(a−b)=(a−b)(a+b+1)；
（2）原式=(x−7)(x+1)；
（3）原式=(a−b)(a+5b)．
【考点】
因式分解-十字相乘法
【解析】
仿照题中的方法，得到十字相乘法的技巧，分别将各项分解即可．
【解答】
解：（1）原式=(a+b)(a−b)+(a−b)=(a−b)(a+b+1)；
（2）原式=(x−7)(x+1)；
（3）原式=(a−b)(a+5b)．
【答案】
(1)解：∵ ∠AFD=155∘，
∴ ∠DFC=25∘.
∵ DF⊥BC，DE⊥AB，
∴ ∠FDC=∠AED=90∘.
在Rt△FDC中，
∴ ∠C=90∘−25∘=65∘.
∵ AB=BC，
∴ ∠C=∠A=65∘，
∴ ∠EDF=360∘−65∘−155∘−90∘=50∘；
(2)证明：连接BF，
∵ AB=BC，且点F是AC的中点，
∴ BF⊥AC，∠ABF=∠CBF=12∠ABC，
∴ ∠CFD+∠BFD=90∘，
∠CBF+∠BFD=90∘，
∴ ∠CFD=∠CBF，
∴ ∠CFD=12∠ABC.
【考点】
等腰三角形的性质：三线合一
三角形内角和定理
等腰三角形的性质
【解析】
（1）求得∠A的度数后利用四边形的内角和定理求得结论即可；
（2）连接FB，根据AB=BC，且点F是AC的中点，得到BF⊥AC，∠ABF=∠CBF=12∠ABC，证得∠CFD=∠CBF后即可证得∠CFD=12∠ABC．
【解答】
(1)解：∵ ∠AFD=155∘，
∴ ∠DFC=25∘.
∵ DF⊥BC，DE⊥AB，
∴ ∠FDC=∠AED=90∘.
在Rt△FDC中，
∴ ∠C=90∘−25∘=65∘.
∵ AB=BC，
∴ ∠C=∠A=65∘，
∴ ∠EDF=360∘−65∘−155∘−90∘=50∘；
(2)证明：连接BF，
∵ AB=BC，且点F是AC的中点，
∴ BF⊥AC，∠ABF=∠CBF=12∠ABC，
∴ ∠CFD+∠BFD=90∘，
∠CBF+∠BFD=90∘，
∴ ∠CFD=∠CBF，
∴ ∠CFD=12∠ABC.
【答案】
第二次购进200件文具；
（2）第一次购进100件文具，利润为：(15−10)×100−30=470（元）；
第二次购进200件文具，利润为：(15−12.5)×200−125=375（元），
两笔生意是盈利：利润为470+375=845元．
【考点】
分式方程的应用
【解析】
（1）设第一次购进x件文具，第二次就购进2x件文具，根据第二次购进时发现每件文具进价比第一次上涨了2.5元，列分式方程求解；
（2）分别求出两次销售的利润，即可判断盈亏．
【解答】
解：（1）设第一次购进x件文具，第二次就购进2x件文具，
由题意得，1000x=25002x−2.5，
解得：x=100，
经检验，x=100是原方程的解，且符合题意，
则2x=2×100=200．
答：第二次购进200件文具；
（2）第一次购进100件文具，利润为：(15−10)×100−30=470（元）；
第二次购进200件文具，利润为：(15−12.5)×200−125=375（元），
两笔生意是盈利：利润为470+375=845元．
【答案】
（1）证明：如图1中，∵ ∠BAC=∠DAE=90∘，
∴ ∠BAD=∠CAE，
在△ABD和△ACE中，
AB=AC∠BAD=∠CAEAD=AE，
∴ △ABD≅△ACE(SAS)，
∴ ∠ABD=∠ACE=45∘，BD=CE，
∴ ∠ACB+∠ACE=90∘
∴ ∠ECB=90∘，
∴ BD⊥CE，CE=BC−CD．
（2）如图2中，结论：CE=BC+CD，理由如下：
∵ ∠BAC=∠DAE=90∘，
∴ ∠BAD=∠CAE，
在△ABD和△ACE中，
AB=AC∠BAD=∠CAEAD=AE，
∴ △ABD≅△ACE(SAS)，
∴ BD=CE，
∴ CE=BC+CD．
【考点】
三角形综合题
【解析】
（1）如图1中，只要证明△ABD≅△ACE，即可得到∠ABD=∠ACE=45∘，BD=CE，由此可以证明．
（2）如图2中，结论：CE=BC+CD，证明方法类似（1）．
【解答】
（1）证明：如图1中，∵ ∠BAC=∠DAE=90∘，
∴ ∠BAD=∠CAE，
在△ABD和△ACE中，
AB=AC∠BAD=∠CAEAD=AE，
∴ △ABD≅△ACE(SAS)，
∴ ∠ABD=∠ACE=45∘，BD=CE，
∴ ∠ACB+∠ACE=90∘
∴ ∠ECB=90∘，
∴ BD⊥CE，CE=BC−CD．
（2）如图2中，结论：CE=BC+CD，理由如下：
∵ ∠BAC=∠DAE=90∘，
∴ ∠BAD=∠CAE，
在△ABD和△ACE中，
AB=AC∠BAD=∠CAEAD=AE，
∴ △ABD≅△ACE(SAS)，
∴ BD=CE，
∴ CE=BC+CD．