

某校八年级(上)期末数学模拟试卷1
展开1. 9的算术平方根是( )
A.3B.−3C.3D.81
2. 在下列长度的各组线段中,能组成直角三角形的是( )
A.5,6,7B.2,5,7C.1,4,9D.5,11,12
3. 下列计算结果正确的是( )
A.(−3)2=3B.36=±6C.3+2=5D.3+23=53
4. 在平面直角坐标系中,将点P(−2, 3)沿x轴方向向右平移3个单位得到点Q,则点Q的坐标是( )
A.(−2, 6)B.(−2, 0)C.(−5, 3)D.(1, 3)
5. 已知点P(x+1, 2)关于x轴的对称点是点Q(−1, 2y),则2x+y的值是( )
A.3B.−3C.−5D.5
6. 如图,AB // CD,∠D=∠E=35∘,则∠B的度数为( )
A.60∘B.65∘C.70∘D.75∘
7. 一次函数y=kx−b,当k<0,b<0时的图象大致位置是( )
A.B.C.D.
8. 下列数据是2013年3月7日6点公布的中国六大城市的空气污染指数情况:
则这组数据的中位数和众数分别是( )
A.164和163B.105和163C.105和164D.163和164
9. 某班学生分组搞活动,若每组7人,则余下4人;若每组8人,则有一组少3人.设全班有学生x 人,分成y 个小组,则可得方程组( )
A.7x+4=y8x−3=yB.7y=x+48y+3=x
C.7y=x−48y=x+3D.7y=x+48y=x+3
10. 如果方程组x=4ax+by=5 的解与方程组y=3bx+ay=2 的解相同,则a+b的值为( )
A.−1B.2C.1D.0
11. 一次函数y1=kx+b与y2=x+a的图象如图,则下列结论①k<0;②a>0;③当x<3时,y1
A.0B.1C.2D.3
12. 已知一次函数y=kx+b(k≠0)图象过点(0, 2),且与两坐标轴围成的三角形面积为2,则一次函数的解析式为( )
A.y=x+2B.y=−x+2
C.y=x+2或y=−x+2D.y=−x+2或y=x−2
二、填空题(每题3分,共12分)
若2a3xby+5与5a2−4yb2x是同类项,则x=________,y=________.
如图,已知AB // CD,DA平分∠BDC,∠ADE=90∘,∠B=120∘,则∠BDE=________度.
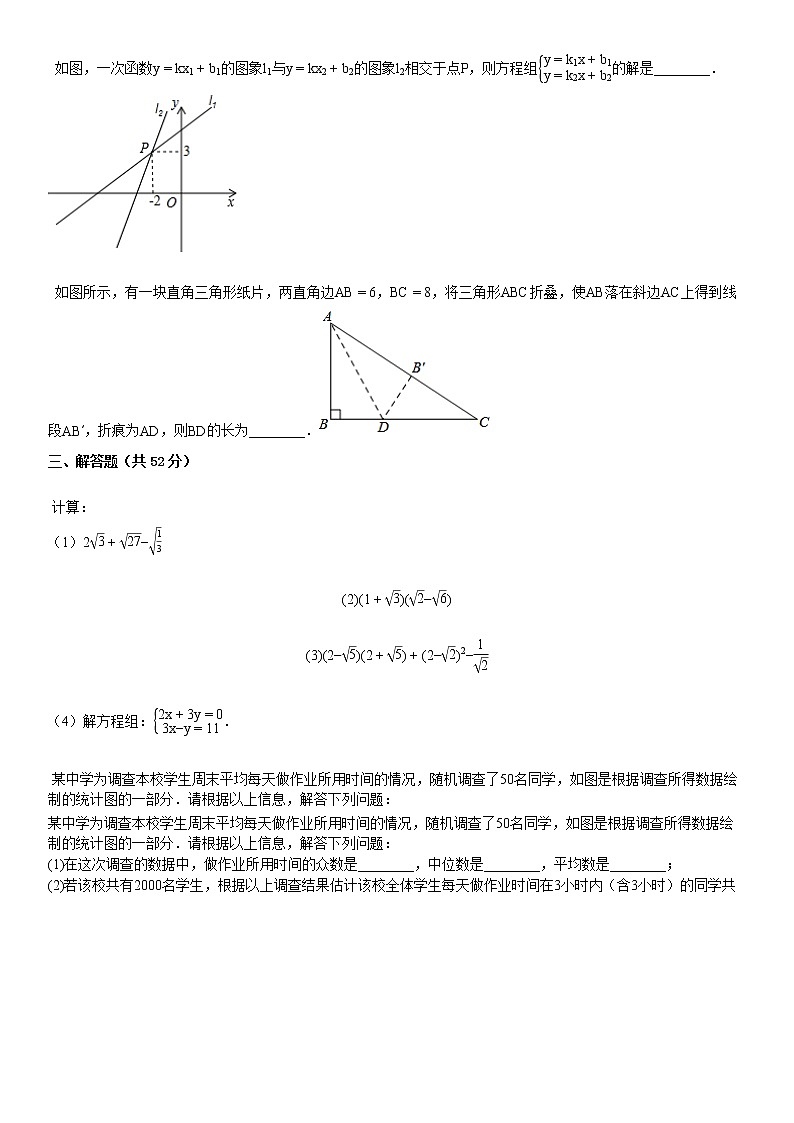
如图,一次函数y=kx1+b1的图象l1与y=kx2+b2的图象l2相交于点P,则方程组y=k1x+b1y=k2x+b2的解是________.
如图所示,有一块直角三角形纸片,两直角边AB=6,BC=8,将三角形ABC折叠,使AB落在斜边AC上得到线段AB′,折痕为AD,则BD的长为________.
三、解答题(共52分)
计算:
(1)23+27−13
(2)(1+3)(2−6)
(3)(2−5)(2+5)+(2−2)2−12
(4)解方程组:2x+3y=03x−y=11.
某中学为调查本校学生周末平均每天做作业所用时间的情况,随机调查了50名同学,如图是根据调查所得数据绘制的统计图的一部分.请根据以上信息,解答下列问题:
某中学为调查本校学生周末平均每天做作业所用时间的情况,随机调查了50名同学,如图是根据调查所得数据绘制的统计图的一部分.请根据以上信息,解答下列问题:
(1)在这次调查的数据中,做作业所用时间的众数是________,中位数是________,平均数是________;
(2)若该校共有2000名学生,根据以上调查结果估计该校全体学生每天做作业时间在3小时内(含3小时)的同学共有多少人?
如图,四边形ABCD是正方形,E、F分别是AB和BC延长线上的点,且AE=CF.
(1)求证:△ADE≅△CDF;
(2)连接EF,若AB=3,AE=1,求EF的长.
阅读下列解题过程:
12+1=2−1(2+1)(2−1)=2−1
13+2=3−2(3+2)(3−2)=3−2
14+3=4−3(4+3)(4−3)=4−3;
…
则:
(1)110+9=________;1100+99=________;
(2)观察上面的解题过程,请直接写出式子1n−n−1=________;
(3)利用这一规律计算:(12+1+13+2+14+3+...+12009+2008)(2009+1)的值.
已知:用2辆A型车和1辆B型车载满货物一次可运货10吨;用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物.
根据以上信息,解答下列问题:
(1)1辆A型车和1辆车B型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费.
如图,已知函数y=−12x+b的图象与x轴、y轴分别交于点A,B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P(a, 0)(其中a>2),过点P作x轴的垂线,分别交函数y=−12x+b和y=x的图象于点C,D.
(1)求点A的坐标;
(2)若OB=CD,求a的值.
参考答案与试题解析
2016-2017学年湖北省恩施州利川市某校八年级(上)期末数学模拟试卷
一、选择题(每题3分,共36分)
1.
【答案】
C
【考点】
算术平方根
【解析】
先根据算术平方根的定义求出9=3,再根据算术平方根的定义解答即可.
【解答】
解:∵ 9=3,
∴ 9的算术平方根是3.
故选C.
2.
【答案】
B
【考点】
勾股定理的逆定理
【解析】
欲求证是否为直角三角形,这里给出三边的长,只要验证两小边的平方和等于最长边的平方即可.
【解答】
解:A、因为52+62≠72,所以不能组成直角三角形;
B、因为(2)2+(5)2=(7)2,所以能组成直角三角形;
C、因为12+42≠92,所以不能组成直角三角形;
D、因为52+112≠122,所以不能组成直角三角形.
故选B.
3.
【答案】
A
【考点】
实数的运算
【解析】
将四个选项分别进行计算,即可判断出正确结果.
【解答】
解:A、∵ (−3)2=9=3,故本选项正确;
B、∵ 36表示36的算术平方根,∴ 36=6,故本选项错误;
C、∵ 3和2不是同类二次根式,∴ 不能合并,故本选项错误;
D、∵ 3和23不是同类二次根式,∴ 不能合并,故本选项错误;
故选A.
4.
【答案】
D
【考点】
坐标与图形变化-平移
轨迹
【解析】
直接利用平移中点的变化规律求解即可.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
【解答】
解:将点P(−2, 3)向右平移3个单位到Q点,
即Q点的横坐标加3,纵坐标不变,即Q点的坐标为(1, 3),
故选D.
5.
【答案】
C
【考点】
关于x轴、y轴对称的点的坐标
【解析】
利用平面内两点关于x轴对称时:横坐标不变,纵坐标互为相反数,进行求解.
【解答】
解:点P(x+1, 2)关于x轴的对称点是点Q(−1, 2y),得
x+1=−1,2y+2=0,
解得x=−2,y=−1
则2x+y=2×(−2)+(−1)=−5,
故选:C.
6.
【答案】
C
【考点】
平行线的判定与性质
三角形的外角性质
【解析】
根据 三角形的一个外角等于与它不相邻的两个内角的和求出∠1,再根据两直线平行,同位角相等解答.
【解答】
解:∵ ∠D=∠E=35∘,
∴ ∠1=∠D+∠E=35∘+35∘=70∘,
∵ AB // CD,
∴ ∠B=∠1=70∘.
故选C.
7.
【答案】
C
【考点】
一次函数图象与系数的关系
【解析】
先根据k<0,b<0判断出一次函数y=kx−b的图象经过的象限,进而可得出结论.
【解答】
解:∵ 一次函数y=kx−b,k<0,b<0,
∴ −b>0,
∴ 函数图象经过一二四象限,
故选C.
8.
【答案】
A
【考点】
中位数
众数
【解析】
根据众数定义:一组数据中出现次数最多的数据叫做众数.中位数:将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.可以直接算出答案.
【解答】
把数据从小到大排列:45,163,163,165,227,342,位置处于中间的数是163和165,故中位数是(163+165)÷2=164,
163出现了两次,故众数是163;
9.
【答案】
C
【考点】
由实际问题抽象出二元一次方程组
【解析】
此题中的关键性的信息是:①若每组7人,则余下4人;②若每组8人,则有一组少3人.
【解答】
解:根据若每组7人,则余下4人,得方程7y=x−4;
根据若每组8人,则有一组少3人,得方程8y=x+3.
可列方程组为7y=x−4,8y=x+3.
故选C.
10.
【答案】
C
【考点】
二元一次方程组的解
【解析】
把x=4y=3 代入方程组ax+by=5bx+ay=2 ,得到一个关于a,b的方程组,将方程组的两个方程左右两边分别相加,整理即可得出a+b的值.
【解答】
把x=4y=3 代入方程组ax+by=5bx+ay=2 ,
得4a+3b=54b+3a=2 ,
①+②,得:7(a+b)=7,
则a+b=1,
11.
【答案】
B
【考点】
一次函数图象与系数的关系
【解析】
根据y1=kx+b和y2=x+a的图象可知:k<0,a<0,所以当x<3时,相应的x的值,y1图象均高于y2的图象.
【解答】
解:∵ y1=kx+b的函数值随x的增大而减小,
∴ k<0,故①正确;
∵ y2=x+a的图象与y轴交于负半轴,
∴ a<0,故②错误;
∵ 当x<3时,相应的x的值,y1图象均高于y2的图象,
∴ y1>y2,故③错误.
故选B.
12.
【答案】
C
【考点】
待定系数法求一次函数解析式
【解析】
先求出一次函数y=kx+b与x轴和y轴的交点,再利用三角形的面积公式得到关于k的方程,解方程即可求出k的值.
【解答】
解:∵ 一次函数y=kx+b(k≠0)图象过点(0, 2),
∴ b=2,
令y=0,则x=−2k,
∵ 函数图象与两坐标轴围成的三角形面积为2,
∴ 12×2×|−2k|=2,即|2k|=2,
解得:k=±1,
则函数的解析式是y=x+2或y=−x+2.
故选:C.
二、填空题(每题3分,共12分)
【答案】
2,−1
【考点】
同类项的概念
【解析】
根据同类项的定义(所含字母相同,相同字母的指数相同)列出方程,求出x,y的值.
【解答】
解:根据题意得:3x=2−4y,y+5=2x,
解得:x=2,y=−1.
故答案为:2;−1.
【答案】
120
【考点】
平行线的判定与性质
【解析】
由DA为角平分线得到一对角相等,再由AB与CD平行得到一对内错角相等,等量代换得到∠A=∠ADB,根据∠B的度数求出∠ADB的度数,即为∠ADC的度数,根据∠ADE为直角,即可确定出∠BDE的度数.
【解答】
解:∵ DA平分∠BDC,
∴ ∠ADB=∠ADC,
∵ AB // CD,
∴ ∠A=∠ADC,
∵ ∠B=120∘,
∴ ∠A=∠ADC=∠ADB=30∘,
∵ ∠ADE=90∘,
∴ ∠BDE=∠ADE+∠ADB=90∘+30∘=120∘.
故答案为:120
【答案】
x=−2y=3
【考点】
一次函数与二元一次方程(组)
【解析】
根据二元一次方程组的解即为两直线的交点坐标解答.
【解答】
解:由图可知,方程组y=k1x+b1y=k2x+b2的解是x=−2y=3.
故答案为:x=−2y=3.
【答案】
3
【考点】
翻折变换(折叠问题)
【解析】
设点B落在AC上的E点处,连接DE,如图所示,由三角形ABC为直角三角形,由AB与BC的长,利用勾股定理求出AC的长,设BD=x,由折叠的性质得到ED=BD=x,AE=AB=6,进而表示出CE与CD,在直角三角形DEC中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即可确定出BD的长.
【解答】
解:∵ △ABC为直角三角形,AB=6,BC=8,
∴ 根据勾股定理得:AC=AB2+BC2=10,
设BD=x,由折叠可知:DB′=BD=x,AB′=AB=6,
可得:CB′=AC−AB′=10−6=4,CD=BC−BD=8−x,
在Rt△CDB′中,
根据勾股定理得:(8−x)2=42+x2,
解得:x=3,
则BD=3.
故答案为:3.
三、解答题(共52分)
【答案】
解:(1)原式=23+33−33
=1433;
(2)原式=2(1+3)(1−3)
=2×(1−3)
=−22;
(3)原式=4−5+4−42+2−22
=5−922;
(4)2x+3y=0①3x−y=11②,
①+②×3得11x=33,解得x=3,
把x=3代入①得6+3y=0,解得y=−2,
所以方程组的解为x=3y=−2.
【考点】
二次根式的混合运算
代入消元法解二元一次方程组
【解析】
(1)先把各二次根式化简为最简二次根式,然后合并即可;
(2)把后面的括号内提2,然后利用平方差公式计算;
(3)先利用平方差公式和完全平方公式计算,然后合并即可;
(4)利用加减消元法解方程组.
【解答】
解:(1)原式=23+33−33
=1433;
(2)原式=2(1+3)(1−3)
=2×(1−3)
=−22;
(3)原式=4−5+4−42+2−22
=5−922;
(4)2x+3y=0①3x−y=11②,
①+②×3得11x=33,解得x=3,
把x=3代入①得6+3y=0,解得y=−2,
所以方程组的解为x=3y=−2.
【答案】
3,3,3
【考点】
条形统计图
用样本估计总体
加权平均数
中位数
众数
【解析】
据圆周角定得到∠ACB=9,∠A=∠=40∘然后利利用互余计算∠ABC.
【解答】
解:AB为直径,
∠AB=90∘,
∵ ∠A=∠DC=4∘,
故答为50.
【答案】
解:(1)∵ 正方形ABCD中,∠A=∠BCD=90∘,则
∠DCF=∠A=90∘,AD=CD,
在△ADE和△CDF中,
AD=CD∠A=∠DCFAE=CF,
∴ △ADE≅△CDF(SAS);
(2)∵ AB=BC=3,CF=AE=1,
∴ BE=3−1=2,BF=3+1=4,
∴ Rt△BEF中,EF=22+42=20=25.
【考点】
正方形的性质
全等三角形的判定
勾股定理
【解析】
(1)根据两边及其夹角分别对应相等的两个三角形全等进行证明即可;
(2)先求得BE=3−1=2,BF=3+1=4,再根据勾股定理,在Rt△BEF中,求得EF即可.
【解答】
解:(1)∵ 正方形ABCD中,∠A=∠BCD=90∘,则
∠DCF=∠A=90∘,AD=CD,
在△ADE和△CDF中,
AD=CD∠A=∠DCFAE=CF,
∴ △ADE≅△CDF(SAS);
(2)∵ AB=BC=3,CF=AE=1,
∴ BE=3−1=2,BF=3+1=4,
∴ Rt△BEF中,EF=22+42=20=25.
【答案】
10−3,10−311
n+n−1
(3)原式=(2−1+3−2+4−3+...+2009−2008)(2009+1)
=(2009−1)(2009+1)
=2009−1
=2008.
【考点】
分母有理化
【解析】
(1)先分母有理化,再求出即可.
(2)根据已知的算式的结果得出即可.
(3)先根据已知得出(2−1+3−2+4−3+...+2009−2008)(2009+1),合并后根据平方差公式求出即可.
【解答】
解:(1)110+9=10−9(10+9)(10−9)=10−9=10−3,
1100+99=100−99(100+99)(100−99)=100−99=10−311
(2)1n−n−1=n+n−1,
(3)原式=(2−1+3−2+4−3+...+2009−2008)(2009+1)
=(2009−1)(2009+1)
=2009−1
=2008.
【答案】
解:(1)设每辆A型车、B型车都装满货物一次可以分别运货x吨、y吨,
依题意列方程组得:
2x+y=10,x+2y=11,
解方程组,得:x=3,y=4,
答:1辆A型车装满货物一次可运3吨,1辆B型车装满货物一次可运4吨.
(2)设租用A型车a辆,B型车b辆,
结合题意和(1)得:3a+4b=31,
∴ a=31−4b3,
∵ a,b都是正整数,
∴ a=9,b=1或a=5,b=4或a=1,b=7,
答:有3种租车方案:
方案一:A型车9辆,B型车1辆;
方案二:A型车5辆,B型车4辆;
方案三:A型车1辆,B型车7辆.
(3)∵ A型车每辆需租金100元/次,B型车每辆需租金120元/次,
∴ 方案一需租金:9×100+1×120=1020(元),
方案二需租金:5×100+4×120=980(元),
方案三需租金:1×100+7×120=940(元),
∵ 1020>980>940,
∴ 最省钱的租车方案是方案三:A型车1辆,B型车7辆,最少租车费为940元.
【考点】
二元一次方程组的应用——优化方案问题
二元一次方程组的应用——产品配套问题
【解析】
(1)根据“用2辆A型车和1辆B型车载满货物一次可运货10吨;”“用1辆A型车和2辆B型车载满货物一次可运货11吨”,分别得出等式方程,组成方程组求出即可;
(2)由题意理解出:3a+4b=31,解此二元一次方程,求出其整数解,得到三种租车方案;
(3)根据(2)中所求方案,利用A型车每辆需租金100元/次,B型车每辆需租金120元/次,分别求出租车费用即可.
【解答】
解:(1)设每辆A型车、B型车都装满货物一次可以分别运货x吨、y吨,
依题意列方程组得:
2x+y=10,x+2y=11,
解方程组,得:x=3,y=4,
答:1辆A型车装满货物一次可运3吨,1辆B型车装满货物一次可运4吨.
(2)设租用A型车a辆,B型车b辆,
结合题意和(1)得:3a+4b=31,
∴ a=31−4b3,
∵ a,b都是正整数,
∴ a=9,b=1或a=5,b=4或a=1,b=7,
答:有3种租车方案:
方案一:A型车9辆,B型车1辆;
方案二:A型车5辆,B型车4辆;
方案三:A型车1辆,B型车7辆.
(3)∵ A型车每辆需租金100元/次,B型车每辆需租金120元/次,
∴ 方案一需租金:9×100+1×120=1020(元),
方案二需租金:5×100+4×120=980(元),
方案三需租金:1×100+7×120=940(元),
∵ 1020>980>940,
∴ 最省钱的租车方案是方案三:A型车1辆,B型车7辆,最少租车费为940元.
【答案】
解:(1)∵ 点M在直线y=x的图象上,且点M的横坐标为2,
∴ 点M的坐标为(2, 2),
把M(2, 2)代入y=−12x+b得−1+b=2,解得b=3,
∴ 一次函数的解析式为y=−12x+3,
把y=0代入y=−12x+3得−12x+3=0,解得x=6,
∴ A点坐标为(6, 0);
(2)把x=0代入y=−12x+3得y=3,
∴ B点坐标为(0, 3),
∵ CD=OB,
∴ CD=3,
∵ PC⊥x轴,
∴ C点坐标为(a, −12a+3),D点坐标为(a, a)
∴ a−(−12a+3)=3,
∴ a=4.
【考点】
两直线垂直问题
两直线相交非垂直问题
【解析】
(1)先利用直线y=x上的点的坐标特征得到点M的坐标为(2, 2),再把M(2, 2)代入y=−12x+b可计算出b=3,得到一次函数的解析式为y=−12x+3,然后根据x轴上点的坐标特征可确定A点坐标为(6, 0);
(2)先确定B点坐标为(0, 3),则OB=CD=3,再表示出C点坐标为(a, −12a+3),D点坐标为(a, a),所以a−(−12a+3)=3,然后解方程即可.
【解答】
解:(1)∵ 点M在直线y=x的图象上,且点M的横坐标为2,
∴ 点M的坐标为(2, 2),
把M(2, 2)代入y=−12x+b得−1+b=2,解得b=3,
∴ 一次函数的解析式为y=−12x+3,
把y=0代入y=−12x+3得−12x+3=0,解得x=6,
∴ A点坐标为(6, 0);
(2)把x=0代入y=−12x+3得y=3,
∴ B点坐标为(0, 3),
∵ CD=OB,
∴ CD=3,
∵ PC⊥x轴,
∴ C点坐标为(a, −12a+3),D点坐标为(a, a)
∴ a−(−12a+3)=3,
∴ a=4.城市
北京
合肥
南京
哈尔滨
成都
南昌
污染指数
342
163
165
45
227
163
2023年安徽省合肥市某校中考数学模拟试卷(1)(含解析): 这是一份2023年安徽省合肥市某校中考数学模拟试卷(1)(含解析),共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
某校七年级(上)期末试卷(7): 这是一份某校七年级(上)期末试卷(7),共14页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
某校八年级(上)期末数学模拟试卷: 这是一份某校八年级(上)期末数学模拟试卷,共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












