高端精品高中数学二轮专题-椭圆教案

这是一份高端精品高中数学二轮专题-椭圆教案，共7页。
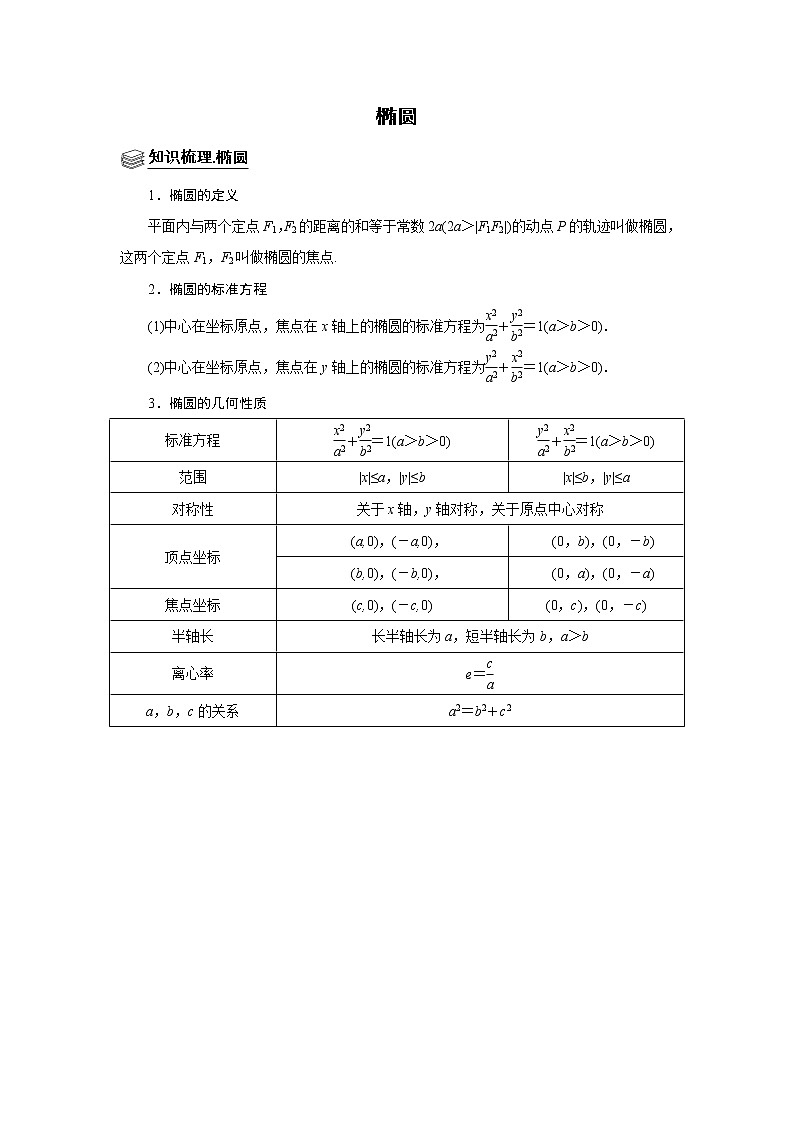
椭圆知识梳理.椭圆1．椭圆的定义平面内与两个定点F1，F2的距离的和等于常数2a(2a＞|F1F2|)的动点P的轨迹叫做椭圆，这两个定点F1，F2叫做椭圆的焦点. 2．椭圆的标准方程(1)中心在坐标原点，焦点在x轴上的椭圆的标准方程为＋＝1(a＞b＞0)．(2)中心在坐标原点，焦点在y轴上的椭圆的标准方程为＋＝1(a＞b＞0)．3．椭圆的几何性质标准方程＋＝1(a＞b＞0)＋＝1(a＞b＞0)范围|x|≤a，|y|≤b|x|≤b，|y|≤a对称性关于x轴，y轴对称，关于原点中心对称顶点坐标　(a,0)，(－a,0)，　(0，b)，(0，－b)　(b,0)，(－b,0)，　(0，a)，(0，－a)焦点坐标(c,0)，(－c,0)(0，c)，(0，－c)半轴长长半轴长为a，短半轴长为b，a＞b离心率e＝a，b，c的关系a2＝b2＋c2       题型一. 椭圆及其性质1．如图，已知椭圆C的中心为原点O，为椭圆C的左焦点，P为椭圆C上一点，满足|OP|＝|OF|且|PF|＝4，则椭圆C的标准方程为　                　．2．平面直角坐标系中，椭圆C中心在原点，焦点F1、F2在x轴上，离心率为．过点F1的直线l与C交于A、B两点，且△ABF2周长为，那么C的方程为（　　）A． B． C． D．3．设F1，F2为椭圆C：1的两个焦点，M为C上一点且在第一象限．若△MF1F2为等腰三角形，则M的坐标为　                　．4．已知椭圆C的焦点为F1（﹣1，0），F2（1，0）．过F2的直线与C交于A，B两点．若2|AF2|＝3|BF2|，|BF1|＝2|BF2|，则C的方程为（　　）A． B． C． D．5．已知点A（1，1）而且F1是椭圆1的左焦点，P是椭圆上任意一点，求|PF1|+|PA|的最大值和最小值．
题型二. 焦点三角形1．过椭圆1（a＞b＞0）的中心做一直线交椭圆于P，Q两点，F是椭圆的一个焦点，则△PFQ的周长的最小值为　      　．2．已知F1，F2是椭圆的焦点，P在椭圆上，且，则点P到x轴的距离为　                　．3．已知F是椭圆1（a＞b＞0）的一个焦点，若直线y＝kx与椭圆相交于A，B两点，且∠AFB＝120°，则椭圆离心率的取值范围是（　　）A． B． C． D．4．已知椭圆的左、右焦点分别为F1，F2，过F2的直线与椭圆C交于M，N两点．设线段NF1的中点为D，若，且，则椭圆C的离心率为（　　）A． B． C． D．5．椭圆C：的左、右焦点分别是F1，F2离心率为，过F1且垂直于x轴的直线被椭圆C截得的线段长为1．（1）求椭圆C的方程；（2）点P是椭圆C上除长轴端点外的任一点，连接PF1，PF2，设∠F1PF2的角平分线PM交C的长轴于点M（m，0），求m的取值范围； 
题型三. 椭圆第二定义——焦半径公式1．过椭圆左焦点F，倾斜角为60°的直线交椭圆于A、B两点，若|FA|＝2|FB|，则椭圆的离心率为（　　）A． B． C． D．2．椭圆两个焦点分别是F1，F2，点P是椭圆上任意一点，则的取值范围是（　　）A．[1，4] B．[1，3] C．[﹣2，1] D．[﹣1，1]3．已知椭圆（a＞b＞0）的短轴长为2，上顶点为A，左顶点为B，F1，F2分别是椭圆的左、右焦点，且△F1AB的面积为，点P为椭圆上的任意一点，则的取值范围为（　　）A．[1，2] B．[] C．[] D．[1，4] 题型四. 离心率之焦点三角形1．设椭圆C：1（a＞b＞0）的左、右焦点分别为F1，F2，P是C上的点，PF2⊥F1F2，∠PF1F2＝30°，则C的离心率为　                　．2．已知椭圆C：（a＞b＞0）的左、右焦点分别为F1，F2，M为椭圆上一点，，线段MF2的延长线交椭圆C于点N，若|MF1|，|MN|，|NF1|成等差数列，则椭圆C的离心率为（　　）A． B． C． D．3．已知椭圆的左焦点为F，C与过原点的直线相交于A，B两点，连接AF、BF，若|AB|＝10，|AF|＝6，cos∠ABF，则C的离心率e＝　              　．
题型五. 离心率之寻求等量关系1．设F1、F2是椭圆E：1（a＞b＞0）的左、右焦点，P为直线x上一点，△F2PF1是底角为30°的等腰三角形，则E的离心率为（　　）A． B． C． D．2．椭圆1（a＞b＞0）的右焦点F（c，0）关于直线yx的对称点Q在椭圆上，则椭圆的离心率是　                　．3．已知O为坐标原点，F是椭圆C：1（a＞b＞0）的左焦点，A，B分别为C的左，右顶点．P为C上一点，且PF⊥x轴，过点A的直线l与线段PF交于点M，与y轴交于点E．若直线BM经过OE的中点，则C的离心率为（　　）A． B． C． D． 题型六.离心率取值范围之椭圆的有界性1．椭圆1（a＞b＞0）的两个焦点为F1，F2，若P为椭圆上一点，且|PF1|＝3|PF2|，则该椭圆离心率的取值范围为（　　）A．（0，] B．[，1） C．（0，] D．[，1）2．椭圆1（a＞b＞0）的二个焦点F1（﹣c，0），F2（c，0），M是椭圆上一点，且•0，则离心率e的取值范围　                　．3．已知F1（﹣c，0），F2（c，0）为椭圆1（a＞b＞0）的两个焦点，P为椭圆上一点且•c2，则此椭圆离心率的取值范围是　                　．4．已知椭圆1（a＞b＞0）的左、右焦点分别为F1（﹣c，0），F2（c，0），若椭圆上存在一点P使，则该椭圆的离心率的取值范围为　                　．
题型七.椭圆的第三定义——点差法1．椭圆C：的左、右顶点分别为A1、A2，点P在C上且直线PA2斜率的取值范围是[﹣2，﹣1]，那么直线PA1斜率的取值范围是（　　）A． B． C． D．2．已知椭圆C：的长轴长为4，若点P是椭圆C上任意一点，过原点的直线l与椭圆相交于M、N两点，记直线PM、PN的斜率分别为KPM、KPN，当时，则椭圆方程为（　　）A． B． C． D．3．已知椭圆C：9x2+y2＝m2（m＞0），直线l不过原点O且不平行于坐标轴，l与C有两个交点A，B，线段AB的中点为M．（1）证明：直线OM的斜率与l的斜率的乘积为定值；    课后作业. 椭圆1．已知点A（0，1），而且F1是椭圆1的左焦点，点P是该椭圆上任意一点，则|PF1|+|PA|的最小值为（　　）A．6 B．6 C．6 D．62．以椭圆的右焦点F2为圆心作一个圆，使此圆过椭圆中心并交椭圆于M，N两点，若过椭圆左焦点F1的直线MF1是圆F2的切线，则该椭圆的离心率为　             　．3．已知点P（﹣2，）在椭圆C：1（a＞b＞0）上，过点P作圆O：x2+y2＝2的切线，切点为A，B，若直线AB恰好过椭圆C的左焦点F，则a2+b2的值是（　　）A．13 B．14 C．15 D．164．如图，从椭圆上一点P向x轴作垂线，垂足恰为左焦点F1，又点A是椭圆与x 轴正半轴的交点，点B是椭圆与y轴正半轴的交点，且AB∥OP，则椭圆的离心率为（　　）A． B． C． D．5．若点O和点F分别为椭圆的中心和左焦点，点P为椭圆上任意一点，则的最小值为（　　）A． B．3 C．8 D．156．如图，在平面直角坐标系xOy中，A1，A2，B1，B2为椭圆1（a＞b＞0）的四个顶点，F为其右焦点，直线A1B2与直线B1F相交于点T，线段OT与椭圆的交点为M，且则该椭圆的离心率为　                　．