

所属成套资源:高中数学二轮专题教案
- 高端精品高中数学二轮专题-单调性(带答案)教案 教案 6 次下载
- 高端精品高中数学二轮专题-奇偶性教案 教案 6 次下载
- 高端精品高中数学二轮专题-对称性与周期性教案 教案 6 次下载
- 高端精品高中数学二轮专题-对称性与周期性(带答案)教案 教案 6 次下载
- 高端精品高中数学二轮专题-函数图像教案 教案 5 次下载
高端精品高中数学二轮专题-奇偶性(带答案)教案
展开
这是一份高端精品高中数学二轮专题-奇偶性(带答案)教案,共8页。
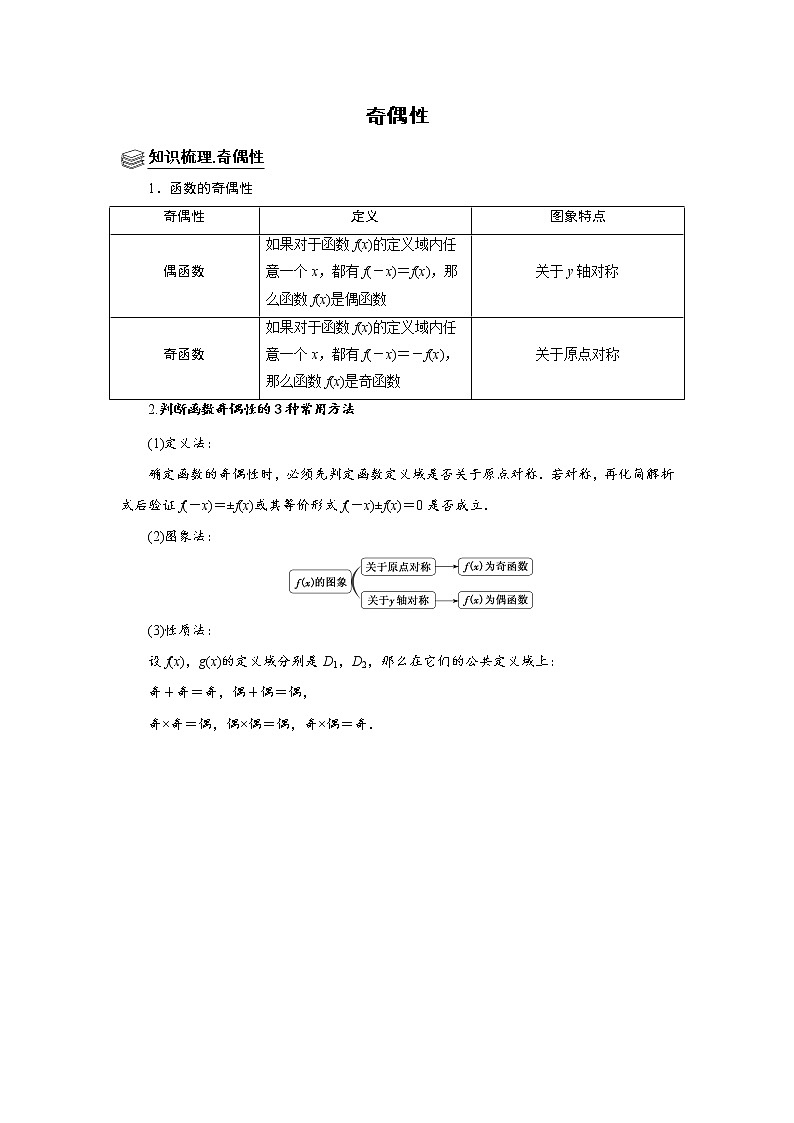
奇偶性知识梳理.奇偶性1.函数的奇偶性奇偶性定义图象特点偶函数如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x),那么函数f(x)是偶函数关于y轴对称奇函数如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)是奇函数关于原点对称2.判断函数奇偶性的3种常用方法(1)定义法:确定函数的奇偶性时,必须先判定函数定义域是否关于原点对称.若对称,再化简解析式后验证f(-x)=±f(x)或其等价形式f(-x)±f(x)=0是否成立.(2)图象法:(3)性质法:设f(x),g(x)的定义域分别是D1,D2,那么在它们的公共定义域上:奇+奇=奇,偶+偶=偶,奇×奇=偶,偶×偶=偶,奇×偶=奇. 题型一. 判断奇偶性1.已知函数f,则下列结论正确的是( )A.f(x)g(x)为奇函数 B.f(x)g(x)为偶函数 C.f(x)+g(x)为奇函数 D.f(x)+g(x)为非奇非偶函数【解答】解:f(x)的定义域为2x﹣1≠0,x≠0,,故函数f(x)为奇函数,g(x)定义域为R且g(﹣x)=﹣g(x),函数g(x)也为奇函数,∴f(x)g(x)为偶函数,f(x)+g(x)为奇函数,故选:BC.2.下列函数中,在定义域内单调递增且是奇函数的是( )A. B.y=sinx C.y=2x﹣2﹣x D.y=|x﹣1|【解答】解:因为f(﹣x)+f(x)=log2()+log2()=log2(x2+1﹣x2)=0,所以f(﹣x)=﹣f(x),即f(x)为奇函数,但是f(1)=log2(),f(0)=0,f(1)<f(0),不满足单调递增,不符合题意;y=sinx在R上不单调,不符合题意;y=2x﹣2﹣x在R上单调递增,且f(﹣x)=2﹣x﹣2x=﹣f(x),即f(x)为奇函数,符合题意;y=|x﹣1|为非奇非偶函数,不符合题意;故选:C.3.设函数f(x)=x(ex+e-x),则对f(x)的奇偶性和在(0,+∞)上的单调性判断的结果是( )A.奇函数,单调递增 B.偶函数,单调递增 C.奇函数,单调递减 D.偶函数,单调递减【解答】解:根据题意,函数f(x)=x(ex+e﹣x),其定义域为R,有f(﹣x)=(x)(e﹣x+ex)=﹣x(ex+e﹣x)=﹣f(x),则f(x)为奇函数,又由f′(x)=(ex+e﹣x)+x(ex﹣e﹣x),区间(0,+∞)上,ex>1>e﹣x>0,则有f′(x)>0,则f(x)在区间(0,+∞)上是增函数,故选:A. 题型二. 已知奇偶性求参、求值1.若函数f(x)(k为常数)在定义域上为奇函数,则k的值为 ±1 .【解答】解:∵函数f(x)∴f(﹣x)=﹣f(x)∴∴(k2﹣1)(2x)2=1﹣k2∴(k2﹣1)=0∴k=±1验证k=±1时,满足函数f(x)在定义域上为奇函数,故答案为:±1.2.若函数f(x)=xln(x)为偶函数,则a的值为( )A.0 B.1 C.﹣1 D.1或﹣1【解答】解:∵函数f(x)=xln(x)为偶函数,x∈R,∴设g(x)=ln(x)是奇函数,则g(0)=0,即ln0,则1,则a=1.故选:B.3.已知f(x)是奇函数,且当x<0时,f(x)=﹣eax.若f(ln2)=8,则a= .【解答】解:∵f(x)是奇函数,∴f(﹣ln2)=﹣8,又∵当x<0时,f(x)=﹣eax,∴f(﹣ln2)=﹣e﹣aln2=﹣8,∴﹣aln2=ln8,∴a=﹣3.故答案为:﹣3 题型三.两个重要结论1.已知函数f(x),f(a)=4,则f(﹣a)= ﹣2 .【解答】解:根据题意,f(x),则f(﹣x),则f(x)+f(﹣x)=2,即有f(a)+f(﹣a)=2,又由f(a)=4,则f(﹣a)=﹣2;故答案为:﹣22.已知函数f(x)=(x2﹣2x)sin(x﹣1)+x+1在[﹣1,3]上的最大值为M,最小值为m,则M+m= 4 .【解答】解:∵f(x)=(x2﹣2x)sin(x﹣1)+x+1=[(x﹣1)2﹣1]sin(x﹣1)+x﹣1+2令g(x)=(x﹣1)2sin(x﹣1)﹣sin(x﹣1)+(x﹣1),而g(2﹣x)=(x﹣1)2sin(1﹣x)﹣sin(1﹣x)+(1﹣x),∴g(2﹣x)+g(x)=0,则g(x)关于(1,0)中心对称,则f(x)在[﹣1,3]上关于(1,2)中心对称.∴M+m=4.故答案为:4. 题型四. 奇偶性和单调性综合1.设函数f(x)=ln|2x+1|﹣ln|2x﹣1|,则f(x)( )A.是偶函数,且在 单调递增 B.是奇函数,且在 单调递增 C.是偶函数,且在单调递增 D.是奇函数,且在 单调递增【解答】解:由,得x≠±.又f(﹣x)=ln|﹣2x+1|﹣ln|﹣2x﹣1|=﹣(ln|2x+1|﹣ln|2x﹣1|)=﹣f(x),∴f(x)为奇函数,由f(x)=ln|2x+1|﹣ln|2x﹣1|=ln||,∵11.可得内层函数t=||的图象如图,在(﹣∞,),((,+∞)上单调递减,在(,)上单调递增,又对数式y=lnt是定义域内的增函数,由复合函数的单调性可得,f(x)在(,)上单调递增,在(﹣∞,),((,+∞)上单调递减.故选:B.2.已知函数f(x)是定义在R上的偶函数,且在[0,+∞)上单调递增,则三个数a=f(﹣log313),b=f(2cos),c=f(20.6)的大小关系为( )A.a>b>c B.a>c>b C.b>a>c D.c>a>b【解答】解:根据题意,2=log39<log313<log327=3,,1<20.6<21=2,则有,函数f(x)是定义在R上的偶函数,则a=f(﹣log313)=f(log313),又由f(x)在[0,+∞)上单调递增,则,即a>c>b,故选:B.3.函数f(x)在(﹣∞,+∞)单调递减,且为奇函数.若f(1)=﹣1,则满足﹣1≤f(x﹣2)≤1的x的取值范围是( )A.[﹣2,2] B.[﹣1,1] C.[0,4] D.[1,3]【解答】解:∵函数f(x)为奇函数.若f(1)=﹣1,则f(﹣1)=1,又∵函数f(x)在(﹣∞,+∞)单调递减,﹣1≤f(x﹣2)≤1,∴f(1)≤f(x﹣2)≤f(﹣1),∴﹣1≤x﹣2≤1,解得:x∈[1,3],故选:D.4.若定义在R的奇函数f(x)在(﹣∞,0)单调递减,且f(2)=0,则满足xf(x﹣1)≥0的x的取值范围是( )A.[﹣1,1]∪[3,+∞) B.[﹣3,﹣1]∪[0,1] C.[﹣1,0]∪[1,+∞) D.[﹣1,0]∪[1,3]【解答】解:∵定义在R的奇函数f(x)在(﹣∞,0)单调递减,且f(2)=0,f(x)的大致图象如图:∴f(x)在(0,+∞)上单调递减,且f(﹣2)=0;故f(﹣1)<0;当x=0时,不等式xf(x﹣1)≥0成立,当x=1时,不等式xf(x﹣1)≥0成立,当x﹣1=2或x﹣1=﹣2时,即x=3或x=﹣1时,不等式xf(x﹣1)≥0成立,当x>0时,不等式xf(x﹣1)≥0等价为f(x﹣1)≥0,此时,此时1<x≤3,当x<0时,不等式xf(x﹣1)≥0等价为f(x﹣1)≤0,即,得﹣1≤x<0,综上﹣1≤x≤0或1≤x≤3,即实数x的取值范围是[﹣1,0]∪[1,3],故选:D.5.已知定义域为R的函数f(x)是奇函数.若对任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0恒成立,则k的取值范围为 k .【解答】解:∵f(x)是R上的奇函数,∴f(0)=0⇒b=1;从而有f(x),又由f(﹣1)=﹣f(1)⇒a=2;∴f(x),由上式可知f(x)在R上为减函数,又∵f(x)为奇函数,f(t2﹣2t)+f(2t2﹣k)<0⇔f(t2﹣2t)<f(k﹣2t2),∵f(x)是R上的减函数,由上式可得t2﹣2t>k﹣2t2,即对一切t∈R有3t2﹣2t﹣k>0,从而△=4+12k<0,解得k.6.设f(x)是定义在R上的奇函数,且当x≥0时,f(x)=x2,若对任意的x∈[t,t+2],不等式f(x+t)≥2f(x)恒成立,则实数t的取值范围是( )A. B.[2,+∞) C.(0,2] D.【解答】解:(排除法)当则得,即在时恒成立,而最大值,是当时出现,故的最大值为0,则f(x+t)≥2f(x)恒成立,排除B项,同理再验证t=3时,f(x+t)≥2f(x)恒成立,排除C项,t=﹣1时,f(x+t)≥2f(x)不成立,故排除D项故选:A.7.已知函数f(x)=x3﹣2x+ex,其中e是自然对数的底数.若f(a﹣1)+f(2a2)≤0.则实数a的取值范围是 [﹣1,] .【解答】解:函数f(x)=x3﹣2x+ex的导数为:f′(x)=3x2﹣2+ex2+20,可得f(x)在R上递增;又f(﹣x)+f(x)=(﹣x)3+2x+e﹣x﹣ex+x3﹣2x+ex0,可得f(x)为奇函数,则f(a﹣1)+f(2a2)≤0,即有f(2a2)≤﹣f(a﹣1)由f(﹣(a﹣1))=﹣f(a﹣1),f(2a2)≤f(1﹣a),即有2a2≤1﹣a,解得﹣1≤a,故答案为:[﹣1,].8.设函数f(x)=ln(1+|x|),则使得f(x)>f(2x﹣1)成立的x的取值范围是( )A.(﹣∞,)∪(1,+∞) B.(,1) C.() D.(﹣∞,)【解答】解:∵函数f(x)=ln(1+|x|)为偶函数,且在x≥0时,f(x)=ln(1+x),导数为f′(x)0,即有函数f(x)在[0,+∞)单调递增,∴f(x)>f(2x﹣1)等价为f(|x|)>f(|2x﹣1|),即|x|>|2x﹣1|,平方得3x2﹣4x+1<0,解得:x<1,所求x的取值范围是(,1).故选:B.
相关教案
这是一份高端精品高中数学二轮专题-数列求和(带答案)教案,共17页。
这是一份高端精品高中数学二轮专题-椭圆(带答案)教案,共20页。
这是一份高端精品高中数学二轮专题-奇偶性教案,共3页。









