2020-2021学年7.2 探索平行线的性质优秀综合训练题

2022年苏科版数学七年级下册

7.2《探索平行线的性质》课时练习

一、选择题

1.如图，直线AB∥CD，则下列结论正确的是（　　）

A.∠1=∠2       B.∠3=∠4      C.∠1+∠3=180°     D.∠3+∠4=180°

2.如图，已知两直线l1与l2被第三条直线l3所截，下列等式一定成立的是(　　)

A．∠l=∠2    B．∠2=∠3     C．∠2+∠4=180°  D．∠1+∠4=180°

3.如图，已知AB∥CD，BC平分∠ABE，∠C=33°，则∠BED的度数是（　  　）

  A.16°                       B.33°                        C.49°                      D.66°

4.已知直线a∥b，∠1和∠2互余，∠3=121°，那么∠4等于（      ）

  A．159°                      B．149°                          C．139°                    D．21°

5.如图,直线AB∥CD,∠A=40°,∠D=45°,则∠1的度数是（  ）

A.80°       B.85°        C.90°        D.95°

6.下面四个图形中，∠1=∠2一定成立的是（    ）

7.如图,AB∥CD∥EF,BC∥AD,AC平分∠BAD,则图中与∠AGE相等的角（    ）

A.2个                         B.3个                        C.4个                         D.5个

8.如图，AB//CD，用含∠1、∠2、∠3的式子表示∠4，则∠4的值为（       ）

A.∠1+∠2-∠3             B.∠1+∠3-∠2  

C.180°+∠3-∠1-∠1       D.∠2+∠3-∠1-180°

二、填空题

9.如图，已知∠1=∠2=∠3=59°，则∠4=　　　　. 

10.如图,已知AD∥BE,∠1=20°,∠DCE=45°,则∠2的度数为      ．

11.如图,已知AF∥EC,AB∥CD,∠A=65°,则∠C=     度．

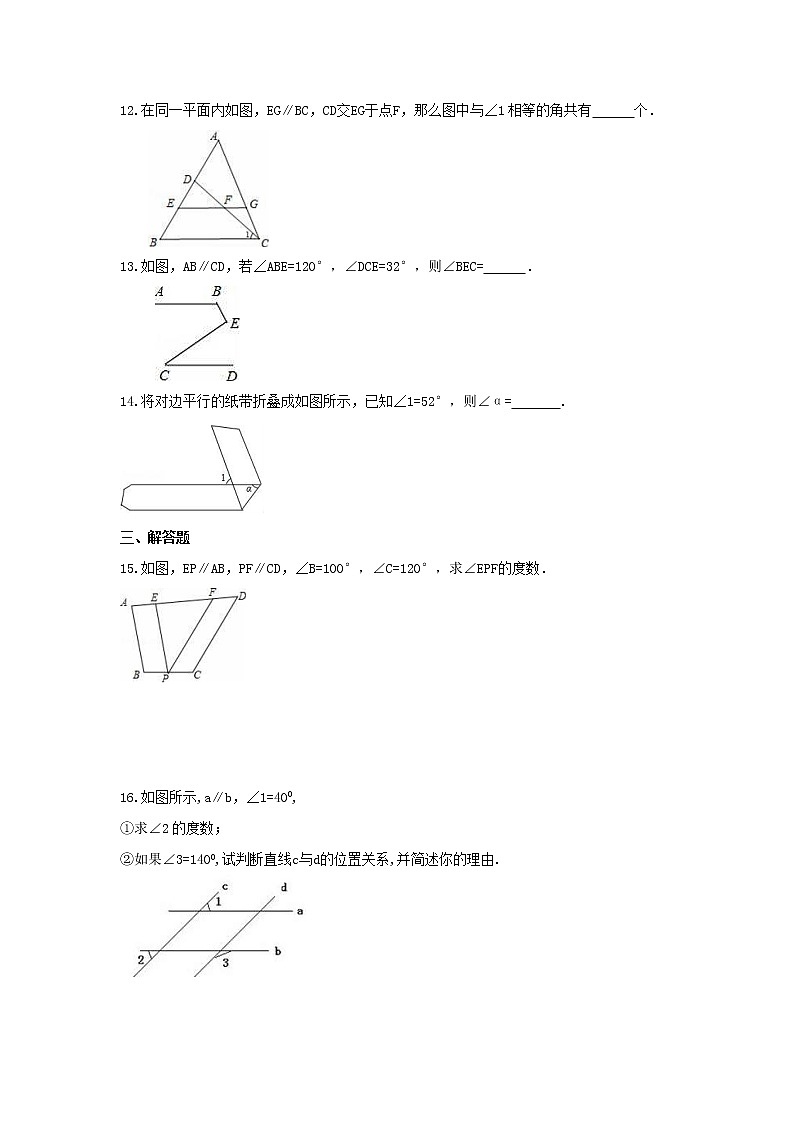
12.在同一平面内如图，EG∥BC，CD交EG于点F，那么图中与∠1相等的角共有      个．

13.如图，AB∥CD，若∠ABE=120°，∠DCE=32°，则∠BEC=      ．

14.将对边平行的纸带折叠成如图所示，已知∠1=52°，则∠α=　   　.

三、解答题

15.如图，EP∥AB，PF∥CD，∠B=100°，∠C=120°，求∠EPF的度数．

16.如图所示,a∥b，∠1=400,

①求∠2的度数；

②如果∠3=1400,试判断直线c与d的位置关系,并简述你的理由.

17.如图,已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数．

18.如图,直线AB∥CD，直线AB、CD被直线EF所截，EG平分∠BEF，FG平分∠DFE，

（1）若∠AEF=50°，求∠EFG的度数．

（2）判断EG与FG的位置关系，并说明理由．

参考答案

1.D.

2.D.

3.D．

4.B

5.B

6.B.

7.D

8.D

9.答案为：121°

10.答案为：25°．

11.答案为：65

12.答案为：2．

13.答案为：92°．

14.答案为：64°.

15.解：∵EP∥AB，

∴∠BPE=180°﹣∠B=180°﹣100°=80°，

∵PF∥CD，

∴∠CPF=180°﹣∠C=180°﹣120°=60°，

∴∠EPF=180°﹣∠BPE﹣∠CPF=180°﹣80°﹣60°=40°．

16.解：①∵a∥b ∠1=400 (已知)

∴∠4=∠1=400 (两直线平行，同位角相等。

∴∠2=∠4=400(对顶角相等)

②∵∠2=400 (已证)

又∵∠5＋∠2=1800(互补的意义)

∴∠5=1400 (等式的性质)

又∵∠3=1400(已知)

∴∠3=∠5(等量代换)

∴c∥d(同位角相等，两直线平行。)

17.解：∵AB∥CF，∠ABC=70°，

∴∠BCF=∠ABC=70°，

又∵DE∥CF，∠CDE=130°，

∴∠DCF+∠CDE=180°，

∴∠DCF=50°，

∴∠BCD=∠BCF﹣∠DCF=70°﹣50°=20°．

18.解：