初中数学沪科版七年级上册1.4 有理数的加减教课内容课件ppt

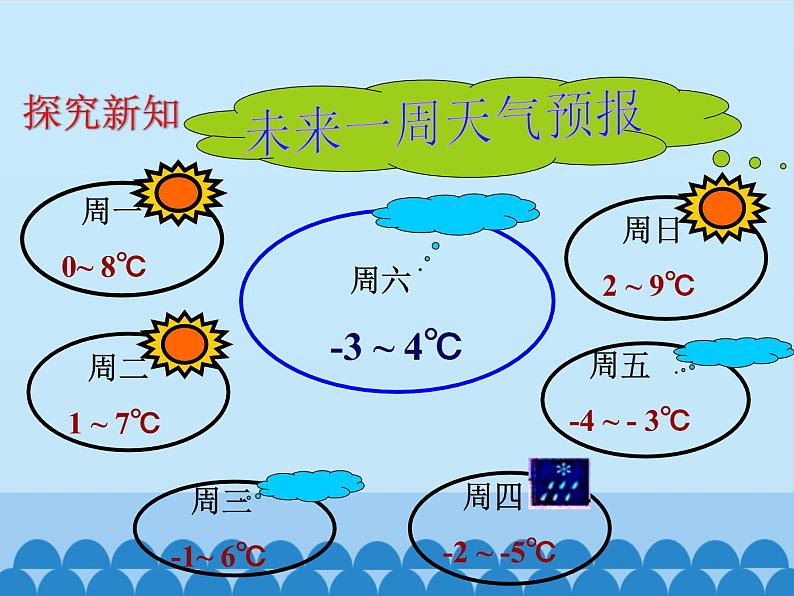
这是一份初中数学沪科版七年级上册1.4 有理数的加减教课内容课件ppt，共18页。PPT课件主要包含了有理式加法法则，温习旧知，探究新知，--3，++37，0++3，-1++3，-5++3，++3，有理数减法法则等内容，欢迎下载使用。
1、同号两数相加，取相同的符号，并把绝对值相加。
2、异号两数相加，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值。互为相反数的两数相加等于0。
3、一个数同0相加，仍得这个数。
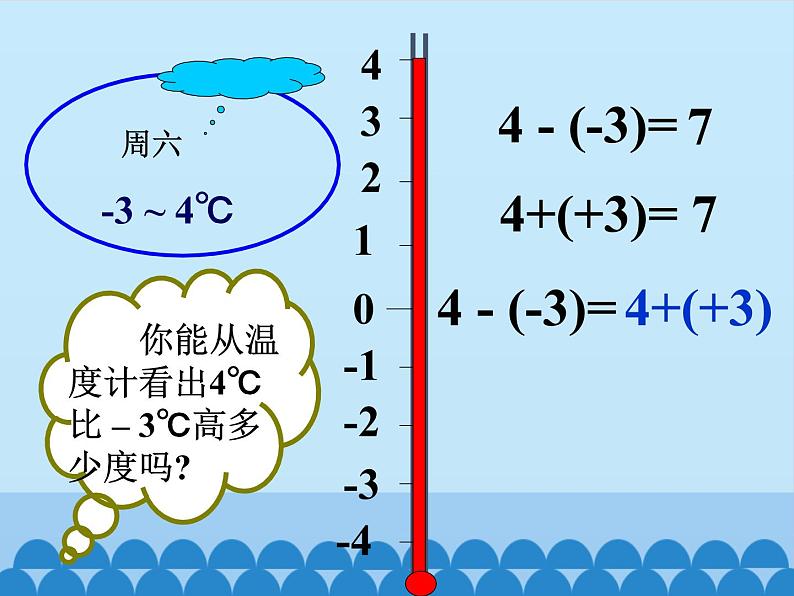
把4换成其他数字，用上面的方法试试看.
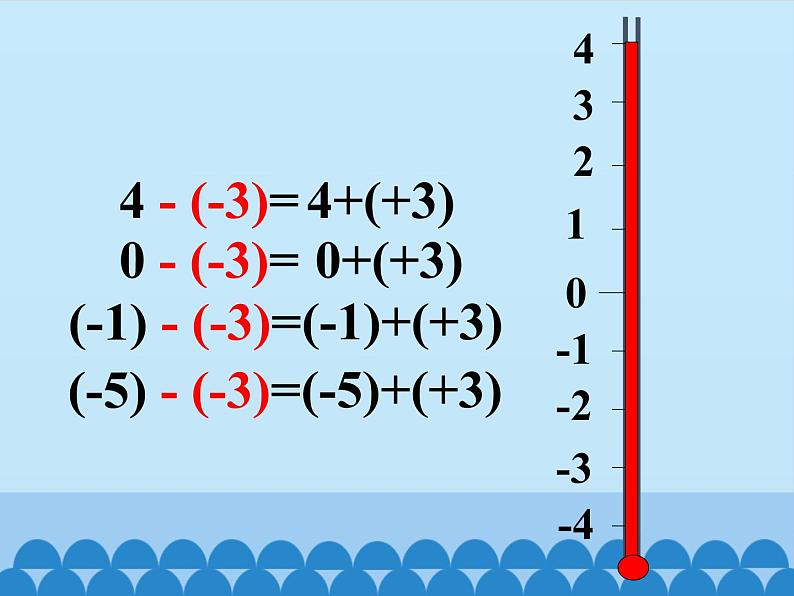
(-1) - (-3)=
(-5) - (-3)=
这些数减(– 3)的结果与它们____(+3)的结果是相同的.
　　观察上面四对算式，对有理数的减法运算你能得出什么结论？
减去一个数,等于加上这个数的相反数.
a – b = a + (-b)
解： （1） （-16）-（-9） =（-16）+（+9）=-7 （2） 2-7=2+（-7）=-5 （3） 0-（-2.5）=0+(+2.5)=2.5 （4）（-2.8）-（+1.7） =(-2.8)+(-1.7)=-4.5
解：20-(-10)=20+10=30(分） 即答对一题与答错一题相差30分
2、判断（1）在有理数的加法中，两数的和一定比加数大（ ）（2）两个数相减，被减数一定比减数大（ ）（3）两数之差一定小于被减数（ ）（4）0减去任何数，差都为负数（ ）（5）较大的数减去较小的数，差一定是正数（ ）
3、填空（1）（-7） -（ - 14）= . （2）0 - = 4.（3）一个加数是1.8，和是－0.81，则另一个加数为 .（4）- 的绝对值的相反数与 的相反数的差 .（5） 比7的相反数小5.（6）∣a∣= 8， ∣b∣= 3，且a < b，则a-b = .
　 高斯(1777~1855) 德国数学家，他的祖父是农民，父亲是泥匠，家境贫寒。但高斯在早年就表现出非凡的数学天才：年仅三岁，就学会了算术；八岁时就以著名的1加到100，而深得老师和同学的钦佩；十九岁时就给出了可用尺规作图的正多边形的条件，从而解决了两千多年来悬而未决的难题。高斯的数学成就遍及各个领域，在数学许多分支的贡献都有着划时代的意义，被誉为历史上最伟大的数学家之一。
1+2+3+…+99+100
计算： -1-2-3-…-99-100
解： -1-2-3-…-99-100 =（-1）+（-2）+（-3）+…+（-99）+（-100）
=（1+100）+（2+99）+…+（50+51）
补充：数轴上的点A、B、C、D、E分别是-4，-1.5，-0.5，1.5，3，回答下列问题：
(1)A与B两点间的距离是多少?(2)C与D两点间的距离是多少?(3)D与E两点间的距离是多少?(4)你能发现所得结果与相应两数的差有什么关系吗?
可以发现:数轴上任意两点间的距离是相应两数差的绝对值.
全班学生分为五个组进行游戏，每组的基本分为100分，答对一题加50分，答错一题扣50分。游戏结束时，各组的分数如下：第一组 第二组 第三组 第四组 第五组 100 150 -400 350 -100（1）第一名超出第二名多少分？（2）第二名超出第五名多少分？
1. 减去一个数，等于加上这个数的相反数;
2. 0减去一个数，就得到这个数的相反数;
3. 减法运算转化成加法的过程中，必须同时改变减号和减数的符号.
有理数的减法法则是一个转化法则，减号转化为加号，同时要注意减数变为它的相反数，这样就可以用加法来解决减法问题. 在课堂上，出现了小数减大数的情形，这就说明不仅仅是大的数才能减去小的数，在有理数范围里，任何两个数都可以相减.