初中第9章 多边形9.2 多边形的内角和与外角和教学课件ppt

这是一份初中第9章 多边形9.2 多边形的内角和与外角和教学课件ppt，共18页。PPT课件主要包含了学习目标，掌握多边形外角和，问题1，知识精讲，问题2，n边形外角和，360°，n×180°，与边数无关，典例解析等内容，欢迎下载使用。
理解多边形外角的定义.
灵活运用多边形内角和与外角和公式解决有关问题.
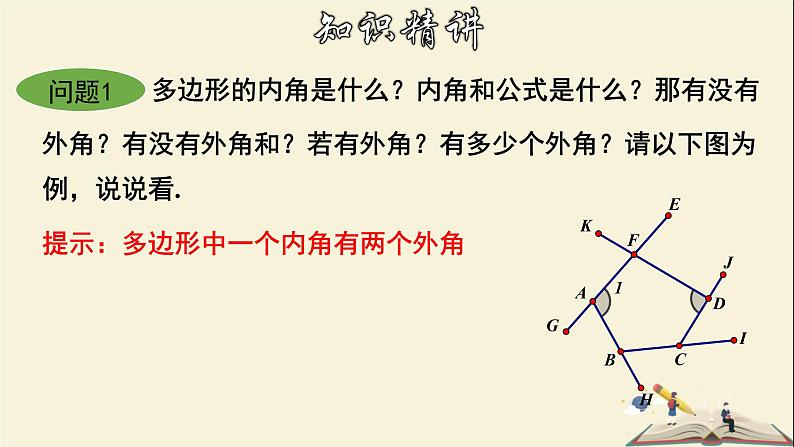
多边形的内角是什么？内角和公式是什么？那有没有外角？有没有外角和？若有外角？有多少个外角？请以下图为例，说说看.
提示：多边形中一个内角有两个外角
1.什么样的角时多边形的外角？2.怎样的角的和才算是多边形的外角和呢？
多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角.
在每个顶点处取这个多边形的一个外角，他们的和叫做这个多边形的外角和.
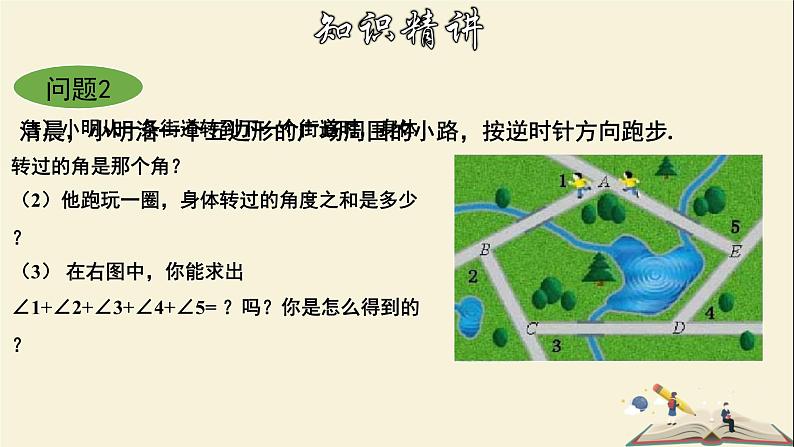
（1）小明从一条街道转到下一个街道时，身体转过的角是那个角？（2）他跑玩一圈，身体转过的角度之和是多少？（3） 在右图中，你能求出∠1+∠2+∠3+∠4+∠5= ？吗？你是怎么得到的？
清晨，小明沿一个五边形的广场周围的小路，按逆时针方向跑步.
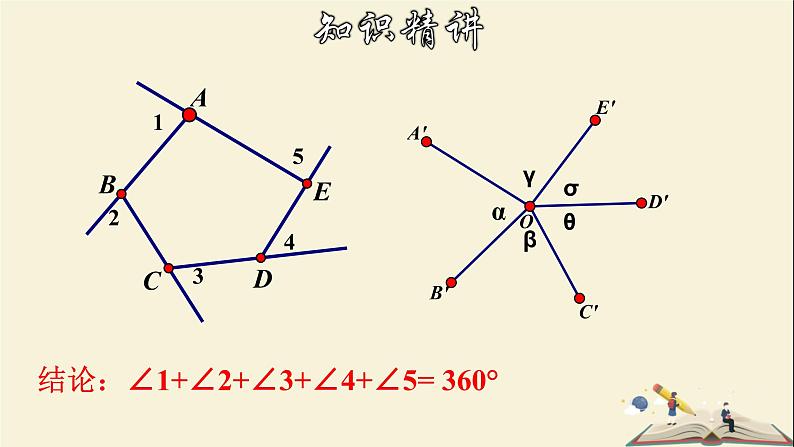
结论：∠1+∠2+∠3+∠4+∠5= 360°
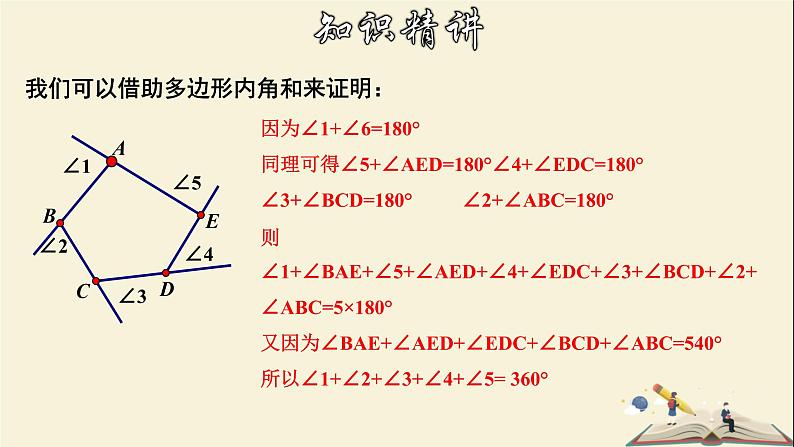
我们可以借助多边形内角和来证明：
因为∠1+∠6=180°同理可得∠5+∠AED=180°∠4+∠EDC=180°∠3+∠BCD=180° ∠2+∠ABC=180°则∠1+∠BAE+∠5+∠AED+∠4+∠EDC+∠3+∠BCD+∠2+∠ABC=5×180°又因为∠BAE+∠AED+∠EDC+∠BCD+∠ABC=540°所以∠1+∠2+∠3+∠4+∠5= 360°
那如果广场的形状是六边形、七边形、八边形…n边形呢？结论还是一样的么？
在n边形的每个顶点处各取一个外角，这些外角的和叫做n边形的外角和．
n边形的外角和等于360°.
－(n－2) × 180°
=n个平角-n边形内角和
例：一个多边形的每个外角都是72°，这个多边形是几边形？
解：设多边形的边数为n,根据题意， 得 n•72°=360° 解得 n=5因此这个多边形是五边形
解：设多边形的边数为n.根据题意， 得 （n-2）•180°=5×360° 解得 n=12因此，这个多边形是十二边形
例：一个多边形的内角和等于它外角和的5倍，这个多边形是几边形
例：已知一个多边形，它的内角和等于外角和的2倍，求这个多边形的边数.
解： 设多边形的边数为n. ∵它的内角和等于 (n－2)•180°， 多边形外角和等于360°， ∴ (n－2)•180°=2× 360º. 解得 n=6. ∴这个多边形的边数为6.
例：已知一个多边形的每个内角与外角的比都是7:2，求这个多边形的边数.
解法一：设这个多边形的内角为7x °,外角为2x°,根据题意得
即每个内角是140 °，每个外角是40 °.
360° ÷40 °=9.
答：这个多边形是九边形.
解法二：设这个多边形的边数为n ,根据题意得
一个正多边形的一个外角比一个内角大60°，求这个多边形的每个内角的度数及边数．
解：设该正多边形的内角是x°，外角是y°，则得到一个方程组 解得而任何多边形的外角和是360°，则该正多边形的边数为360÷120=3，故这个多边形的每个内角的度数是60°，边数是三条．
例: 如图，在正五边形ABCDE中，连接BE，求∠BED的度数．
解：由题意得AB=AE,所以∠AEB= (180°-∠A)=36°，所以∠BED=∠AED-∠AEB=108°-36°=72°.
1.一个多边形的外角和是内角和的一半，则它是（ ）边形 A 7 B 6 C 5 D 42.一个多边形的内角和与外角和共540°，则它是（ ）边形A 5 B 4 C 3 D 不确定