初中数学华师大版七年级下册2 旋转的特征教学课件ppt

这是一份初中数学华师大版七年级下册2 旋转的特征教学课件ppt，共15页。PPT课件主要包含了学习目标，旋转的概念，旋转的要素，旋转的特征，复习回顾，知识精讲，典例解析，达标检测，P32等内容，欢迎下载使用。

通过具体的实例进一步认识旋转，掌握旋转的特征.
会利用旋转的特征进行相关的证明和计算，以及画出图形经过旋转运动后形成的图形.
旋转不改变图形大小和形状,只改变图形的位置.
旋转中心.旋转方向和旋转角.
在平面内，将一个图形绕着一个定点沿某个方向转动一个角度的运动叫做图形的旋转，简称旋转.
下列现象中属于旋转的有 ( )个.①地下水位逐年下降；②传送带的移动；③方向盘的转动； ④水龙头的转动；⑤钟摆的运动； ⑥荡秋千.A.2 B.3 C.4 D.5
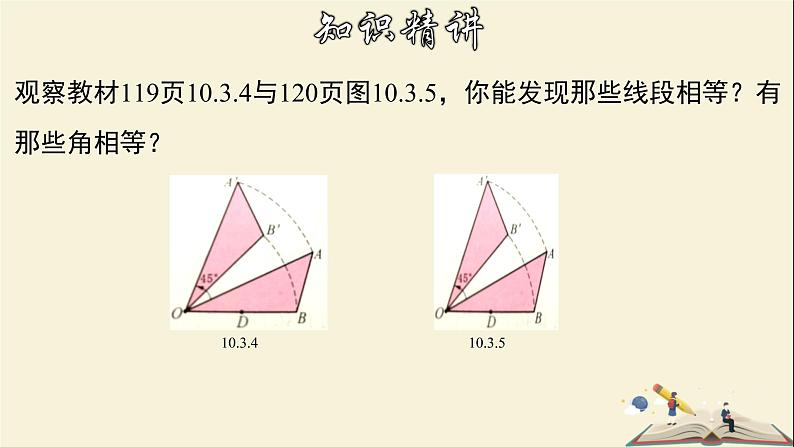
观察教材119页10.3.4与120页图10.3.5，你能发现那些线段相等？有那些角相等？
线段OA、OB都是绕点O逆时针旋转45°到对应线段OA'、OB'所以线段相等的有：角相等的有:
OA=OA' OB=OB' AB=A'B'
∠AOB=∠A'OB' ∠A=∠A' ∠B=∠B'
1.旋转不改变图形的形状和大小；2.旋转前后对应线段相等,对应角相等；3.对应点到旋转中心的距离相等．4.任意一对对应点与旋转中心的连线所成的角都是旋转角．
例1：如图所示， △ABO绕点O旋转得到△CDO，在这个旋转过程中：
(1) 旋转中心是_____;旋转角是_______________;
(2)经过旋转，点A、B分别移到了__________;
(3)若AO=3cm，则CO=__________;
(4) 若∠AOC=55°,∠AOD=25°,则∠BOD=_____ ∠BOC=_______.
∠AOC或∠BOD
例2:画△ABC绕顶点A顺时针旋转45°的图形.
你能说说旋转中有哪些对应元素吗?
画法:⑴以A为顶点, AB为始边顺时针方向画∠BAB =45°，在终边上截取AB’ =AB;⑵同样画边AC , 并连结BC ;则△ABC 就是所求作的旋转图形.则△ABC 就是所求作的旋转图形.
例3:如图，在正方形ABCD中，F为CD边上一点，将△ADF绕A点顺时针旋转90°，到△ABE的位置，
（1）线段AE与AF成怎样的关系？（2）图中的△AEF是什么三角形？
解：(1)相等且互相垂直，证明如下：∵ ADF旋转后能与BAE重合 ∴AF=AE且∠DAF=∠BAE，又∠DAF+∠FAB=90° ∴∠BAE+∠FAB=90°∴∠FAE=90°即AF⊥BE∴AF=BE 且AF⊥BE(2)由（1）可知△AEF是等腰直角三角形
1.一个图形经过平移或旋转，有以下的说法：①对应线段平行；②对应线段相等； ③对应角相等； ④图形的形状和大小都没有发生变化，其中正确的是（ ）A、①②③ B、①②④ C、①③④ D、②③④2.时钟的时针经过1小时，旋转的角度为（ ）A 15° B 30° C 60° D 360°
3.如图，将ΔABC绕点C顺时针方向旋转40°得到ΔA'B'C',若AC⊥A'B'，则∠BAC= .
4.如图，将ΔABC旋转得到ΔA'B'C',下列说法正确的个数有( )①AC=AB' ②BC=B'C' ③∠BAC=∠B'AC' ④∠CAC'=∠BAB'A 1个 B 2个 C 3个 D 4个
5.如图，正方形ABCD中，E为BC边上的一点，将ΔABE旋转后得到的ΔCBF（1）指出旋转中心及旋转角度；（2）判断AE和CF的数量和位置关系；（3）如果正方形的面积是18cm2,ΔBCF的面积是5cm2，问四边形ABCD的面积是多少？
旋转中心是点B,旋转角度是90°
AE=CF AE⊥CF
S四边形ABCD=18-5=13cm2
6.如图，△ADE可由△CAB旋转而成，点B的对应点是E，点A的对应点是D，在平面直角坐标系中，三点坐标为A（1,0）、B（3,0）、C（1,4）.请找出旋转中心P的位置，并写出P的坐标.