高中数学沪教版高中一年级 第二学期5.2任意角的三角比教案设计

5.2(2)  任意角的三角比

一、教学目标设计

(1) 根据任意角的正弦、余弦、正切、余切 、正割、余割的定义，掌握这些三角比的值在各象限的符号；并能根据角的某种三角比值的符号，反馈出可能存在的象限；

(2) 掌握诱导公式一，会运用它们把求任意角的正弦、余弦、正切值分别转化为求的这三种三角比的值．

二、教学重点及难点

任意角的正弦、余弦、正切在各象限内的符号及诱导公式一．

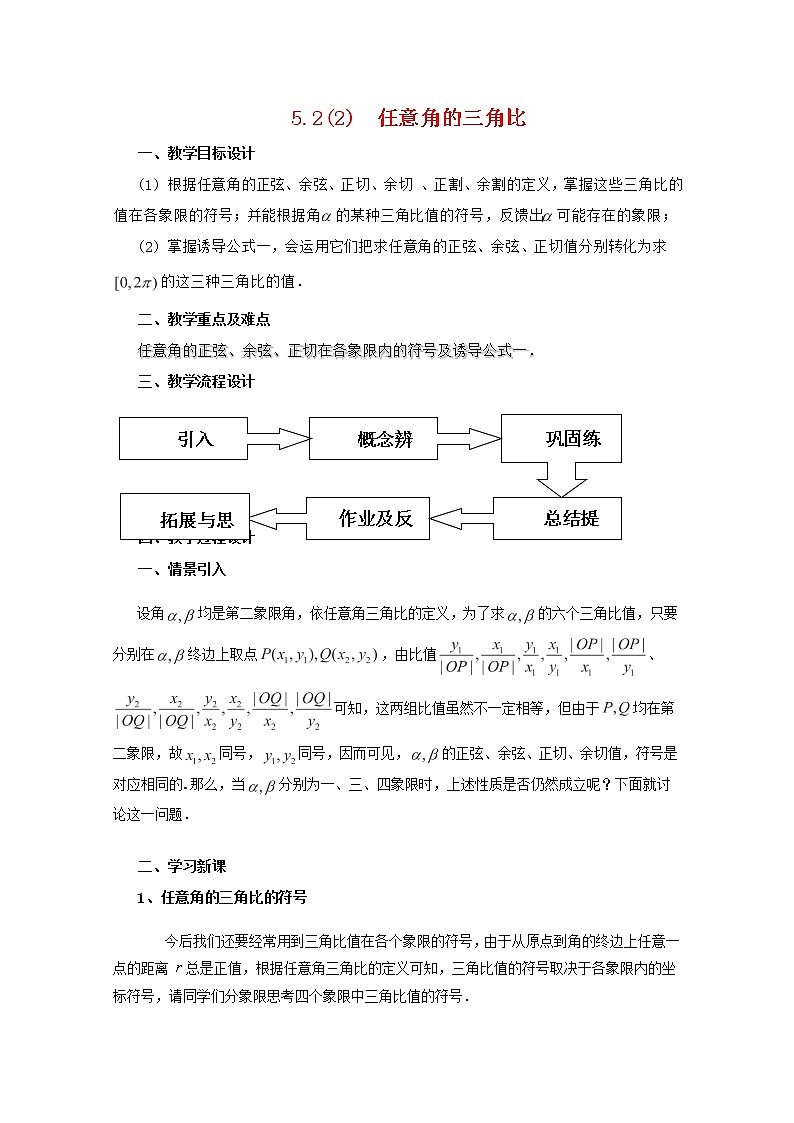
三、教学流程设计

四、教学过程设计          

一、情景引入

设角均是第二象限角，依任意角三角比的定义，为了求的六个三角比值，只要分别在终边上取点，由比值、可知，这两组比值虽然不一定相等，但由于均在第二象限，故同号，同号，因而可见，的正弦、余弦、正切、余切值，符号是对应相同的.那么，当分别为一、三、四象限时，上述性质是否仍然成立呢？下面就讨论这一问题．

二、学习新课

1、任意角的三角比的符号

　　今后我们还要经常用到三角比值在各个象限的符号，由于从原点到角的终边上任意一点的距离 总是正值，根据任意角三角比的定义可知，三角比值的符号取决于各象限内的坐标符号，请同学们分象限思考四个象限中三角比值的符号．

　　观察六个三角比，可发现与，与，与互为倒数，因此它们的符号规律相同．

　　， (1) 当在第一、二象限时，，所以为正；

(2) 当在第三、四象限时，，所以为负．

同理，对于第一、四象限的角是正的，而对于第二、三象限的角是负的．

　　  ，对于第一、三象限的角是正的，而对于第二、四象限的角是负的．

现在我们将以上讨论结果整理成图1．

图1

[说明] 可以表达为正弦和余割上正下负，余弦与正割左负右正，正切与余切一、三象限为正，二、四象限为负．同学们还可以自己用口诀“全正， 正， 正， 正”来记忆．记法多种多样，老师可自由发挥.

2、诱导公式一

　　上节课我们已学过终边重合的角，例如和的终边都与终边位置重合．

　　∵ ，

　　∴由任意角三角比的定义可知它们的三角比值相同，即

　　推广到一般情形，我们可得到诱导公式一：终边重合的角的同一三角比值相等，即

     （）

    （）

     （）

     （）

     （）

     （）

　  [说明]这组公式的作用是把任意角的三角比值问题转化为角的三角比值问题．

3、例题分析

例1．确定下列三角比值符号：

（1） ；（2）；（3）

答：（1）负；（2）负；（3）负.

例2. 求证角为第三象限角的充分必要条件是 ．

证明：必要性：当为第三象限角时，；

充分性：∵成立，∴角的终边可能位于第三或第四象限，也可以位于轴的非正半轴上；又∵成立，∴角的终边可能位于第一或第三象限，因为要同时成立，所以角的终边只可能位于第三象限，于是角为第三象限角．

例3. 求下列三角比值：

（1）；（2）；（3）．

答：（1）； （2）；（3）.

例4. 如果在第二象限，那么的值是什么符号？

答：∵在第二象限，∴，

　　∴，∴ .

例5. 若是第二象限的角，且，问是第几象限角？

答：是第三象限的角．

例6. 求值：

答：原式＝0.

三、巩固练习

练习5.2（2）

四、课堂小结

(1) 任意角的三角比的值在各象限的符号；

(2) 诱导公式一.

五、课后作业

练习册  P15-17

习题5.2  A组   3，4，5，6，7， 8

习题5.2  B组   2，3