






沪教版高中一年级 第一学期3.1函数的概念教学课件ppt
展开1.初中所学的函数的概念是什么?
在一个变化过程中有两个变量x和y,如果对于x的每一个值,y都有唯一的值与它对应. 那么就说y是x的函数,其中x叫做自变量.
2、请同学们考虑以下几个问题:
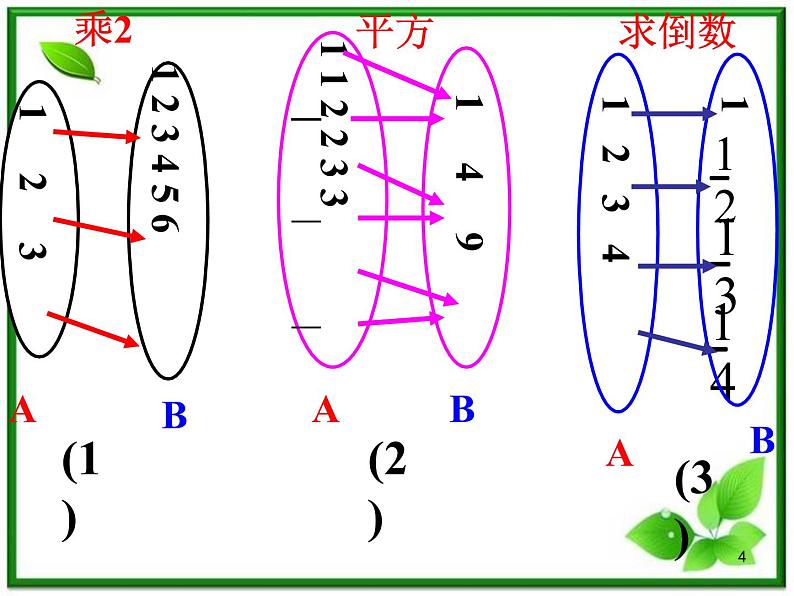
1 1 2 2 3 3
以上三个实例,变量之间的关系有什么共同点?
对于数集A中的每一个 数 ,按照某种对应关系 f ,在数集B中都有唯一确定的值和它对应,
设A,B是非空的数集,如果按照某种确定对应关系 f,对于集合A中的任意一个数x,在集合B中都有唯一确定的数 f (x)和它对应,那么就称f:A→B 为从集合A到集合B的一个函数.记作
③集合A中数的任意性,集合B中数的唯一性;
⑥ f 表示对应关系,不同函数中f 的具 体含义不一样;
⑤函数符号y=f (x) 表示y是x的函数, f (x)不是表示 f 与x的乘积;
说明: ①A,B是非空数集;
④方向性:f:A →B
可以是解析式,可以是图像,可以是表格
注:值域是由定义域和对应关系共同确定的
下列图象是函数图象吗?
1,判断下列对应是否为从集合A到集合B的函数。
判断一个对应关系是否是函数的方法:
1.定义法:对于定义域内的每一个数,若有唯一的一个函数值与之对应则是函数
2.图像法:在定义域内,对任意一个数,过它做x轴的垂线,若垂线与y轴有且只有一个交点,则是函数,否则不是
设A,B是非空的数集,如果按照某种确定对应关系 f,对于集合A中的任意一个数x,在集合B中都有唯一确定的数 f (x)和它对应,那么就称f:A→B 为从集合A到集合B的一个函数.记作 ,其中x 叫做自变量.
3.区间不能表示单元素集
4.区间不能表示不连续的数集
1.区间(a,b),必须有b>a
练习:用区间表示下列集合:
从图像读函数的定义域和值域
P25 B组第一题:
解(1) 有意义的实数x的集合是{x|x≥-3} 有意义的实数x的集合是{x|x≠-2} 所以 这个函数的定义域就是
分 析:函数的定义域通常由问题的实际背景确定. 如果只给出解析式 y=f(x),而没有指明它的定义域,那么函数的定义域就是指能使这个式子有意义的实数x的集合.
例3. 求下列函数的定义域
如果两个函数的定义域和对应关系都相同的时候,则这两个函数相等
例2.下列函数哪个与函数y=x相等?
(2) 这个函数和y=x (x∈R) 对应关系一样 ,定义域相同x∈R,所以它和y=x (x∈R)相等.
(3) 这个函数和y=x(x∈R)
定义域相同x ∈R,但是当x<0时,它的对应关系为y=-x所以它和y=x(x∈R)不相等.
例5:已知f(x)=x2+a,求f[f(x)]
变式:已知f(x)=x2+a,g(x)=2x+b,若 f[g(x)]=4x2+8x+5,求a,b
4.函数y=f(x)的定义域为[-1,1],若k∈(0,1),则F(x)=f(x-k)+f(x+k)的定义域是
5.已知f(x)=(x+m)2,g(x)=2x+n,若 g[f(x)]=2x2+4x+3,求m,n
沪教版高中一年级 第一学期3.1函数的概念教课ppt课件: 这是一份沪教版高中一年级 第一学期3.1函数的概念教课ppt课件,共17页。
高中数学沪教版高中一年级 第一学期3.1函数的概念评课课件ppt: 这是一份高中数学沪教版高中一年级 第一学期3.1函数的概念评课课件ppt,共14页。PPT课件主要包含了知识巩固,函数的定义,值域是集合B的子集,函数的三要素,知识探究,例题讲解,A0个,B1个,C2个,D3个等内容,欢迎下载使用。
沪教版高中一年级 第一学期3.1函数的概念集体备课ppt课件: 这是一份沪教版高中一年级 第一学期3.1函数的概念集体备课ppt课件,共40页。PPT课件主要包含了不等于零,大于或等于0,xx≠0,yy≠0,yy0,-11,求函数的定义域,求已知函数的值域等内容,欢迎下载使用。













