高中数学沪教版高中一年级 第一学期2.5不等式的证明学案设计
展开
这是一份高中数学沪教版高中一年级 第一学期2.5不等式的证明学案设计,共9页。
§2.1.1不等式的的证明(1)比较法 ☆学习目标: 1. 理解并掌握证明不等式的基本方法---比较法; 2. 了解琴生不等式的及其背景☻知识情景: 1.绝对值三角不等式: 定理1 如果, 那么. 当 且仅当 时, 等号成立. 定理2 如果, 那么. 当且仅当 时, 等号成立.2. 含绝对值不等式的解法:设为正数, 则 10.; 20.;30. 设, 则.3.实数大小必较法则: ☆案例学习: 例1 设,求证:. 例2 若实数,求证: 例3已知求证 例4 甲、乙两人同时同地沿同一路线走到同一地点。甲有一半时间以速度行走,另一半时 间以速度行走;乙有一半路程以速度行走,另一半路程以速度行走. 如果, 问甲、乙两人谁先到达指定地点. 例5 设 求证;对任意实数,恒有 “欲穷千里目,更上一层楼.” 10. 在例5中, 特别地, 令 , 则得 再结合函数的图象, 这数和形 20.琴生在1905年给出了一个定义:设函数定义域为,如果,都有 (1)则称为上的下凸函数. 若把(1)式的不等号反向,则称为上的 函数 30. 其推广形式是:若函数的是上的下凸函数,则,都有 (2) 当且仅当时等号成立. 一般称(2)式为琴生不等式. 40.琴生不等式推广形式:设,是上的下凸函数, 则 都有:, 当且仅当时 .若是上凹函数,则上述不等式反向. 把琴生不等式应用于一些具体的函数,可以推出许多著名不等式. 选修4-5练习 §2.1.1不等式的的证明(1)比较法 姓名 1、比较下面各题中两个代数式值的大小:(1)与; (2)与. 2、已知 求证:(1) (2) 3、若,求证 4、已知a≠0,比较与的大小. 5、(上海)已知函数=+有如下性质: 如果常数>0,那么该函数在0,上是减函数,在,+∞上是增函数.(1)如果函数=+(>0)的值域为6,+∞,求的值;(2)研究函数=+(常数>0)在定义域内的单调性,并说明理由;(3)对函数=+和=+(常数>0)作出推广,使它们都是你所推广的函 数的特例.研究推广后的函数的单调性(只须写出结论,不必证明),并求函数= +(是正整数)在区间[,2]上的最大值和最小值(可利用你的研究结论). 6、(山东)已知函数,其中,为常数.(Ⅰ)当时,求函数的极值;(Ⅱ)当时,证明:对任意的正整数,当时,有. 参考答案:例3本题可以尝试使用差值比较和商值比较两种方法进行。 证明:1) 差值比较法:注意到要证的不等式关于对称,不妨设,从而原不等式得证。2)商值比较法:设 故原不等式得证。注:比较法是证明不等式的一种最基本、最重要的方法。用比较法证明不等式的步骤是: 作差(或作商)、变形、判断符号。例4分析:设从出发地点至指定地点的路程是,甲、乙两人走完这段路程所用的时间分别为。 要回答题目中的问题,只要比较的大小就可以了。解:设从出发地点至指定地点的路程是,甲、乙两人走完这段路程所用的时间分别为,根据题意有,,可得,,从而,其中都是正数,且。于是,即。从而知甲比乙首先到达指定地点。讨论:如果,甲、乙两人谁先到达指定地点? 例5证明 考虑(1)式两边的差。 == (2) 即(1)成立。5、(上海)(本题满分18分,本题共有3个小题,第1小题满分3分,第2小题满分6分,第3小题满分9分)已知函数=+有如下性质:如果常数>0,那么该函数在0,上是减函数,在,+∞上是增函数.(1)如果函数=+(>0)的值域为6,+∞,求的值;(2)研究函数=+(常数>0)在定义域内的单调性,并说明理由;(3)对函数=+和=+(常数>0)作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明),并求函数=+(是正整数)在区间[,2]上的最大值和最小值(可利用你的研究结论).[解](1)函数y=x+(x>0)的最小值是2,则2=6, ∴b=log29. (2) 设0<x1<x2,y2-y1=. 当<x1<x2时, y2>y1, 函数y=在[,+∞)上是增函数; 当0<x1<x2<时y2<y1, 函数y=在(0,]上是减函数. 又y=是偶函数,于是,该函数在(-∞,-]上是减函数, 在[-,0)上是增函数; (3)可以把函数推广为y=(常数a>0),其中n是正整数. 当n是奇数时,函数y=在(0,]上是减函数,在[,+∞) 上是增函数, 在(-∞,-]上是增函数, 在[-,0)上是减函数; 当n是偶数时,函数y=在(0,]上是减函数,在[,+∞) 上是增函数, 在(-∞,-]上是减函数, 在[-,0)上是增函数; F(x)=+ = 因此F(x) 在 [,1]上是减函数,在[1,2]上是增函数. 所以,当x=或x=2时,F(x)取得最大值()n+()n; 当x=1时F(x)取得最小值2n+1;6. 已知函数其中n∈N*,a为常数.(Ⅰ)当n=2时,求函数f(x)的极值;(Ⅱ)当a=1时,证明:对任意的正整数n, 当x≥2时,有f(x)≤x-1.(Ⅰ)解:由已知得函数f(x)的定义域为{x|x>1}, 当n=2时, 所以 (1)当a>0时,由f(x)=0得>1,<1,此时 f′(x)=.当x∈(1,x1)时,f′(x)<0,f(x)单调递减;当x∈(x1+∞)时,f′(x)>0, f(x)单调递增.(2)当a≤0时,f′(x)<0恒成立,所以f(x)无极值.综上所述,n=2时,当a>0时,f(x)在处取得极小值,极小值为当a≤0时,f(x)无极值.(Ⅱ)证法一:因为a=1,所以 当n为偶数时,令则 g′(x)=1+>0(x≥2).所以当x∈[2,+∞]时,g(x)单调递增,又 g(2)=0, 因此≥g(2)=0恒成立, 所以f(x)≤x-1成立.当n为奇数时, 要证≤x-1,由于<0,所以只需证ln(x-1) ≤x-1, 令 h(x)=x-1-ln(x-1), 则 h′(x)=1-≥0(x≥2), 所以 当x∈[2,+∞]时,单调递增,又h(2)=1>0, 所以当x≥2时,恒有h(x) >0,即ln(x-1)<x-1命题成立.综上所述,结论成立.证法二:当a=1时, 当x≥2时,对任意的正整数n,恒有≤1, 故只需证明1+ln(x-1) ≤x-1. 令 则 当x≥2时,≥0,故h(x)在上单调递增, 因此 当x≥2时,h(x)≥h(2)=0,即1+ln(x-1) ≤x-1成立. 故 当x≥2时,有≤x-1. 即f(x)≤x-1.
相关学案
这是一份高中数学沪教版高中一年级 第一学期2.5不等式的证明导学案,共6页。学案主要包含了选择,填空,解答等内容,欢迎下载使用。
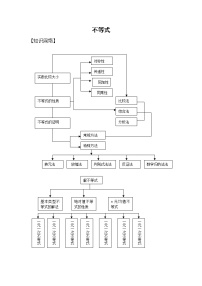
这是一份沪教版高中一年级 第一学期2.5不等式的证明学案,共31页。学案主要包含了知识网络,考点透视,典例精析,常见误区,基础演练等内容,欢迎下载使用。
这是一份高中数学沪教版高中一年级 第一学期2.5不等式的证明学案及答案,共5页。