高中数学沪教版高中一年级第二学期6.5最简三角方程教学设计

展开

这是一份高中数学沪教版高中一年级第二学期6.5最简三角方程教学设计，共25页。

上海市零陵中学胡化平
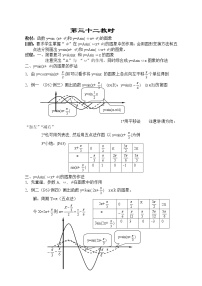
函数y=Asinx，xR(A>0且A1)的图像可以看作把函数y=sinx，xR的图像上的所有点的纵坐标伸长(A>1)或缩短(0 函数y=sinωx, xR (ω>0且ω1)的图像，可看作把函数y=sinx，xR的图像上所有点的横坐标缩短(ω>1)或伸长(0<ω<1)到原来的ω倍（纵坐标不变）．若ω<0则可用诱导公式将符号“提出”再作图ω决定了函数的周期
引例1：画出函数的图像
(1)函数y＝sin(x＋ )的图像可看作把y=sinx图像上所有的点向左平行移动个单位长度而得到
(2)函数y＝sin(x－ )的图像可看作把y=sinx图像上所有点向右平行移动个单位长度而得到
A ：称为振幅；T＝：称为周期；f＝：称为频率；ωx＋：称为相位,x＝0时的相位称为初相
途径一：先平移变换再周期变换(伸缩变换) 先将y＝sinx的图像向左( ＞0)或向右( ＜0)平移｜｜个单位，再将图像上各点的横坐标变为原来的倍(ω＞0)，便得y＝sin(ωx＋ )的图像
途径二：先周期变换(伸缩变换)再平移变换先将y＝sinx的图像上各点的横坐标变为原来的倍(ω＞0),再沿x轴向左( ＞0)或向右( ＜0)平移个单位，便得y＝sin(ωx＋ )的图像
例1：已知如图是函数y＝2sin(ωx＋ )其中｜｜＜的图像，那么( )Aω＝，＝ Bω＝，＝-Cω＝2，＝ Dω＝2，＝-
例2已知函数y＝Asin(ωx＋ )在同一周期内，当x＝时函数取得最大值2，当x＝时函数取得最小值－2，则该函数的解析式为( )A.y＝2sin(3x－ ) B.y＝2sin(3x＋ )C.y＝2sin( ＋ ) D.y＝2sin( － )
[说明]：由y＝Asin(ωx＋ )的图像求其函数式：一般来说，在这类由图像求函数式的问题中，如对所求函数式中的A、ω、不加限制(如A、ω的正负，角的范围等)，那么所求的函数式应有无数多个不同的形式(这是由于所求函数是周期函数所致)，因此这类问题多以选择题的形式出现，我们解这类题的方法往往因题而异，但逆用“五点法”作图的思想却渗透在各不同解法之中。
巩固练习《课本》P102-103 2,3,4 P105 1,2,3
课堂小结：本节课主要研究了由y＝sinx的图像变换出y＝Asin(ωx＋ )的图像的过程中的平移变换，及三个变换相互关系，它们的规律可概括如下：