高中数学湘教版必修37.5空间直角坐标系评课ppt课件

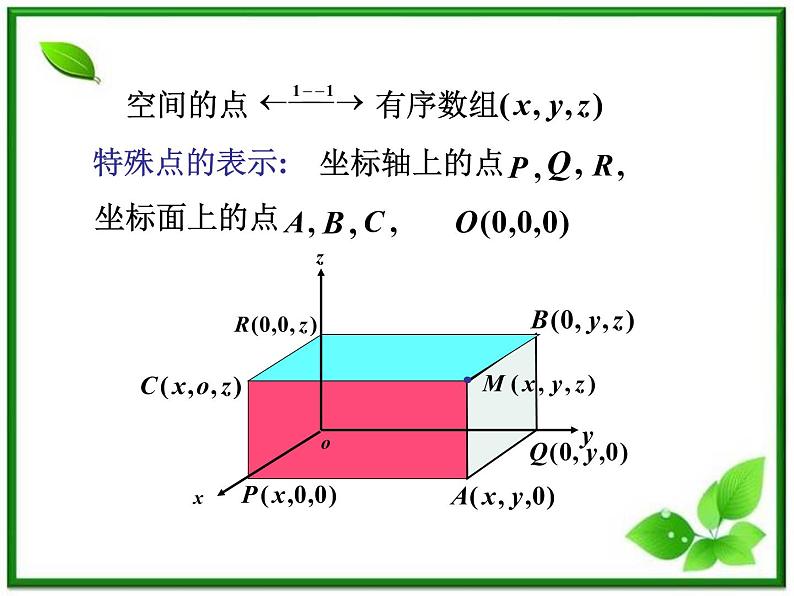
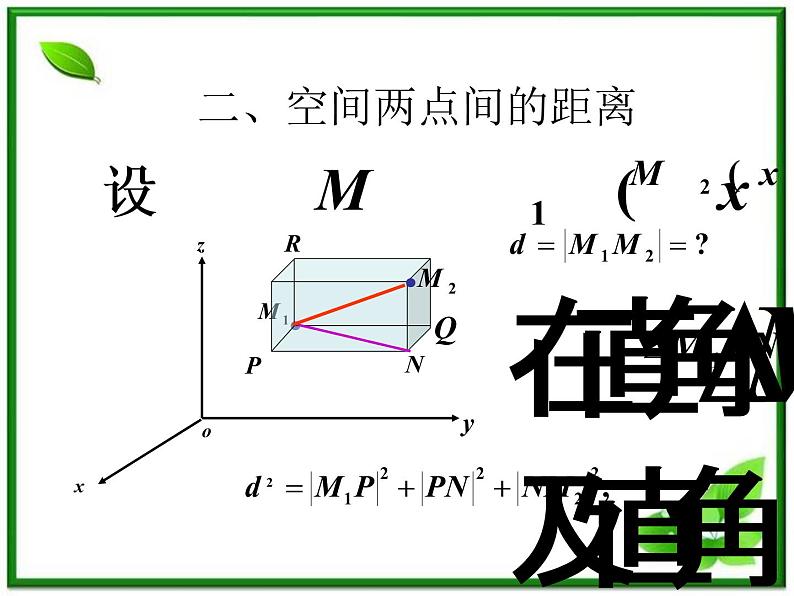
这是一份高中数学湘教版必修37.5空间直角坐标系评课ppt课件，共60页。PPT课件主要包含了空间直角坐标系，空间点的直角坐标，空间的点，特殊点的表示，空间两点间的距离，特殊地若两点分别为，原结论成立，设P点坐标为，所求点为，空间两点间距离公式等内容，欢迎下载使用。
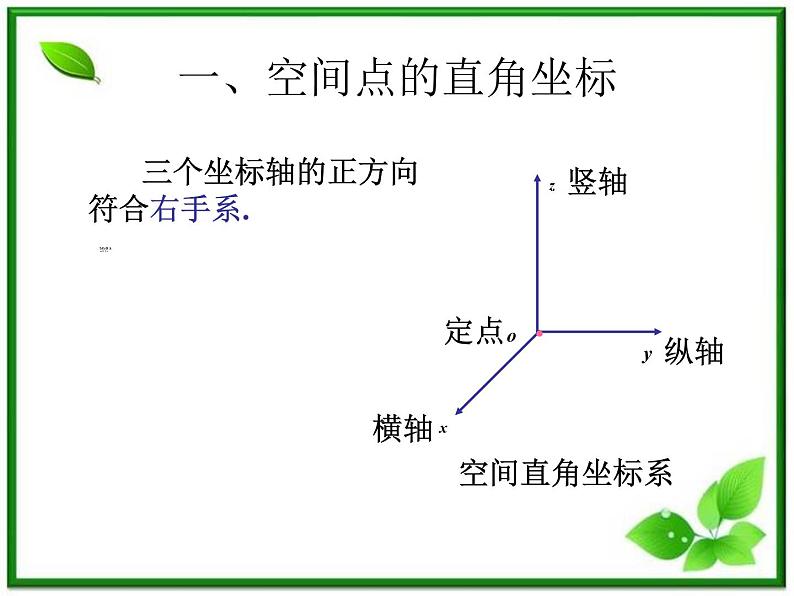
三个坐标轴的正方向符合右手系.
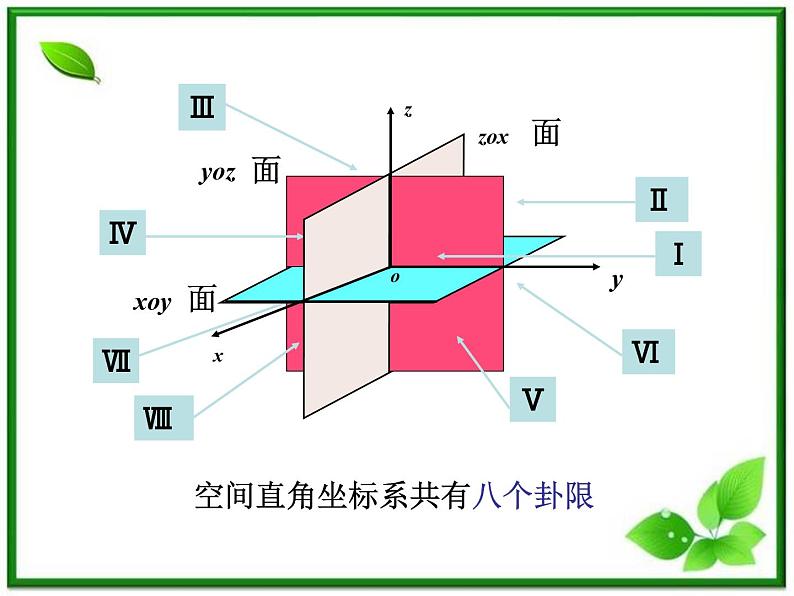
空间直角坐标系共有八个卦限
（注意它与平面直角坐标系的区别）
在空间直角坐标系中，指出下列各点在哪个卦限？
A:Ⅳ; B:Ⅴ; C:Ⅷ; D:Ⅲ;
1、下列各点所在象限分别是：
一、函数的平均值
第二节 向量及其加减法 向量与数的乘法
一、向量的概念二、向量的加减法三、向量与数的乘法四、小结 思考题
既有大小又有方向的量.
不考虑起点位置的向量.
大小相等且方向相同的向量.
大小相等但方向相反的向量.
（平行四边形法则有时也称为三角形法则）
向量的加法符合下列运算规律：
数与向量的乘积符合下列运算规律：
按照向量与数的乘积的规定，
上式表明：一个非零向量除以它的模的结果是一个与原向量同方向的单位向量.
例2 试用向量方法证明：对角线互相平分的四边形必是平行四边形.
已知平行四边形ABCD的对角线
试用 表示平行四边形四边上对应的向量.
第三节 向量的坐标
一、向量在轴上的投影与投影定理二、向量在坐标轴上的分向量与向量三、向量的模与方向余弦的坐标表示式四、小结 思考题
一、向量在轴上的投影与投影定理
空间两向量的夹角的概念：
类似地，可定义向量与一轴或空间两轴的夹角.
空间一向量在轴上的投影
关于向量的投影定理（1）
(4) 相等向量在同一轴上投影相等；
关于向量的投影定理（2）
二、向量在坐标轴上的分向量与向量
按基本单位向量的坐标分解式：
在三个坐标轴上的分向量：
向量的加减法、向量与数的乘法运算的坐标表达式
非零向量与三条坐标轴的正向的夹角称为方向角.
三、向量的模与方向余弦的坐标表示式
方向余弦通常用来表示向量的方向.
向量方向余弦的坐标表示式
特殊地：单位向量的方向余弦为
向量在轴上的投影与投影定理.
向量在坐标轴上的分向量与向量的坐标.
向量的模与方向余弦的坐标表示式.
（注意分向量与向量的坐标的区别）
第四节 数量积 向量积 混合积
一、两向量的数量积二、两向量的向量积三、向量的混合积四、小结 思考题
两向量作这样的运算, 结果是一个数量.
数量积也称为“点积”、“内积”.
结论 两向量的数量积等于其中一个向量的模和另一个向量在这向量的方向上的投影的乘积.
数量积符合下列运算规律：
两向量夹角余弦的坐标表示式
由此可知两向量垂直的充要条件为
向量积也称为“叉积”、“外积”.
向量积符合下列运算规律：
向量积还可用三阶行列式表示
（1）向量混合积的几何意义：
式中正负号的选择必须和行列式的符号一致.
（注意共线、共面的条件）
第五节 曲面及其方程
一、曲面方程的概念二、旋转曲面三、柱面四、小结 思考题
水桶的表面、台灯的罩子面等．
曲面在空间解析几何中被看成是点的几何轨迹．
以下给出几例常见的曲面.
特殊地：球心在原点时方程为
例4 方程 的图形是怎样的？
图形上不封顶，下封底．
以上几例表明研究空间曲面有两个基本问题：
（2）已知坐标间的关系式，研究曲面形状．
（讨论柱面、二次曲面）
（1）已知曲面作为点的轨迹时，求曲面方程．
以一条平面曲线绕其平面上的一条直线旋转一周所成的曲面称为旋转曲面.
这条定直线叫旋转曲面的轴．
将 代入
例6 将下列各曲线绕对应的轴旋转一周，求生成的旋转曲面的方程．
从柱面方程看柱面的特征：
椭圆柱面 // 轴
双曲柱面 // 轴
抛物柱面 // 轴
旋转曲面的概念及求法.
柱面的概念(母线、准线).
指出下列方程在平面解析几何中和空间解析几何中分别表示什么图形？
第六节 空间曲线及其方程
一、空间曲线的一般方程二、空间曲线的参数方程三、空间曲线在坐标面上的投影四、小结 思考题
曲线上的点都满足方程，满足方程的点都在曲线上，不在曲线上的点不能同时满足两个方程.
空间曲线C可看作空间两曲面的交线.
一、空间曲线的一般方程
例1 方程组 表示怎样的曲线？
例2 方程组 表示怎样的曲线？
二、空间曲线的参数方程
动点从A点出发，经过t时间，运动到M点
螺旋线的参数方程还可以写为
上升的高度与转过的角度成正比．即
设空间曲线的一般方程：
以此空间曲线为准线，垂直于所投影的坐标面.
三、空间曲线在坐标面上的投影
如图:投影曲线的研究过程.
类似地：可定义空间曲线在其他坐标面上的投影
例4 求曲线 在坐标面上的投影.
补充: 空间立体或曲面在坐标面上的投影.
空间曲线的一般方程、参数方程．
空间曲线在坐标面上的投影．
第七节 平面及其方程
一、平面的点法式方程二、平面的一般方程三、两平面的夹角四、小结 思考题
如果一非零向量垂直于一平面，这向量就叫做该平面的法线向量．
垂直于平面内的任一向量．
平面上的点都满足上方程，不在平面上的点都不满足上方程，上方程称为平面的方程，平面称为方程的图形．
平面一般方程的几种特殊情况：
由所求平面与已知平面平行得
（向量平行的充要条件）
两平面法向量之间的夹角称为两平面的夹角.
按照两向量夹角余弦公式有
例6 研究以下各组里两平面的位置关系：
（熟记平面的几种特殊位置的方程）
（注意两平面的位置特征）
第八节 空间直线及其方程
一、空间直线的一般方程二、空间直线的对称式方程与参数方程三、两直线的夹角四、直线与平面的夹角五、小结 思考题
空间直线可看成两平面的交线．
一、空间直线的一般方程
如果一非零向量平行于一条已知直线，这个向量称为这条直线的方向向量．
二、空间直线的对称式方程与参数方程
方向向量的余弦称为直线的方向余弦.
例1 用对称式方程及参数方程表示直线
因所求直线与两平面的法向量都垂直
两直线的方向向量的夹角称之.（锐角）
设所求直线的方向向量为
再求已知直线与该平面的交点N,
代入平面方程得 ,
取所求直线的方向向量为
直线与平面的位置关系：
空间直线的对称式方程与参数方程.
（注意两直线的位置关系）
（注意直线与平面的位置关系）
一、基本内容二、小结 思考题
三元二次方程所表示的曲面称之．
相应地平面被称为一次曲面．
讨论二次曲面性状的截痕法：
用坐标面和平行于坐标面的平面与曲面相截，考察其交线（即截痕）的形状，然后加以综合，从而了解曲面的全貌．
以下用截痕法讨论几种特殊的二次曲面．
椭球面与三个坐标面的交线：
椭圆截面的大小随平面位置的变化而变化.
椭球面的几种特殊情况：
旋转椭球面与椭球面的区别：
原点也叫椭圆抛物面的顶点.
与平面 的交线为椭圆.
与平面 的交线为抛物线.
椭圆抛物面的图形如下：
特殊地：当 时，方程变为
与平面 的交线为椭圆.
截得中心在原点的双曲线.
平面 的截痕是两对相交直线.
椭球面、抛物面、双曲面、截痕法.
（熟知这几个常见曲面的特性）